Обучение и трудоустройство Java-программистов от Junior до Senior
Битовые операции в Java.
Автор: Андрей Самойлов
- Главная
- Статьи
Java позволяет манипулировать числами на битовом уровне, что означает работу с битами, из которых состоит число, а именно с его представлением в двоичной системе счисления. Что же такое система счисления вообще и двоичная система в частности?
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Количество цифр, используемых в системе счисления, называется её «основанием».
Позиционные системы счисления — это системы счисления,
в которых значение цифры напрямую зависит от её положения в числе.
Двоичная система счисления — позиционная система счисления с основанием 2. В двоичной системе счисления числа записываются с помощью двух символов (0 и 1).
Двоичная арифметика.
Таблица сложения
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10(перенос в старший разряд) |
Таблица вычитания
| — | 0 | 1 |
|---|---|---|
| 0 | 0 | д |
| 1 | (заём из старшего разряда) 1 |
0 |
Пример сложения «столбиком» (1410 + 510 = 1910 или 11102 + 1012 = 100112):
| + | 1 | 1 | 1 | 0 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
| × | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Пример умножения «столбиком» (1410 * 510 = 7010 или 11102 * 1012 = 10001102):
| × | 1 | 1 | 1 | 0 | |||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
Эти операции работают с целочисленными типами данных
| Тип | Размер (бит) | Диапазон |
|---|---|---|
| byte | 8 бит | от -128 до 127 |
| short | 16 бит | от -32768 до 32767 |
| char | 16 бит | от 0 до 65535 |
| int | 32 бит | от -2147483648 до 2147483647 |
| long | от -9223372036854775808 до +9223372036854775807 |
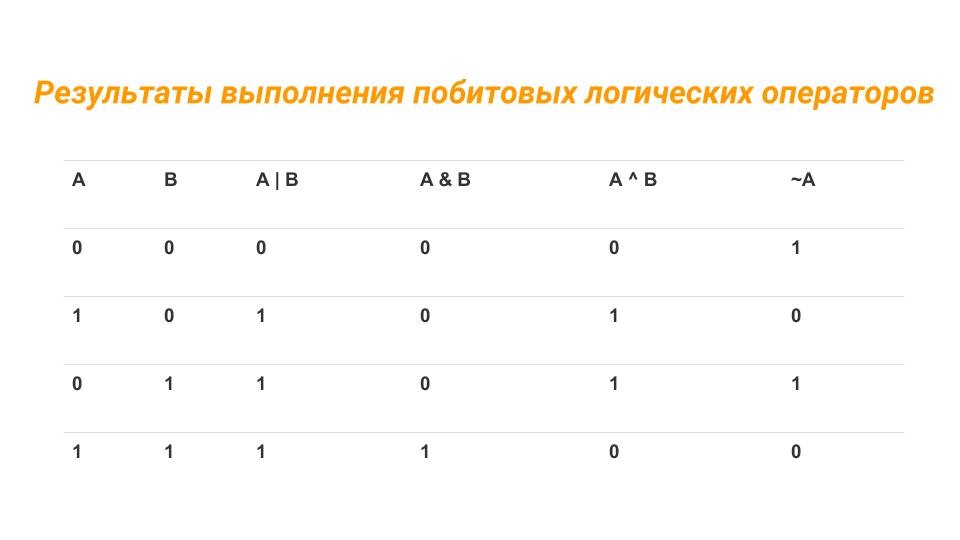
Таблица истинности побитовых операций выглядит следующим образом
| A | B | A & B | A | B | A ^ B |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
Первые четыре оператора представляют собой применение битовых масок к аргументу в соответствие
с логическими функциями.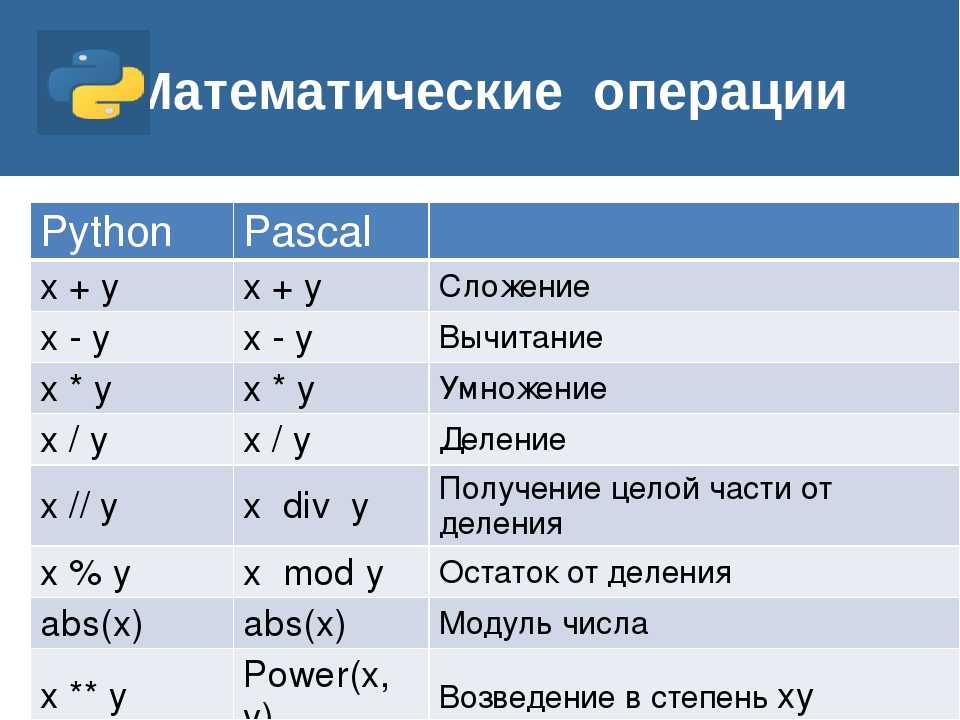 Например, оператор & применяется для поиска элемента в HashMap по формуле
h & (length -1), где h — хэшкод элемента, а length — длина массива
Например, оператор & применяется для поиска элемента в HashMap по формуле
h & (length -1), где h — хэшкод элемента, а length — длина массива
Наибольший интерес представляют операторы сдвига. Первым операндом оператора сдвига является число, которое нужно обработать, а вторым — количество бит, на которое следует выполнить сдвиг. Результатом операции сдвига является двоичное представление числа, сдвинутое в заданном направлении. Знаковые сдвиги также называют арифметическими, а беззнаковые — логическими.
Представление отрицательных чисел в Java.
Для хранения отрицательных чисел используется дополнительный код или второе дополнение (two’s complement). Положительное число преобразуется в отрицательное число путём инвертирования его бит с добавлением единицы.
Пример: Преобразование 32-битного числа 5 = 101:
Исходное число: 0000 0000 0000 0000 0000 0000 0000 0101
Инвертируем: 1111 1111 1111 1111 1111 1111 1111 1010
Прибавляем 1: 0000 0000 0000 0000 0000 0000 0000 0001
Результат: 1111 1111 1111 1111 1111 1111 1111 1011
Знаковый сдвиг влево (
Сдвигает двоичное представление первого операнда влево на количество бит,
заданное во втором операнде, знак числа сохраняется. Младшие(крайние правые) биты при этом заполняются нулями.
Соответствует умножению на 2.
Младшие(крайние правые) биты при этом заполняются нулями.
Соответствует умножению на 2.
Примеры:
27 (11011)
-5 (11111111111111111111111111111011)
Если число выходит за границы диапазона типа int, крайний бит теряется:
2 147 483 647 (1111111111111111111111111111111)
Почему не существует беззнакового(логического) сдвига влево? Потому что такой сдвиг не оказывает влияния на старший значащий бит(MSB) — крайний левый бит числа, изменяются только крайние правые биты. Кроме того, в процессорах семейства 8086 арифметический и логический сдвиг выполняют одну и ту же операцию.
Знаковый сдвиг вправо (>>)
Сдвигает двоичное представление первого операнда вправо на количество бит,
заданное во втором операнде, знак числа сохраняется. Старшие(крайние левые биты) заполняются нулями. Соответствует делению на 2:
Соответствует делению на 2:
24 (11000) >> 1 = 12 (1100)
-4 (11111111111111111111111111111100) >> 1 = -2 (11111111111111111111111111111110)
Беззнаковый сдвиг вправо(>>>)
Сдвигает двоичное представление первого операнда вправо на количество бит, заданное во втором операнде, знак числа не сохраняется. Для положительных чисел работает как деление:
24 (11000) >>> 1 = 12 (1100)
-24 (1111 1111 1111 1111 1111 1111 1110 1000) >>> 1 = 2147483636 (0111 1111 1111 1111 1111 1111 1111 0100)
Можно увидеть, что знаковый бит был заменён нулём
Особенности работы операторов сдвига
Операторы сдвига всегда возвращают тип int, даже если аргумент типа, например, byte. поэтому следующий код вернёт ошибку:
byte n = 27;
n = n
java: possible loss of precision
required: byte
ound: int
Устранить ошибку можно путём приведения к типу byte:
n = (byte) (n
Нельзя сдвинуть на количество бит, большее, чем разрядность операнда. При этом происходит неявное сокращение правого (кол-во бит) операнда.
При этом происходит неявное сокращение правого (кол-во бит) операнда.
Пример:
Если сдвинуть данное число на 32 бита, по идее, результат должен состоять из одних нулей, но на самом деле это не так:
-1 (11111111111111111111111111111111) >> 32 = -1 (11111111111111111111111111111111)
-1(11111111111111111111111111111111) >>> 32 = -1 (11111111111111111111111111111111)
Примеры применения битовых операций
- Ускорение операций умножения и деления чисел на два. Примеры можно увидеть в стандартной библиотеке jdk.
- Битовые поля(флаги). Пример пусть есть права на доступ — чтение, запись, выполнение. Их удобнее хранить не в трёх разных переменных, а в одной, устанавливая соответствующие биты.
- Алгоритмы шифрования и сжатия (например, Шифр Вернама построен на XOR).
- Работа с графикой.
- Работа с сетью.
 y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}
y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}что это такое простыми словами в языке Ассемблер
Битовая маска — это двоичное число, которое нужно для получения определенных цифр из другого двоичного числа. С помощью специальных логических операций число сравнивают с маской и получают результат — значение конкретного бита или битов, то есть цифру.
Битовые маски требуются для работы с двоичными числами, в которых хранится массив булевых значений. Булево значение — логическое, оно может быть равно 1 или 0, где 1 — это «да», а 0 — это «нет». Поэтому хранить такие значения в виде длинных двоичных чисел разумно.
 А чтобы получить из последовательности конкретное значение, нужна маска — двоичное число, которое «высвечивает» из массива нужный бит.
А чтобы получить из последовательности конкретное значение, нужна маска — двоичное число, которое «высвечивает» из массива нужный бит.Битовые строки нужны для хранения большого количества булевых значений. Одно двоичное число или булево значение занимает один бит. Если создать для него целую переменную, потратится как минимум байт, то есть восемь бит. А если хранить все в виде одного числа, в восьми битах удастся уместить восемь значений, то есть в восемь раз больше. Каждому биту будет соответствовать свое значение. Такой способ хранения позволяет оптимизировать код.
Хранение свойств объектов. Битовые маски бывают нужны при работе с объектами, у которых много свойств, в том числе тех, которые можно представить в виде булевых значений. Свойства хранятся в виде двоичных строк, маска нужна для получения значения определенного свойства.
Курс Уверенный старт в IT Поможем определить подходящую вам IT-профессию и освоить её с нуля.
 Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности.
Хочу в IT!
Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности.
Хочу в IT!Динамическое программирование. Это способ решения сложных задач: они декомпозируются на маленькие и решаются поэтапно. Программа формируется так, чтобы каждая маленькая подзадача решалась только один раз, а потом исполнение переходило на другую.
Обычно динамическое программирование используют для задач, связанных с графами и траекториями. Например, с помощью ДП на битовых масках можно написать решение знаменитой задачи коммивояжера — сложного задания на поиск оптимальной траектории.
Ассемблер. Язык ассемблера — это низкоуровневый язык, который переводится в машинные коды. На нем обычно пишут системные программисты, специалисты, которые работают с «железом», создают драйверы и подобное программное обеспечение.

На низком уровне важно сохранение каждого бита, поэтому информация хранится в виде битовых строк — выделять целый байт на одно логическое значение нерационально. Логических значений на близком к «железу» уровне много: это сигналы на входах процессора, наличие значения в том или ином регистре и так далее. Данные надо не только хранить, и получать. Поэтому маски в подобных задачах используются часто.
Работа с сетью.
Битовые маски бывают нужны при расчете контрольных сумм и в других ситуациях, где важна экономия памяти.
Хранение. Например, есть три вопроса и ответы на них.
 Если на первый и второй вопросы ответы даны правильный, а на третий — неверно, получится список значений формата «правда, правда, ложь». Это булевы значения. В двоичном представлении их можно отобразить как 110, это число и есть битовая строка.
Если на первый и второй вопросы ответы даны правильный, а на третий — неверно, получится список значений формата «правда, правда, ложь». Это булевы значения. В двоичном представлении их можно отобразить как 110, это число и есть битовая строка.Плюс такого представления в том, что место для записи экономится, а последовательность значений не теряется благодаря разрядности. Если мы посмотрим на строку, то с легкостью можем ответить, на какие именно вопросы был дан правильный ответ.
Маскирование. Компьютер воспринимает информацию иначе. Ему нельзя сказать: «Посмотри на первый бит и выдай его значение» — нужно использовать маску. Например, чтобы узнать, какой ответ был дан на второй вопрос, потребуется маска 010 — единица стоит в том бите, значение которого мы хотим получить. А затем нужно применить побитовую операцию сложения — о ней мы подробнее поговорим ниже.
Побитовые операции.
 Работать с масками можно благодаря побитовым операциям — они попарно сравнивают конкретные биты двух чисел и применяют к ним логические операции. Первый бит одного числа сравнится с первым битом другого, второй — со вторым, и так далее. Это похоже на сложение и вычитание в столбик, когда человек работает с цифрами попарно. Только вместо сложения и вычитания — логические операции. Они возвращают 1 или 0 в зависимости от результатов сравнения.
Работать с масками можно благодаря побитовым операциям — они попарно сравнивают конкретные биты двух чисел и применяют к ним логические операции. Первый бит одного числа сравнится с первым битом другого, второй — со вторым, и так далее. Это похоже на сложение и вычитание в столбик, когда человек работает с цифрами попарно. Только вместо сложения и вычитания — логические операции. Они возвращают 1 или 0 в зависимости от результатов сравнения.Они могут быть следующими:
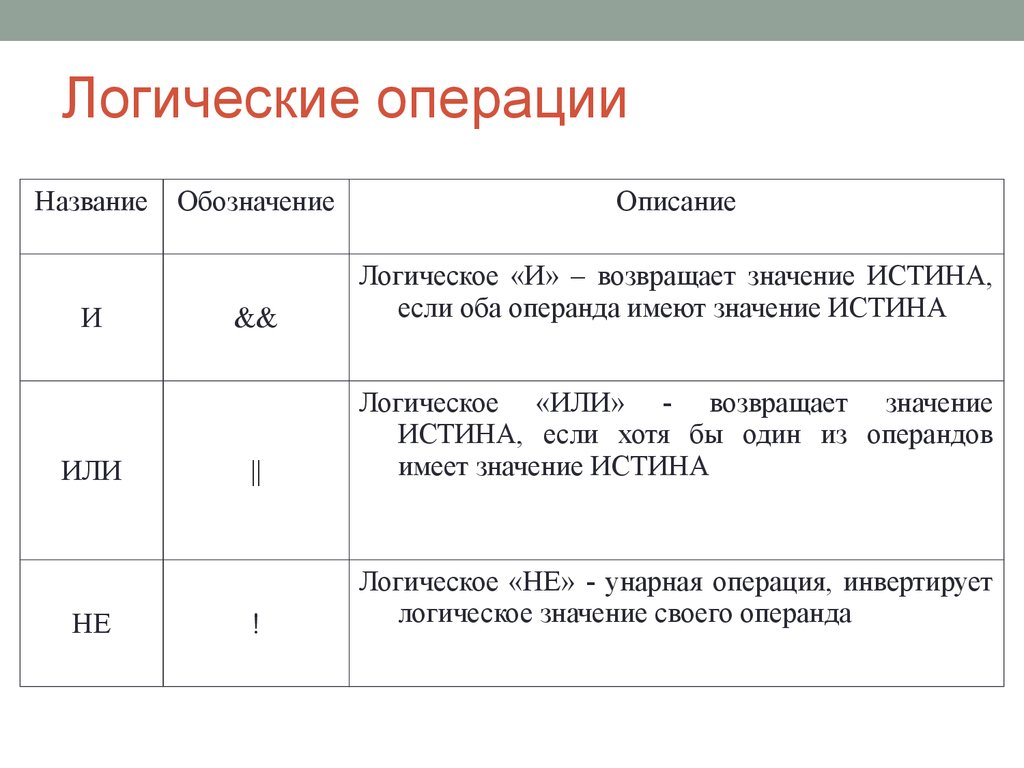
- логическое «И» — дает результат 1, если значения обоих битов равны 1, в остальных случаях 0;
- логическое «ИЛИ» — дает результат 1, если значение хотя бы одного бита равно 1;
- логическое исключающее «ИЛИ» — дает результат 1, если значения разные.
Еще есть логическое «НЕ», которое инвертирует бит, но эта операция, в отличие от предыдущих, унарная — ей нужна не пара битов для сравнения, а один бит для инверсии.

Перечисленные выше логические операции — основной инструмент работы с битовыми масками. Они побитово сравнивают двоичную строку с маской, выдают результат, и этот результат устанавливает, обнуляет или получает конкретное значение.
Установка значения. Происходит с помощью логического «ИЛИ». Если у нас есть строка 1000, и мы хотим установить в первый с конца бит 1, мы пишем маску 0001 и применяем операцию «строка ИЛИ маска», «1000 ИЛИ 0001». Результат побитовой операции — число 1001. Значение добавлено.
Снятие значения. Происходит с помощью исключающего «ИЛИ». Чтобы убрать последнюю единицу из полученного числа, понадобится операция «1001 исключающее ИЛИ 0001». Последняя цифра изменится на 0, потому что значение в строке и значение в маске — одинаковые.
Проверка значения. Происходит с помощью логического «И». Чтобы узнать, какой будет первая слева цифра в нашем числе, нужна маска 1000.
 При побитовой операции «1001 И 1000» результатом будет 1000 — это показывает, что нужный бит равен 1. А при операции «0001 И 1000» получится 0000 — это показывает, что бит равен 0.
При побитовой операции «1001 И 1000» результатом будет 1000 — это показывает, что нужный бит равен 1. А при операции «0001 И 1000» получится 0000 — это показывает, что бит равен 0.Чтобы получить нужный бит, вместе с логическим «И» применяют побитовый сдвиг, когда разряды числа как бы «сдвигают» в сторону, пока нужный не станет первым справа. Биты считаются справа налево, поэтому в числе 1000 бит со значением 1 — четвертый. Мы назвали его первым слева для наглядности.
В целом — в любых, где есть работа с двоичными строками. Но шанс встретить такую задачу, например, во фронтенде, в разы ниже, чем в системном программировании. Чем ниже уровень, то есть чем ближе разработка к «железной» части компьютеров, тем чаще придется работать с битовыми масками. С ними могут столкнуться разработчики на ассемблере, на C/C++ или Java, на других языках, которые используются как системные.
Битовые маски — только один из многочисленных способов использования двоичных чисел.
 Вы можете узнать больше о побитовых операциях и о хранении информации в компьютере — для этого есть туториалы, интернет-статьи, учебники и профессиональные курсы.
Вы можете узнать больше о побитовых операциях и о хранении информации в компьютере — для этого есть туториалы, интернет-статьи, учебники и профессиональные курсы.Курс Уверенный старт в IT Поможем определить подходящую вам IT-профессию и освоить её с нуля. Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности. Хочу в IT!
Побитовые операции. Программирование на C и C++
Побитовые операции — это операции, используемые для выполнения манипуляций над битовыми шаблонами или двоичными числами, которые включают в себя работу с отдельными битами. Это быстрое, простое действие, непосредственно поддерживаемое процессором, используется для управления значениями для сравнений и вычислений.
Основа вычислений
Двоичная цифровая система использует только две цифры — 0 и 1.
 Компьютеры работают в двоичном формате, что означает, что они хранят данные и выполняют вычисления, используя только нули и единицы.
Компьютеры работают в двоичном формате, что означает, что они хранят данные и выполняют вычисления, используя только нули и единицы.Хотя одна бинарная цифра может использоваться для представления True (1) (истина) или False (0) (ложь) в логике, для хранения больших чисел и выполнения сложных функций можно использовать несколько двоичных цифр. Фактически любое число может быть представлено в двоичном формате.
Применение
Побитовые операторы используются в следующих областях:
Коммуникационные стеки, где отдельные биты в заголовке, прикрепленные к данным, несут важную информацию.
Встроенное программное обеспечение для управления различными функциями в чипе и индикации состояния аппаратного обеспечения путем управления отдельными битами аппаратных регистров встроенных микроконтроллеров.
Низкоуровневое программирование для таких приложений, как драйверы устройств, криптографическое программное обеспечение, ПО для декодирования видео, распределители памяти, программное обеспечение для сжатия и графики.

Удобное ведение больших наборов целых чисел в задачах поиска и оптимизации.
Побитовые операции, выполняемые с битовыми флагами, которые могут включать экземпляр типа перечисления для хранения любой комбинации значений, определенных в списке перечислителей.
Побитовые операции — как это работает?
В отличие от обычных логических операторов (например, +, -, *), которые работают с байтами или группами байтов, побитовые операторы могут проверять или устанавливать каждый из отдельных битов в байте. Побитовые операции никогда не вызывают переполнения в ячейках памяти, потому что результат, полученный после выполнения операции, находится в пределах диапазона возможных значений для числового типа.
Побитовые операторы, используемые в семействе языков C (C #, C и C ++):
OR (|) — результат является истиной, если любой из операндов истинен.
AND (&) — результат верен, только если оба операнда верны. Его можно использовать для настройки маски проверки значений определенных битов.
 ) — результат является истиной, только если один из его операндов истинен. Он используется, в основном, для переключения определенных бит. Он также помогает заменять две переменные без использования третьей.
) — результат является истиной, только если один из его операндов истинен. Он используется, в основном, для переключения определенных бит. Он также помогает заменять две переменные без использования третьей.NOT (~) — побитовое дополнение или инверсия. Предоставляет поразрядное дополнение к операнду путем инвертирования его значения, так что все нули превращаются в единицы, а все единицы превращаются в нули.
>> (Right-Shift) и << (Left-Shift) — оператор, который перемещает биты в число позиций, заданных вторым операндом в правом или левом направлении. Операторы сдвига используются для выравнивания битов.
Пример работы
Побитовые операторы — это символы, представляющие действия, которые должны выполняться для отдельных битов. Побитовая операция работает на двухбитовых шаблонах одинаковой длины, позиционируя их отдельные биты:
Логическая операция AND (&) каждой битовой пары приводит к 1 (истине), если первый и второй биты равны 1.
 . Левый сдвиг (<<), правый сдвиг (>>) и правый сдвиг нулевой заливки (>>>>) иногда упоминаются как побитовые операторы и называются операторами сдвига бит.
. Левый сдвиг (<<), правый сдвиг (>>) и правый сдвиг нулевой заливки (>>>>) иногда упоминаются как побитовые операторы и называются операторами сдвига бит.Приоритезация
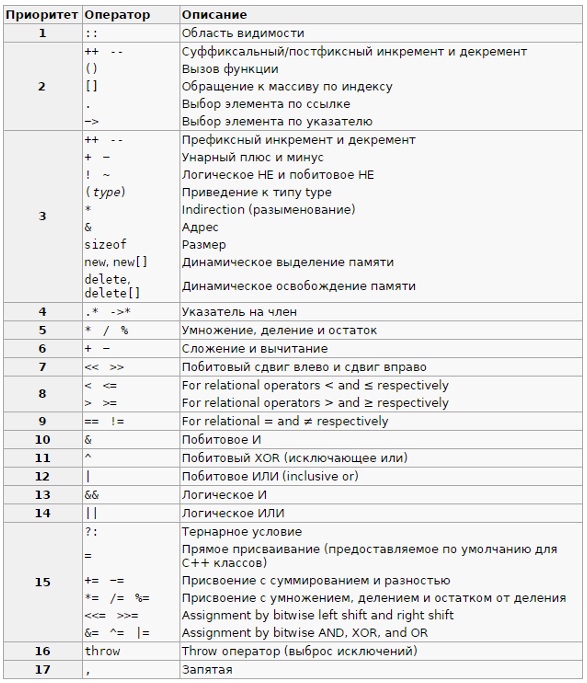
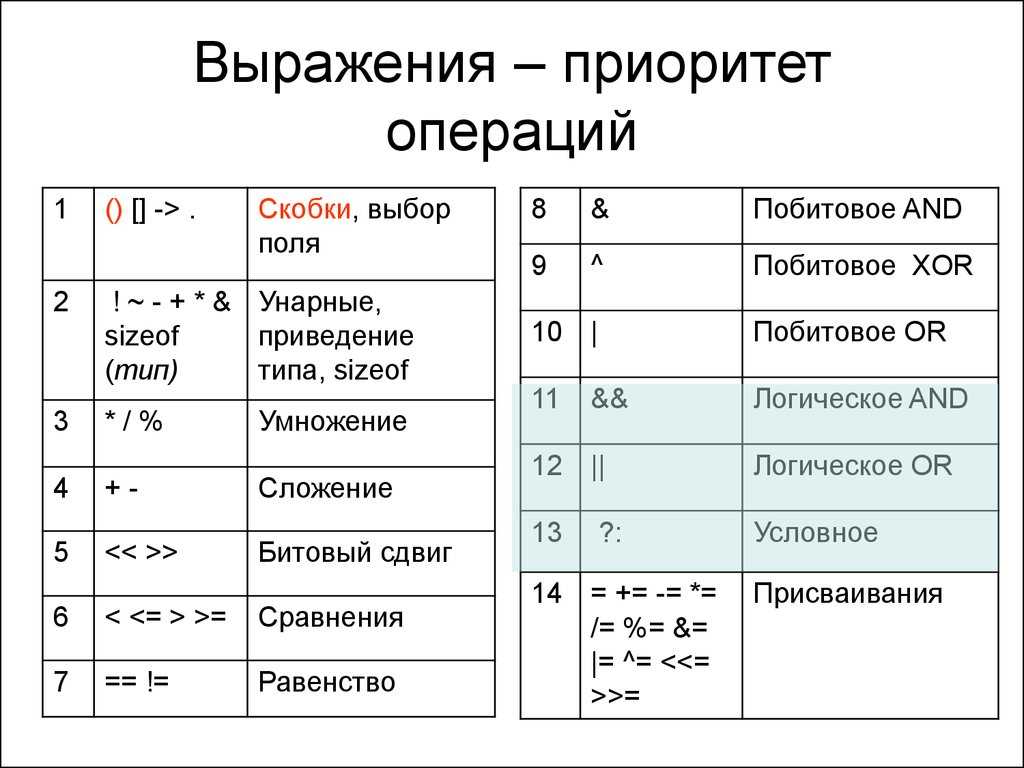
Порядок приоритетности (от наивысшего до самого низкого) в побитовых операторах при программировании на C:
Данные операнды используются в большинстве языков программирования. Например, при написании кода в Javascript побитовые операции будет теми же, что и вышеперечисленные. Это вызвано базовыми математическими основами, на которых базируется программный код. В частности, побитовые операции в Java, в свою очередь, полностью тождественны Javascript.
Бит и программирование на C и других языках
Бит является наименьшей единицей измерения, используемой для количественной оценки компьютерных данных. Он содержит одно двоичное значение — 0 или 1.
Хотя один бит может определять логическое значение True (1) или False (0), как отдельная единица он используется редко. Поэтому в компьютерном хранилище биты часто группируются в 8-битные кластеры, называемые байтами. Поскольку байт содержит восемь бит, каждый из которых имеет два возможных значения, в побитовых операциях в Си (язык программирования) один байт может иметь 28 или 256 различных значений.
Поскольку байт содержит восемь бит, каждый из которых имеет два возможных значения, в побитовых операциях в Си (язык программирования) один байт может иметь 28 или 256 различных значений.
Термины «биты» и «байты» часто путаются и даже используются взаимозаменяемо, поскольку звучат одинаково и оба сокращаются буквой «Б». Однако при правильном написании биты сокращаются в нижнем регистре «b», а байты сокращаются в верхнем регистре — «B». Важно не путать эти два термина, так как любое измерение в байтах содержит в восемь раз больше бит. Например, небольшой текстовый файл размером 4 КБ содержит 4000 байт или 32 000 бит.Как правило, файлы, устройства хранения и емкость хранилища измеряются в байтах, а скорости передачи данных измеряются в битах. Например, карта памяти SSD может иметь емкость 240 ГБ, тогда как загрузка может переноситься со скоростью 10 Мбит/с. Кроме того, биты также используются для описания архитектуры процессора, такой как 32-разрядный или 64-разрядный процессор.

Побитовые операции в паскале
Побитовый уровень операций в паскале включает в себя работу с отдельными битами, которые являются наименьшими единицами данных на компьютере. Хотя компьютеры способны манипулировать битами, они обычно хранят данные и выполняют инструкции в битовых кратных значениях, называемых байтами. Большинство языков программирования, в том числе побитовые операции в Delphi, управляют группами из 8, 16 или 32 бит.
Описание процесса
Поразрядный оператор — это символ, представляющий действие, которое работает с данными на уровне бит, а не с байтами или большими единицами данных, как это чаще встречается.
Большинство обычных операторов работают с одним или несколькими байтами, которые в большинстве систем содержат восемь бит. Поскольку они обеспечивают большую точность и требуют меньшего количества ресурсов, побитовые операторы могут сделать код более быстрым и эффективным. Примеры использования побитовых операций включают в себя:
шифрование;
сжатие;
графику;
связь по портам/сокетам;
программирование встроенных систем;
машины с конечным состоянием.

Побитовый оператор работает с двоичным представлением числа, а не с его значением. Операнд рассматривается как набор бит, а не как один номер. Побитовые операторы аналогичны в большинстве поддерживающих их языков — C, Java, JavaScript, Python и Visual Basic.
Почему это важно использовать
Побитовые операции абсолютно необходимы при программировании аппаратных регистров во встроенных системах. Каждый процессор имеет один или несколько регистров (обычно определенный адрес памяти), которые контролируют, включено ли прерывание или отключено. Чтобы позволить прерыванию запускать обычный процесс, необходимо установить бит разрешения для этого типа прерывания, а главное, не изменять ни один из остальных битов в регистре.Когда прерывание срабатывает, оно обычно устанавливает бит в регистре состояния, так что одна служебная процедура может определять точную причину прерывания. Тестирование отдельных битов позволяет быстро декодировать источник прерываний.
Во многих встроенных системах общая доступная оперативная память может быть 64, 128 или 256 байт. В этой среде обычно используется один байт для хранения нескольких элементов данных и булевых флагов, а затем используются битовые операции для установки и чтения их.
В этой среде обычно используется один байт для хранения нескольких элементов данных и булевых флагов, а затем используются битовые операции для установки и чтения их.Обработка битов в Java — операции побитового сдвига и битового сдвига
Java позволяет вам манипулировать целыми числами на уровне битов, что означает работу с определенными битами, которые представляют целое число. В некоторых случаях это может быть очень удобно.
Побитовые операторы
Вы, несомненно, знакомы с арифметическими операторами, такими как + — * / или %. Вы также наверняка знаете такие логические операторы, как & или |. Оказывается, есть еще один, немного менее известный набор операторов, которые манипулируют числами на уровне битов. Внутри каждое число хранится в двоичном формате — то есть 0 и 1.
Эти операторы могут выполняться над целочисленными типами и их вариантами, то есть
- байт (8 бит)
- короткий (16 бит)
- целое число (32 бита)
- длинный (64 бит)
- и даже символ (16 бит)
Унарный оператор побитового дополнения [~]
Это причудливое название в основном означает битовое отрицание.
 Он берет каждый бит числа и переворачивает его значение. То есть — 0 становится 1 и наоборот. Унарный означает, что ему нужен только один операнд. Оператор – это ~, и он ставится перед числом: 9.0003
Он берет каждый бит числа и переворачивает его значение. То есть — 0 становится 1 и наоборот. Унарный означает, что ему нужен только один операнд. Оператор – это ~, и он ставится перед числом: 9.0003~someVariable
или
Например, давайте использовать ~42:
- Двоичное представление числа 42 равно 101010.
- Поскольку 42 — это целое число, оно представляется как 32-битное значение, то есть 32 единицы или нули.
- Таким образом, все позиции слева от 101010 на самом деле заполнены нулями до 32 бит.
- То есть 00000000 00000000 00000000 00101010
- Перевернутое значение числа, указанного выше, тогда будет 11111111 11111111 11111111 11010101
Побитовое И [&]
В отличие от оператора побитового дополнения, другим побитовым операторам требуется два операнда.
A & B означает, что все биты обоих чисел сравниваются один за другим, и результирующее число вычисляется на основе значений битов из чисел A и B.
 Побитовое И похоже на логическое И в том смысле, что оно приводит к 1 только тогда, когда два сравниваемых бита равны 1. В противном случае это дает 0.
Побитовое И похоже на логическое И в том смысле, что оно приводит к 1 только тогда, когда два сравниваемых бита равны 1. В противном случае это дает 0.Например: 1010 и 1100 дадут 1000, поскольку первый бит слева является единственным, где оба операнда содержат 1. 9Б
1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 0 0 Операторы сдвига битов
Сдвиг влево со знаком [
<<]Сдвиг влево со знаком принимает два операнда. Он берет битовую комбинацию первого операнда и сдвигает ее влево на количество разрядов, заданное вторым операндом. Например 5 << 3: Что происходит в этом случае - каждый бит в двоичном представлении целого числа 5 сдвигается на 3 позиции влево.
 Все места слева заполнены нулями. То есть: 9 н .
Все места слева заполнены нулями. То есть: 9 н .Есть несколько дополнительных интересных аспектов:
- Несмотря на то, что вы можете использовать сдвиг byte, short или char, они преобразуются в 32-битное целое перед сдвигом
- Операторы битового сдвига никогда не выдают исключение
- Правый операнд (количество позиций для сдвига) уменьшается по модулю 32. То есть 5 <<35 эквивалентно 5 << 3.
Отрицательные целые числа в Java
На самом деле существует два типа сдвига вправо. Подписанные и неподписанные. Разница в том, как они обрабатывают отрицательные числа. Чтобы понять разницу, необходимо знать, как отрицательные числа представлены в Java. Двоичное представление само по себе не дает информации о том, является ли число отрицательным. Должно быть специальное правило, чтобы определить, как представлять отрицательные числа в двоичном формате. Существует несколько подходов к этой проблеме.
Одно из решений состоит в том, что самый левый (самый значащий) бит является битом знака.
 Это означает, что его значение указывает, является ли число положительным или отрицательным. Однако у этого есть некоторые недостатки, такие как наличие двух способов представления нуля.
Это означает, что его значение указывает, является ли число положительным или отрицательным. Однако у этого есть некоторые недостатки, такие как наличие двух способов представления нуля.Java использует другой подход, который называется дополнением до двух . Отрицательные числа представляются путем инвертирования (переворачивания) всех битов с последующим добавлением 1. Тем не менее, если крайний левый бит равен 0, число положительное. В противном случае оно отрицательное. 9 n -1 в случае нечетных чисел.
Сдвиг вправо без знака [>>>]
В отличие от сдвига со знаком, беззнаковый сдвиг не учитывает знаковые биты, он просто сдвигает все биты вправо и дополняет результат нулями слева. Это означает, что для отрицательных чисел результат всегда положительный. Знаковые и беззнаковые сдвиги вправо имеют одинаковый результат для положительных чисел.
Составные операторы присваивания
Java предлагает более короткий синтаксис для присваивания результатов арифметических или побитовых операций.
 Поэтому вместо того, чтобы писать это:
Поэтому вместо того, чтобы писать это:х = х + 1;
Вы можете использовать более короткую версию, которая будет обрабатывать как сложение, так и присваивание с помощью всего одного оператора:
x += 1;
Вы, вероятно, знакомы с составными операторами присваивания для арифметических операций, таких как
+=,-=или*=. Но в дополнение к этому Java также предлагает варианты побитовых операторов:Оператор Пример Эквивалентно 95&= х &= 5 х = х и 5 <<= х <<= 5 х = х << 5 >>= х >>= 5 х = х >> 5 >>>= х >>>= 5 х = х >>> 5 Обратите внимание, что для унарного оператора побитового дополнения [~] не существует составного оператора присваивания.

Заключение
Манипуляции с битами могут быть очень удобными в некоторых случаях и действительно эффективными. Однако за повышение производительности приходится платить. Удобочитаемость сильно страдает, это может вызвать недоумение у тех, кто не знаком с концепцией манипулирования битами. Если сценарий, который вы используете, не критичен к производительности, вы можете подумать, действительно ли компромисс между производительностью и удобочитаемостью того стоит, и, возможно, переписать свое решение, сделав его более удобочитаемым. Не используйте манипуляции с битами везде, где только возможно, только потому, что вы узнали новую интересную концепцию.
Как использовать операторы обработки битов Java
Поиск
Программистам иногда приходится опускаться до уровня битов и байтов при работе с низкоуровневыми данными. Это особенно заметно при разработке программного обеспечения для тестового оборудования, сетей, операционных систем или при установлении прямой связи с оборудованием.
 В любом случае, Java предоставляет возможности для обширных манипуляций с битами, и каждый может использовать их в соответствии со своими потребностями. В этой статье представлена справочная информация, связанная с этой возможностью и использованием побитовых операторов, доступных в Java.
В любом случае, Java предоставляет возможности для обширных манипуляций с битами, и каждый может использовать их в соответствии со своими потребностями. В этой статье представлена справочная информация, связанная с этой возможностью и использованием побитовых операторов, доступных в Java.Биты и байты
Бит происходит от фразы «двоичная цифра», представленной 0 или 1. Комбинация этих двух, казалось бы, простых чисел может нести много информации. 0 в основном означает off/false и 1 означает on/true . Проще говоря, переключатель может сигнализировать об одном из двух: либо выключено (0), либо включено (1). Теперь использование двух переключателей поочередно/вместе дает 2 2 = 4 таких сигнала — 00, 01, 10, 11. Три переключателя дадут 2 3 = 8 сигналов — 000, 001, 010, 011, 100, 101, 110, 111. Четыре переключателя, 16 сигналов и так далее. Отдельные биты, объединенные в группу из восьми, называются байт (8 бит = 1 байт).
 Количество сигналов, обеспечиваемых 8-битной или 1-байтовой обработкой, равно 2 8 = 256. По мере увеличения количества байтов единицей измерения становится килобайт (2 10 ), мегабайт (2 20 ), гигабайт (2 30 ) и так далее.
Количество сигналов, обеспечиваемых 8-битной или 1-байтовой обработкой, равно 2 8 = 256. По мере увеличения количества байтов единицей измерения становится килобайт (2 10 ), мегабайт (2 20 ), гигабайт (2 30 ) и так далее.Компьютеры внутренне представляют все данные в виде последовательности битов. Точнее, это даже не биты, а электрические заряды, представленные как имеющие определенные напряжения, равные 1/on/true , а его отсутствие или недостаток как 0/off/false . Эта простая идея дает значительный толчок для формулирования сигнальной схемы в математическом выражении и решает ее, как и любую математическую задачу. Именно из-за этого удобства сигналы отображаются в двоичные числа. Существует раздел математики, специально занимающийся бинарной логикой, называемый Булевой алгеброй , названный в честь английского математика и логика Джорджа Буля. Булева алгебра предоставляет принципы двоичной арифметики, которые можно прекрасно использовать в качестве инструмента для создания логических схем.

Когда мы говорим двоичная арифметика , основными операторами, используемыми с бинарными операциями, являются И, ИЛИ и НЕ. Кроме того, существуют другие производные операторы, такие как И-НЕ (НЕ И), ИЛИ (НЕ ИЛИ), Исключающее ИЛИ/ИСКЛЮЧАЮЩЕЕ ИЛИ (Исключающее ИЛИ) и Исключающее ИЛИ/ИСКЛЮЧАЮЩЕЕ ИЛИ (Исключающее ИЛИ). Таблица истинности с основными операторами показана на рисунке 1:
Рисунок 1: Таблица истинности
Другие производные операторы — НЕ-И, ИЛИ-НЕ и Экс-НЕ — не что иное, как оператор НЕ, добавленный к результату этих основных операторов.
Типы данных
В Java существует тип данных, называемый байт , для хранения восьмибитной последовательности. Если требуется хранить информацию более восьми бит, существует много других типов данных, но побитовые операторы работают только с целочисленными операндами, такими как byte, char, short, int и long .
 В указанном порядке каждая из них может хранить больше битовых последовательностей, чем предыдущая. Побитовые операторы не работают с операндами с плавающей запятой. 9), сдвиг влево (<<), сдвиг вправо со знаком (>>), сдвиг вправо без знака (>>>) и побитовое дополнение (~). Они работают так, как указано выше, с помощью таблиц истинности. Операторы сдвига влево и вправо будут объяснены далее в статье.
В указанном порядке каждая из них может хранить больше битовых последовательностей, чем предыдущая. Побитовые операторы не работают с операндами с плавающей запятой. 9), сдвиг влево (<<), сдвиг вправо со знаком (>>), сдвиг вправо без знака (>>>) и побитовое дополнение (~). Они работают так, как указано выше, с помощью таблиц истинности. Операторы сдвига влево и вправо будут объяснены далее в статье.Побитовый оператор и логический оператор
Стоит отметить, что операторы короткого замыкания, такие как логическое И (&&) и логическое ИЛИ (||), не следует путать с побитовым И (&) и побитовое ИЛИ (|), потому что они имеют разное значение. Логические операторы могут быть обозначены как ленивых вычислений , тогда как побитовые операторы стремятся к жадным вычислениям операторов. Это означает, что побитовые операторы И (&) и ИЛИ (|) оценивают обе стороны операции. С другой стороны, логические операторы И (&&) и ИЛИ (||) оценивают левую часть операции; если это true , они оценивают только правую сторону.

Смущает то, что в большинстве случаев они приводят к одному и тому же выводу. Вот пример, иллюстрирующий это.
пакет org.mano.example; открытый класс BitwiseOperatorDemo { public static void main( String [] args ) { Система. из .println ((false | ложь) ? "истина" : "ложь" ) ; Система. из .println ((false | верно) ? "правда" : "ложь" ) ; Система. из .println ((true | ложь) ? "истина" : "ложь" ) ; Система. из .println ((true | верно) ? "истина" : "ложь" ) ; Система. из .println ((false ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false ||
верно) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
верно) ? "истина" : "ложь" ) ;
Система. из .println (
"---------------------------------------------------------------------" ) ;
Система. из .println ((ложь и ложь)
? "истина" : "ложь" ) ;
Система.
из .println ((false ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false ||
верно) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
верно) ? "истина" : "ложь" ) ;
Система. из .println (
"---------------------------------------------------------------------" ) ;
Система. из .println ((ложь и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((ложь и правда)
? "истина" : "ложь" ) ;
Система. из .println ((истина и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((истина и истина)
? "истина" : "ложь" ) ;
Система. из .println ((false &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false &&
верно) ? "истина" : "ложь" ) ;
Система. вне .println ((правда &&
ложь) ? "истина" : "ложь" ) ;
Система.
из .println ((ложь и правда)
? "истина" : "ложь" ) ;
Система. из .println ((истина и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((истина и истина)
? "истина" : "ложь" ) ;
Система. из .println ((false &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false &&
верно) ? "истина" : "ложь" ) ;
Система. вне .println ((правда &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда &&
верно) ? "истина" : "ложь" ) ;
}
из .println ((правда &&
верно) ? "истина" : "ложь" ) ;
}
Выход
Ложь истинный истинный истинный ЛОЖЬ истинный истинный истинный ----------------------------------------- ЛОЖЬ ЛОЖЬ ЛОЖЬ истинный ЛОЖЬ ЛОЖЬ ЛОЖЬ истинный
Обратите внимание на следующий пример; это проясняет суть различия. Операции логического И и логического ИЛИ даже не вызывают функцию f2(), если только возвращаемое значение метода f1() не является истинным. Но это не относится к операторам побитового И и побитового ИЛИ. Обе стороны операции оцениваются в любом случае.
пакет org.mano.example; открытый класс BitwiseOperatorDemo { public static void main( Строка [] аргументы ) { если ( f1 () | f2 ()) Система. out .println ( "побитовое ИЛИ" ) ;
если ( ! f1 () и f2 ())
Система. out .println ( "побитовое И" ) ;
Система. вне .println (
"------------------------------------------------" ) ;
если ( f1 () || f2 ())
Система. из .println ( "логическое ИЛИ" ) ;
если ( ! f1 () && f2 ())
Система. из .println ( "логическое-И" ) ;
}
публичное статическое логическое значение f1() {
Система.
out .println ( "побитовое ИЛИ" ) ;
если ( ! f1 () и f2 ())
Система. out .println ( "побитовое И" ) ;
Система. вне .println (
"------------------------------------------------" ) ;
если ( f1 () || f2 ())
Система. из .println ( "логическое ИЛИ" ) ;
если ( ! f1 () && f2 ())
Система. из .println ( "логическое-И" ) ;
}
публичное статическое логическое значение f1() {
Система. out .println ( "Вызвана функция f1" ) ;
вернуть истину ;
}
публичное статическое логическое значение f2() {
Система. out .println ( "Вызвана функция f2" ) ;
вернуть истину ;
}
} 9) операторы сравнивают два операнда побитно.
out .println ( "Вызвана функция f1" ) ;
вернуть истину ;
}
публичное статическое логическое значение f2() {
Система. out .println ( "Вызвана функция f2" ) ;
вернуть истину ;
}
} 9) операторы сравнивают два операнда побитно. - Оператор И (&) устанавливает бит результата в 1, только если оба бита операнда равны 1.
- Оператор ИЛИ (|), с другой стороны, устанавливает бит результата в 1, когда один или оба бита операнда равны 1.
- Оператор Ex-OR устанавливает бит результата в 1, если соответствующий бит ровно одного из его операндов равен 1.
- Оператор сдвига влево (<<) сдвигает биты своего левого операнда влево в соответствии с числом, указанным в правом операнде. Нули вставляются справа.

- Оператор сдвига вправо со знаком (>>) сдвигает бит своего левого операнда вправо в соответствии с количеством битов, указанным правым операндом. Поскольку оператор сохраняет знаковый бит операнда, отрицательный операнд вставляет 1t слева; в противном случае вводятся 0. Этот метод поддерживает знаковый бит операнда.
- Оператор беззнакового сдвига вправо (>>>) аналогичен оператору сдвига влево, за исключением того, что работает в обратном направлении. Это означает, что оператор сдвигает биты в своем левом операнде вправо на количество битов, указанное правым операндом. Нули вставляются слева.
- Оператор побитового дополнения (~) устанавливает все нулевые биты в своем операнде в 1 и все 1 в 0.
Краткий пример
package org.mano.example; открытый класс BitwiseOperatorDemo { public static void main( String [] args ) { интервал а = -10; интервал б = -6; Система. из .print ( а + ":" ) ;
showBits ( a ) ;
Система. из .print ( b + ":" ) ;
showBits ( б ) ;
Система. из .print ( "И (a & b): " ) ;
showBits ( a & b ) ;
Система. из .print 9б ) ;
Система. из .print ( "сдвиг влево (a << 2): " ) ;
showBits ( a << 2 ) ;
Система. из .print ( "со знаком правый сдвиг
(а >> 2): ") ;
showBits ( a >> 2 ) ;
Система.
из .print ( а + ":" ) ;
showBits ( a ) ;
Система. из .print ( b + ":" ) ;
showBits ( б ) ;
Система. из .print ( "И (a & b): " ) ;
showBits ( a & b ) ;
Система. из .print 9б ) ;
Система. из .print ( "сдвиг влево (a << 2): " ) ;
showBits ( a << 2 ) ;
Система. из .print ( "со знаком правый сдвиг
(а >> 2): ") ;
showBits ( a >> 2 ) ;
Система. аут .print ( "правый сдвиг
(а >>> 2): ") ;
showBits ( a >>> 2 ) ;
Система. из .print ( "Дополнение (~a): " ) ;
showBits ( ~a ) ;
}
public static void showBits (int param ) {
int маска = 1 << 31;
для (целое i = 1; i <= 32; i++,
параметр <<= 1 ) {
Система. из .print (( параметр и маска ) ==
0 ? «0»: «1» ) ;
если ( я % 8 == 0 )
Система. из .print ( " " ) ;
}
Система.
аут .print ( "правый сдвиг
(а >>> 2): ") ;
showBits ( a >>> 2 ) ;
Система. из .print ( "Дополнение (~a): " ) ;
showBits ( ~a ) ;
}
public static void showBits (int param ) {
int маска = 1 << 31;
для (целое i = 1; i <= 32; i++,
параметр <<= 1 ) {
Система. из .print (( параметр и маска ) ==
0 ? «0»: «1» ) ;
если ( я % 8 == 0 )
Система. из .print ( " " ) ;
}
Система. из .println () ;
}
}
из .println () ;
}
}
Выход 9б): 00000000 00000000 00000000 00001100 сдвиг влево (a << 2): 11111111 11111111 11111111 11011000 сдвиг вправо со знаком (a >> 2): 11111111 11111111 11111111 11111101 сдвиг вправо (a >>> 2): 00111111 11111111 11111111 11111101 Дополнение (~а): 00000000 00000000 00000000 00001001
Класс BitSet
Java предоставляет специальный класс BitSet в пакете java.util для работы с битами. Этот класс можно использовать для более удобного выполнения операций над битами. Обратитесь к статье «Изучение Java BitSet» для получения более подробной информации о его использовании.
Заключение
Битовую операцию можно использовать так же, как и любой другой оператор в Java. Единственная разница между ним и другими операциями заключается в том, что он вычисляет побитовое значение. Иногда побитовую операцию можно комбинировать с другими бинарными операторами.
 Однако обратите внимание, что побитовые операторы работают только с целочисленными типами: byte, char, short, int и long . Типы с плавающей запятой, такие как float и double , нельзя использовать с побитовыми операторами.
Однако обратите внимание, что побитовые операторы работают только с целочисленными типами: byte, char, short, int и long . Типы с плавающей запятой, такие как float и double , нельзя использовать с побитовыми операторами.Похожие статьи
вариантов использования побитовых операторов в реальной жизни | Sreedev
Как разработчик вы наверняка когда-нибудь узнали о побитовых операторах и подумали про себя. «Ха, это опрятно. но где бы я на самом деле использовать его?». Это то, что мы сегодня рассмотрим.
Современный мир вычислений и разработки программного обеспечения убрал все сложности до такой степени, что вам действительно не нужно знать, как выполняется код, который вы пишете.
Хотя это подходит для большинства случаев, когда ваш код выполняется на серверах и мощных компьютерах, вы столкнетесь с серьезными проблемами при работе на устройствах с ограниченными ресурсами, таких как микроконтроллеры и ПЛИС.
Плата для разработки ESP32 Вам нужно будет знать, как ваш код выполняется на этих устройствах, чтобы оптимизировать его для работы на ограниченных ресурсах. (Килобайты оперативной памяти и кГц тактовой частоты).
Вам нужно будет знать, как ваш код выполняется на этих устройствах, чтобы оптимизировать его для работы на ограниченных ресурсах. (Килобайты оперативной памяти и кГц тактовой частоты).Понимание побитовых операторов сделает вас на шаг ближе к оптимизации. Давайте сначала разберемся, что такое побитовые операторы. Обратите внимание, что в этой статье рассматривается использование побитовых операторов в C, но логика и синтаксис остаются общими для большинства языков. Также ожидается, что вы знаете и понимаете преобразование двоичного кода в десятичный и десятичного в двоичный. Если вы этого еще не знаете, в Интернете есть множество ресурсов, которые помогут вам научиться этому.
- Что такое побитовые операторы?
- Различные побитовые операторы и их функции
- Практическое использование побитовых операторов
(Если вы уже знаете побитовые операторы, вы можете сразу перейти к этому разделу) уровень.Что я имею в виду? Они помогают вам манипулировать битами, составляющими фрагмент данных, представленный типом данных.
Побитовые операторы, их приоритет и ассоциативность Это станет более понятным, когда мы углубимся в тему. Давайте теперь посмотрим, какие различные побитовые операторы нам доступны.
Это станет более понятным, когда мы углубимся в тему. Давайте теперь посмотрим, какие различные побитовые операторы нам доступны.Используя оператор sizeof(), мы можем найти количество байтов, которое представляет каждый тип данных, и, поскольку каждый байт состоит из 8 бит, мы можем узнать общее количество битов, занимаемых каждым типом данных. тип данных с некоторой магией умножения.
Давайте теперь подробно рассмотрим каждого оператора.
& Побитовое И
Оператор побитового И (&) берет два операнда и сравнивает операнды побитно и устанавливает соответствующий выходной бит в 1 тогда и только тогда, когда оба входных бита равны 1. Вот таблица истинности для побитового И оператор:
Давайте возьмем следующий код, например
, поэтому значение переменной x равно 5, а значение переменной y равно 6. Компьютер, на котором я работаю, является 64-битной машиной, поэтому sizeof(int) равен 4 bytes so the binary representation of 5 world be:
00000000 00000000 00000000 00000101and the binary representation of 6 would be:
00000000 00000000 00000000 00000110For the sake of simplicity, let’s just take the last byte во внимание и выполним над ними операцию побитового И.

Как видите, биты 5 и 6 сравнивались, и в результате выходной байт был установлен на 00000100 , что является двоичным представлением числа 4. Вот как мы пришли к «5 и 6 = 4”.
| Побитовое ИЛИ
Оператор побитового ИЛИ принимает два операнда так же, как побитовое И, и сравнивает их побитно, но вместо установки выходного бита в 1 только тогда, когда оба входных бита равны 1, он следует следующей таблице истинности:
Давайте посмотрим в приведенном ниже примере: 96 = 3
Как вы спрашиваете? давайте посмотрим на биты
Сравнение входных битов в соответствии с таблицей истинности побитового исключающего ИЛИ. Мы приходим к 00000011 , что является двоичным представлением 3.
~ Побитовое НЕ
Побитовый оператор НЕ немного отличается от других операторов, так как он принимает только один операнд. Побитовый оператор НЕ инвертирует биты своего операнда. Давайте посмотрим на следующий пример, чтобы лучше понять его:
Приведенная выше программа выдаст «~5=-6» в качестве вывода.
 Давайте посмотрим, как программа пришла к значению -6, когда побитовый оператор НЕ был применен к 5.
Давайте посмотрим, как программа пришла к значению -6, когда побитовый оператор НЕ был применен к 5.Поскольку отрицательные числа хранятся в виде дополнения до 2, «11111010» будет равно -6 в десятичном представлении.
<< Оператор побитового сдвига влевоОператор сдвига влево, как следует из названия, перемещает биты в своем левом операнде вправо на количество позиций, указанное в правом операнде.
Таким образом, если двоичное представление числа 5 равно 00000101, то применение оператора сдвига, например, «5 << 2», сдвинет биты влево на две позиции, удалив 2 старших значащих бита и добавив 2 нуля в качестве младших значащих битов. . Двоичное представление результата будет 00010100, что равно 20 в десятичном представлении. Давайте посмотрим на это в коде.
Пока установленные вами биты не переполняются и не сбрасываются, каждый сдвиг влево на 1 позицию приводит к умножению левого операнда на 2.
Как и ожидалось, программа выводит результат «5 << 2 = 20”.

>> Оператор побитового сдвига вправо
Оператор побитового сдвига вправо очень похож на оператор сдвига влево. Верьте или нет, вместо того, чтобы сдвигать биты влево, он сдвигает биты вправо. Да, вы не видели, что тот приближается, не так ли?
По мере сдвига битов вправо младшие значащие биты отбрасываются, а в качестве старших значащих битов добавляется эквивалентное количество нулей.
Вот код.
Достаточно просто, когда мы сдвигаем биты 5 (00000101) на 2 позиции вправо, мы получаем (00000001), что в основном равно 1 в десятичном и двоичном формате, поэтому приведенный выше код напечатает «5 >> 2 = 1». .
До тех пор, пока установленные биты не переполняются и не теряются, каждый сдвиг вправо на 1 разряд приводит к делению левого операнда на 2.
Теперь, когда вы, наконец, освоили побитовые операторы, вы, вероятно, думаете: «Что мне делать с этим обилием информации?».
Я вас прикрою. В следующем разделе мы обсудим некоторые практические применения побитовых операторов.

1. Хранение нескольких логических флагов
При работе с устройствами с ограниченной памятью вы не можете позволить себе иметь тысячу логических флагов, назначенных переменным. Это действительно неэффективный способ хранения ваших флагов, потому что логические значения в C в основном имеют длину в байт. Нам не нужен целый байт, чтобы хранить только ноль или единицу. Остальные биты останутся нулевыми. Вы не можете позволить себе выбрасывать драгоценную память, когда работаете только с КБ ОЗУ.
Так какое решение? Давайте посмотрим на код.
Вы наверняка задавались вопросом, все это только для того, чтобы сэкономить 1 байт? ну это не совсем так. Увеличение потребления памяти на логический флаг составляет один байт, но при использовании побитовых флагов вам потребуется только дополнительный байт каждые 8 флагов, которые вы добавляете в программу. Чтобы увеличить или уменьшить количество флагов, вам просто нужно изменить тип данных. если вам нужно менее 8 флагов, вы можете использовать «unsigned char» .
 Если вам нужно более 8 флагов, вы можете использовать «unsigned long int» или «unsigned long long int» в зависимости от ваших требований.
Если вам нужно более 8 флагов, вы можете использовать «unsigned long int» или «unsigned long long int» в зависимости от ваших требований.2. Проверка четных и нечетных чисел
Еще один прием, которого можно достичь с помощью побитовых операторов, — это проверка, является ли целое число четным или нечетным. Давайте посмотрим, как мы можем это сделать.
Таким образом, логика !(x&1) заключается в том, что двоичное представление 1 равно 0001 (учитывая только 4 бита для простоты), а разрядное значение младшего значащего бита равно 1. Все нечетные числа могут быть представлены как 2n+1. Таким образом, младший бит всегда равен 1 для нечетных чисел. Таким образом, при сравнении любого нечетного числа с 0001 с помощью побитового И выходные байты будут 0001. Таким образом, используя логический оператор НЕ, мы можем проверять четные числа. Для нечетных чисел вам просто нужно удалить логическое НЕ и просто проверить (x & 1).
3. Замена переменных без использования третьей переменной
Таким образом, замена двух переменных без использования третьей переменной может быть достигнута без побитовых операторов, но поскольку вы уже знаете побитовые операторы, почему бы и нет?
4.
 Преобразование регистра текста (нижний и верхний регистр)
Преобразование регистра текста (нижний и верхний регистр)Итак, в приведенном выше примере мы используем побитовое И с символом «_» в качестве правильного операнда для преобразования каждого символа в строке в верхний регистр. А для преобразования в нижний регистр мы используем побитовый оператор ИЛИ с символом пробела ASCII в качестве правого операнда.
5. Проверка, является ли число степенью двойки
Чтобы понять, как работает приведенное выше условие, нам нужно понять свойство степеней двойки. Степени двойки, представленные в двоичном виде, имеют только один установленный бит, т. е. только один бит имеет значение 1. Любая степень двойки минус 1 будет иметь двоичное представление, в котором установлены все биты, кроме бита, представляющего следующее число (которое равно степень 2).
Используя побитовое И с числом n и n-1, мы можем заключить, что рассматриваемое число является степенью двойки, если оно возвращает 0.
Чтобы понять, как работает приведенное выше условие, нам нужно понять свойство степеней двойки.


 y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
}
y; //XOR x and y
while (z != 0) {
//увеличим счётчик, если последняя двоичная цифра = 1
bitCount += z & 1;
z = z >> 1; //сдвигаем z на единицу вправо
}
return bitCount;
} А чтобы получить из последовательности конкретное значение, нужна маска — двоичное число, которое «высвечивает» из массива нужный бит.
А чтобы получить из последовательности конкретное значение, нужна маска — двоичное число, которое «высвечивает» из массива нужный бит. Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности.
Хочу в IT!
Вы на практике попробуете разные направления: разработку на разных языках, аналитику данных, Data Science, менеджмент в IT. Это самый подходящий курс для построения карьеры в IT в новой реальности.
Хочу в IT!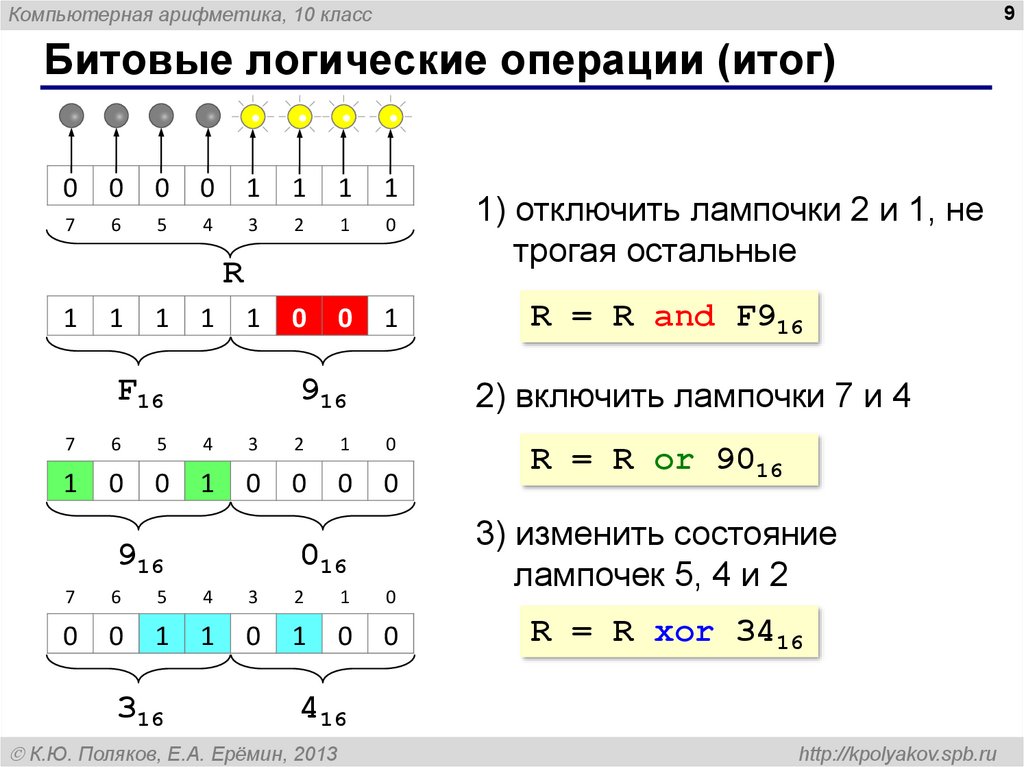
 Если на первый и второй вопросы ответы даны правильный, а на третий — неверно, получится список значений формата «правда, правда, ложь». Это булевы значения. В двоичном представлении их можно отобразить как 110, это число и есть битовая строка.
Если на первый и второй вопросы ответы даны правильный, а на третий — неверно, получится список значений формата «правда, правда, ложь». Это булевы значения. В двоичном представлении их можно отобразить как 110, это число и есть битовая строка. Работать с масками можно благодаря побитовым операциям — они попарно сравнивают конкретные биты двух чисел и применяют к ним логические операции. Первый бит одного числа сравнится с первым битом другого, второй — со вторым, и так далее. Это похоже на сложение и вычитание в столбик, когда человек работает с цифрами попарно. Только вместо сложения и вычитания — логические операции. Они возвращают 1 или 0 в зависимости от результатов сравнения.
Работать с масками можно благодаря побитовым операциям — они попарно сравнивают конкретные биты двух чисел и применяют к ним логические операции. Первый бит одного числа сравнится с первым битом другого, второй — со вторым, и так далее. Это похоже на сложение и вычитание в столбик, когда человек работает с цифрами попарно. Только вместо сложения и вычитания — логические операции. Они возвращают 1 или 0 в зависимости от результатов сравнения.
 При побитовой операции «1001 И 1000» результатом будет 1000 — это показывает, что нужный бит равен 1. А при операции «0001 И 1000» получится 0000 — это показывает, что бит равен 0.
При побитовой операции «1001 И 1000» результатом будет 1000 — это показывает, что нужный бит равен 1. А при операции «0001 И 1000» получится 0000 — это показывает, что бит равен 0. Вы можете узнать больше о побитовых операциях и о хранении информации в компьютере — для этого есть туториалы, интернет-статьи, учебники и профессиональные курсы.
Вы можете узнать больше о побитовых операциях и о хранении информации в компьютере — для этого есть туториалы, интернет-статьи, учебники и профессиональные курсы. Компьютеры работают в двоичном формате, что означает, что они хранят данные и выполняют вычисления, используя только нули и единицы.
Компьютеры работают в двоичном формате, что означает, что они хранят данные и выполняют вычисления, используя только нули и единицы.
 ) — результат является истиной, только если один из его операндов истинен. Он используется, в основном, для переключения определенных бит. Он также помогает заменять две переменные без использования третьей.
) — результат является истиной, только если один из его операндов истинен. Он используется, в основном, для переключения определенных бит. Он также помогает заменять две переменные без использования третьей.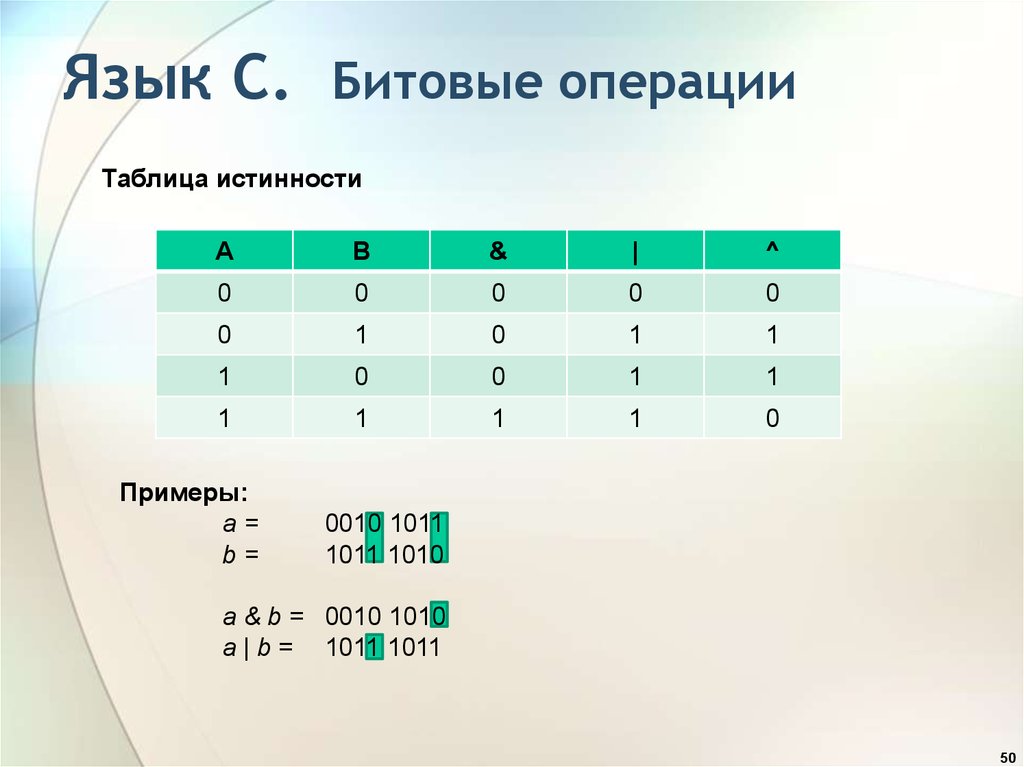 . Левый сдвиг (<<), правый сдвиг (>>) и правый сдвиг нулевой заливки (>>>>) иногда упоминаются как побитовые операторы и называются операторами сдвига бит.
. Левый сдвиг (<<), правый сдвиг (>>) и правый сдвиг нулевой заливки (>>>>) иногда упоминаются как побитовые операторы и называются операторами сдвига бит.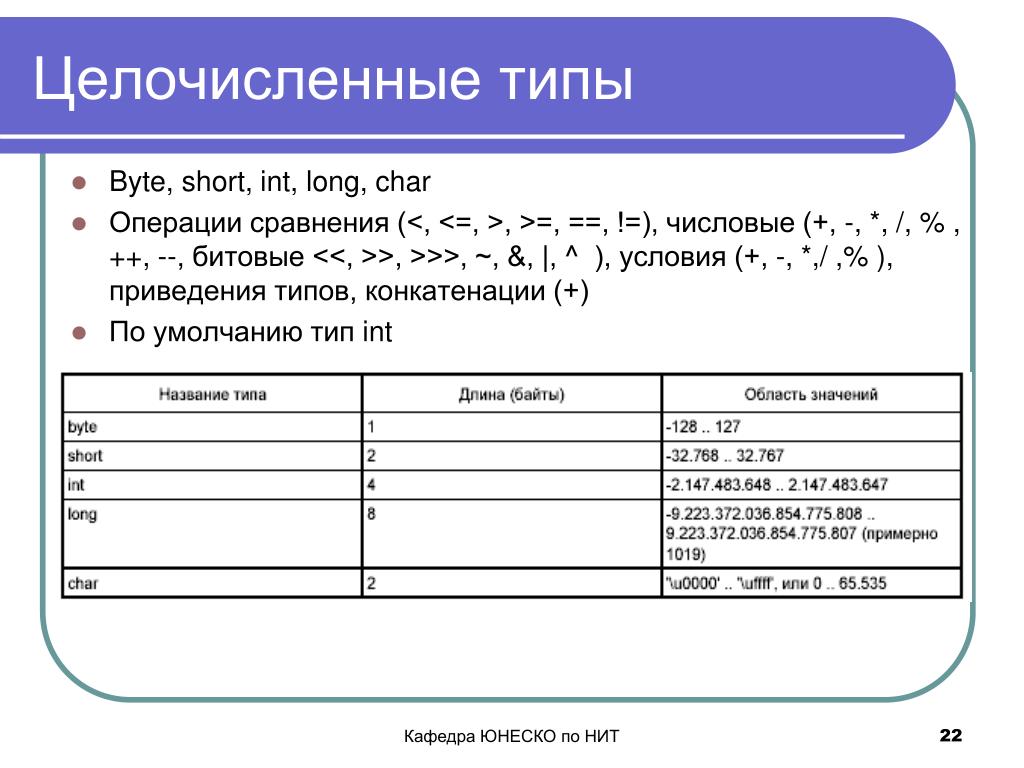 Поскольку байт содержит восемь бит, каждый из которых имеет два возможных значения, в побитовых операциях в Си (язык программирования) один байт может иметь 28 или 256 различных значений.
Поскольку байт содержит восемь бит, каждый из которых имеет два возможных значения, в побитовых операциях в Си (язык программирования) один байт может иметь 28 или 256 различных значений.

 В этой среде обычно используется один байт для хранения нескольких элементов данных и булевых флагов, а затем используются битовые операции для установки и чтения их.
В этой среде обычно используется один байт для хранения нескольких элементов данных и булевых флагов, а затем используются битовые операции для установки и чтения их. Он берет каждый бит числа и переворачивает его значение. То есть — 0 становится 1 и наоборот. Унарный означает, что ему нужен только один операнд. Оператор – это ~, и он ставится перед числом: 9.0003
Он берет каждый бит числа и переворачивает его значение. То есть — 0 становится 1 и наоборот. Унарный означает, что ему нужен только один операнд. Оператор – это ~, и он ставится перед числом: 9.0003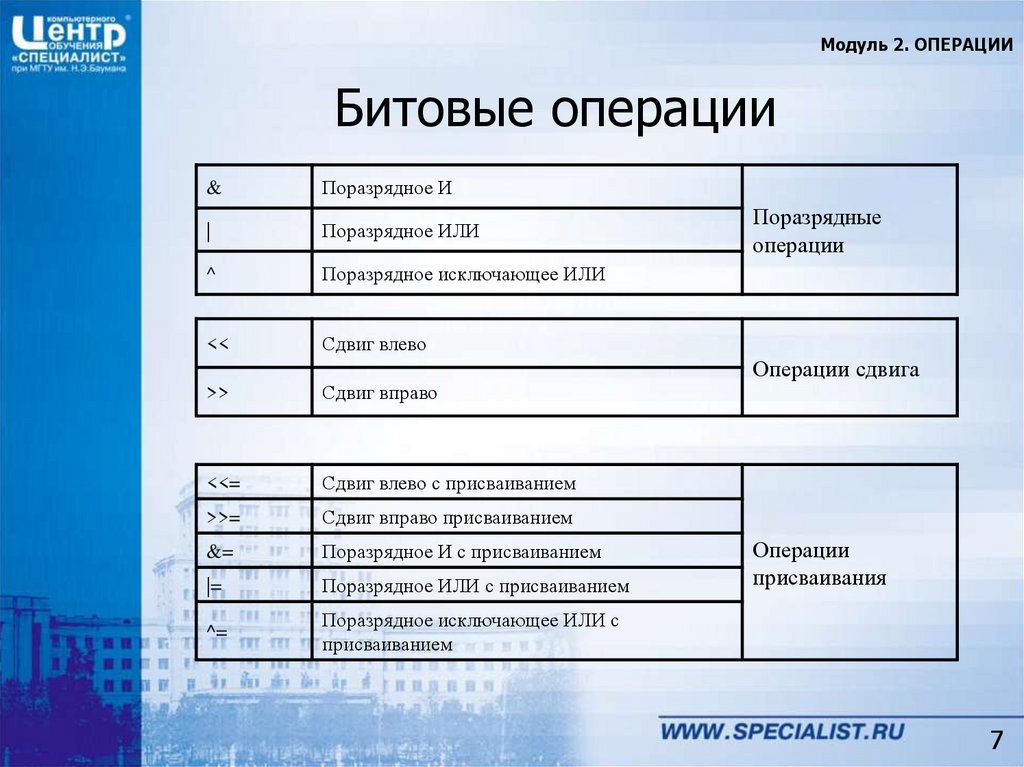 Побитовое И похоже на логическое И в том смысле, что оно приводит к 1 только тогда, когда два сравниваемых бита равны 1. В противном случае это дает 0.
Побитовое И похоже на логическое И в том смысле, что оно приводит к 1 только тогда, когда два сравниваемых бита равны 1. В противном случае это дает 0.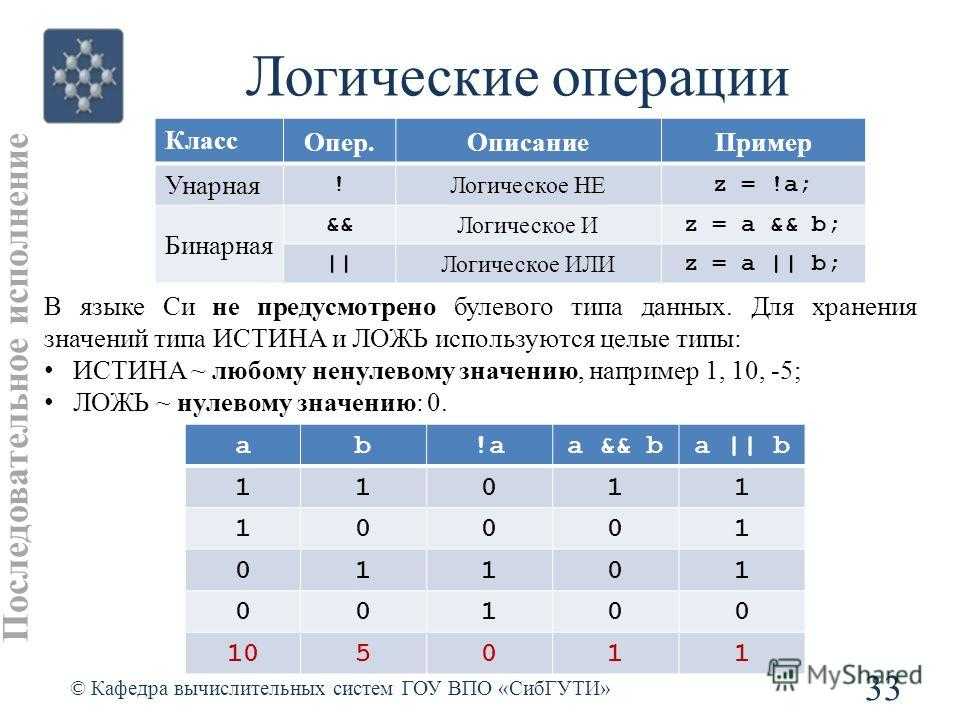 Все места слева заполнены нулями. То есть: 9 н .
Все места слева заполнены нулями. То есть: 9 н . Это означает, что его значение указывает, является ли число положительным или отрицательным. Однако у этого есть некоторые недостатки, такие как наличие двух способов представления нуля.
Это означает, что его значение указывает, является ли число положительным или отрицательным. Однако у этого есть некоторые недостатки, такие как наличие двух способов представления нуля. Поэтому вместо того, чтобы писать это:
Поэтому вместо того, чтобы писать это:
 В любом случае, Java предоставляет возможности для обширных манипуляций с битами, и каждый может использовать их в соответствии со своими потребностями. В этой статье представлена справочная информация, связанная с этой возможностью и использованием побитовых операторов, доступных в Java.
В любом случае, Java предоставляет возможности для обширных манипуляций с битами, и каждый может использовать их в соответствии со своими потребностями. В этой статье представлена справочная информация, связанная с этой возможностью и использованием побитовых операторов, доступных в Java. Количество сигналов, обеспечиваемых 8-битной или 1-байтовой обработкой, равно 2 8 = 256. По мере увеличения количества байтов единицей измерения становится килобайт (2 10 ), мегабайт (2 20 ), гигабайт (2 30 ) и так далее.
Количество сигналов, обеспечиваемых 8-битной или 1-байтовой обработкой, равно 2 8 = 256. По мере увеличения количества байтов единицей измерения становится килобайт (2 10 ), мегабайт (2 20 ), гигабайт (2 30 ) и так далее.
 В указанном порядке каждая из них может хранить больше битовых последовательностей, чем предыдущая. Побитовые операторы не работают с операндами с плавающей запятой. 9), сдвиг влево (<<), сдвиг вправо со знаком (>>), сдвиг вправо без знака (>>>) и побитовое дополнение (~). Они работают так, как указано выше, с помощью таблиц истинности. Операторы сдвига влево и вправо будут объяснены далее в статье.
В указанном порядке каждая из них может хранить больше битовых последовательностей, чем предыдущая. Побитовые операторы не работают с операндами с плавающей запятой. 9), сдвиг влево (<<), сдвиг вправо со знаком (>>), сдвиг вправо без знака (>>>) и побитовое дополнение (~). Они работают так, как указано выше, с помощью таблиц истинности. Операторы сдвига влево и вправо будут объяснены далее в статье.
 из .println ((false ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false ||
верно) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
верно) ? "истина" : "ложь" ) ;
Система. из .println (
"---------------------------------------------------------------------" ) ;
Система. из .println ((ложь и ложь)
? "истина" : "ложь" ) ;
Система.
из .println ((false ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false ||
верно) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда ||
верно) ? "истина" : "ложь" ) ;
Система. из .println (
"---------------------------------------------------------------------" ) ;
Система. из .println ((ложь и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((ложь и правда)
? "истина" : "ложь" ) ;
Система. из .println ((истина и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((истина и истина)
? "истина" : "ложь" ) ;
Система. из .println ((false &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false &&
верно) ? "истина" : "ложь" ) ;
Система. вне .println ((правда &&
ложь) ? "истина" : "ложь" ) ;
Система.
из .println ((ложь и правда)
? "истина" : "ложь" ) ;
Система. из .println ((истина и ложь)
? "истина" : "ложь" ) ;
Система. из .println ((истина и истина)
? "истина" : "ложь" ) ;
Система. из .println ((false &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((false &&
верно) ? "истина" : "ложь" ) ;
Система. вне .println ((правда &&
ложь) ? "истина" : "ложь" ) ;
Система. из .println ((правда &&
верно) ? "истина" : "ложь" ) ;
}
из .println ((правда &&
верно) ? "истина" : "ложь" ) ;
}
 out .println ( "побитовое ИЛИ" ) ;
если ( ! f1 () и f2 ())
Система. out .println ( "побитовое И" ) ;
Система. вне .println (
"------------------------------------------------" ) ;
если ( f1 () || f2 ())
Система. из .println ( "логическое ИЛИ" ) ;
если ( ! f1 () && f2 ())
Система. из .println ( "логическое-И" ) ;
}
публичное статическое логическое значение f1() {
Система.
out .println ( "побитовое ИЛИ" ) ;
если ( ! f1 () и f2 ())
Система. out .println ( "побитовое И" ) ;
Система. вне .println (
"------------------------------------------------" ) ;
если ( f1 () || f2 ())
Система. из .println ( "логическое ИЛИ" ) ;
если ( ! f1 () && f2 ())
Система. из .println ( "логическое-И" ) ;
}
публичное статическое логическое значение f1() {
Система. out .println ( "Вызвана функция f1" ) ;
вернуть истину ;
}
публичное статическое логическое значение f2() {
Система. out .println ( "Вызвана функция f2" ) ;
вернуть истину ;
}
} 9) операторы сравнивают два операнда побитно.
out .println ( "Вызвана функция f1" ) ;
вернуть истину ;
}
публичное статическое логическое значение f2() {
Система. out .println ( "Вызвана функция f2" ) ;
вернуть истину ;
}
} 9) операторы сравнивают два операнда побитно. 
 из .print ( а + ":" ) ;
showBits ( a ) ;
Система. из .print ( b + ":" ) ;
showBits ( б ) ;
Система. из .print ( "И (a & b): " ) ;
showBits ( a & b ) ;
Система. из .print 9б ) ;
Система. из .print ( "сдвиг влево (a << 2): " ) ;
showBits ( a << 2 ) ;
Система. из .print ( "со знаком правый сдвиг
(а >> 2): ") ;
showBits ( a >> 2 ) ;
Система.
из .print ( а + ":" ) ;
showBits ( a ) ;
Система. из .print ( b + ":" ) ;
showBits ( б ) ;
Система. из .print ( "И (a & b): " ) ;
showBits ( a & b ) ;
Система. из .print 9б ) ;
Система. из .print ( "сдвиг влево (a << 2): " ) ;
showBits ( a << 2 ) ;
Система. из .print ( "со знаком правый сдвиг
(а >> 2): ") ;
showBits ( a >> 2 ) ;
Система. аут .print ( "правый сдвиг
(а >>> 2): ") ;
showBits ( a >>> 2 ) ;
Система. из .print ( "Дополнение (~a): " ) ;
showBits ( ~a ) ;
}
public static void showBits (int param ) {
int маска = 1 << 31;
для (целое i = 1; i <= 32; i++,
параметр <<= 1 ) {
Система. из .print (( параметр и маска ) ==
0 ? «0»: «1» ) ;
если ( я % 8 == 0 )
Система. из .print ( " " ) ;
}
Система.
аут .print ( "правый сдвиг
(а >>> 2): ") ;
showBits ( a >>> 2 ) ;
Система. из .print ( "Дополнение (~a): " ) ;
showBits ( ~a ) ;
}
public static void showBits (int param ) {
int маска = 1 << 31;
для (целое i = 1; i <= 32; i++,
параметр <<= 1 ) {
Система. из .print (( параметр и маска ) ==
0 ? «0»: «1» ) ;
если ( я % 8 == 0 )
Система. из .print ( " " ) ;
}
Система. из .println () ;
}
}
из .println () ;
}
}
 Однако обратите внимание, что побитовые операторы работают только с целочисленными типами: byte, char, short, int и long . Типы с плавающей запятой, такие как float и double , нельзя использовать с побитовыми операторами.
Однако обратите внимание, что побитовые операторы работают только с целочисленными типами: byte, char, short, int и long . Типы с плавающей запятой, такие как float и double , нельзя использовать с побитовыми операторами.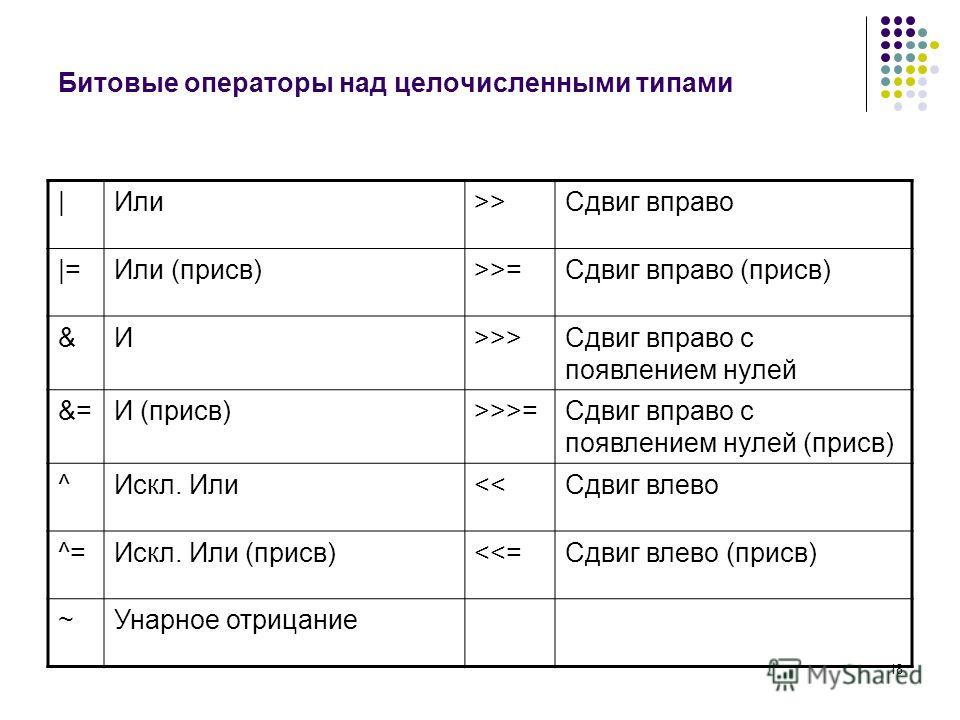 Вам нужно будет знать, как ваш код выполняется на этих устройствах, чтобы оптимизировать его для работы на ограниченных ресурсах. (Килобайты оперативной памяти и кГц тактовой частоты).
Вам нужно будет знать, как ваш код выполняется на этих устройствах, чтобы оптимизировать его для работы на ограниченных ресурсах. (Килобайты оперативной памяти и кГц тактовой частоты). Это станет более понятным, когда мы углубимся в тему. Давайте теперь посмотрим, какие различные побитовые операторы нам доступны.
Это станет более понятным, когда мы углубимся в тему. Давайте теперь посмотрим, какие различные побитовые операторы нам доступны.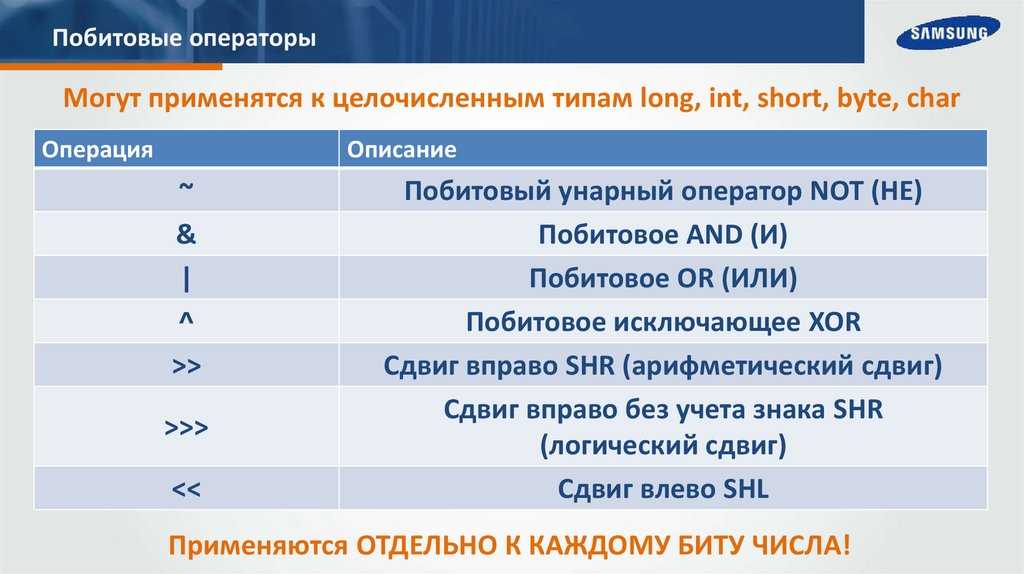
 Давайте посмотрим, как программа пришла к значению -6, когда побитовый оператор НЕ был применен к 5.
Давайте посмотрим, как программа пришла к значению -6, когда побитовый оператор НЕ был применен к 5.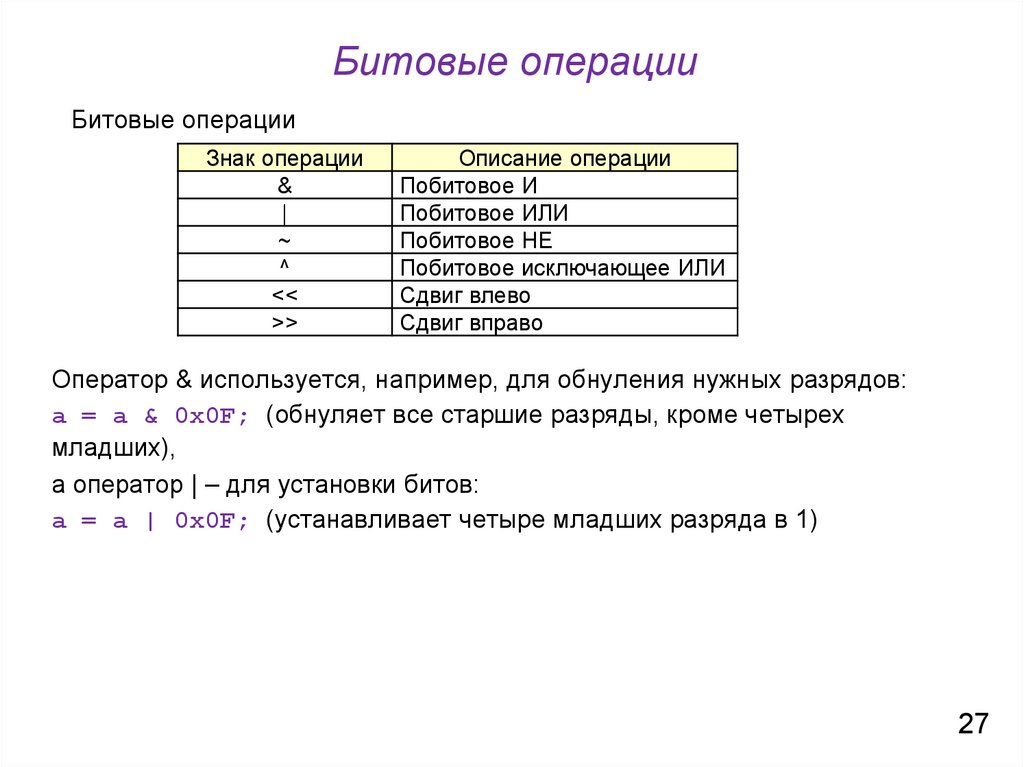

 Если вам нужно более 8 флагов, вы можете использовать «unsigned long int» или «unsigned long long int» в зависимости от ваших требований.
Если вам нужно более 8 флагов, вы можете использовать «unsigned long int» или «unsigned long long int» в зависимости от ваших требований. Преобразование регистра текста (нижний и верхний регистр)
Преобразование регистра текста (нижний и верхний регистр)