Проблемы точности чисел float в Python.
Числа с плавающей точкой представлены в компьютерах в виде двоичных дробей. Например, десятичная дробь 0.125 имеет значение 1/10 + 2/100 + 5/1000, и таким же образом двоичная дробь 0.001 имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное реальное отличие состоит в том, что первая записана в дробной записи с основанием 10, а вторая — с основанием 2.
К сожалению, большинство десятичных дробей не могут быть представлены точно как двоичные дроби. Следствием этого является то, что, как правило, вводимые десятичные числа с плавающей запятой аппроксимируются только двоичными числами с плавающей запятой, фактически сохраненными в машине.
Сначала проблему легче понять из базы 10. Рассмотрим дробь 1/3. Вы можете приблизить это как основную 10 фракцию: 0.3 или лучше, 0.33или лучше, 0.333 и так далее. Независимо от того, сколько цифр вы хотите записать, результат никогда не будет ровно 1/3.
Таким же образом, независимо от того, сколько цифр из 2-х оснований вы хотите использовать, десятичное значение 0,1 не может быть представлено в точности как дробь из 2-х оснований. В базе 2 1/10 — бесконечно повторяющаяся дробь 0.0001100110011001100110011...
Остановитесь на любом конечном количестве битов, и вы получите приближение. На большинстве современных машин числа с плавающей запятой аппроксимируются с использованием двоичной дроби, а числитель использует первые 53 бита, начиная с самого старшего бита, а знаменатель — как степень двух. В случае 3602879701896397/2 ** 55, что близко, но не точно равно истинному значению 1/10.
Многие пользователи не знают о приближении из-за способа отображения значений. Python печатает только десятичное приближение к истинному десятичному значению двоичного приближения, хранящегося на машине. На большинстве машин, если бы Python должен был печатать истинное десятичное значение двоичного приближения, хранящегося для 0. 1, он должен был бы отображать
1, он должен был бы отображать
>>> 0.1 # 0.1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считают полезным, поэтому Python сохраняет количество цифр управляемым, отображая округленное значение вместо
>>> 1 / 10 # 0.1
Просто помните, что хотя напечатанный результат выглядит как точное значение 1/10, фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что существует много разных десятичных чисел, которые имеют одну и ту же ближайшую приблизительную двоичную дробь. Например, числа 0.1 и 0.10000000000000001 и 0.1000000000000000055511151231... все приблизительно равны 3602879701896397/2 ** 55. Поскольку все эти десятичные значения имеют одинаковую аппроксимацию, любое из них может отображаться при сохранении инварианта
Исторически Python и встроенная функция repr() выбирали функцию с 17 значащими цифрами, 0.. Начиная с Python 3.1 в большинстве систем теперь может выбирать самый короткий из них и просто отображать 0.1. 10000000000000001
10000000000000001
Обратите внимание, что это по своей природе двоичное число с плавающей точкой: это не ошибка в Python и не ошибка в вашем коде. Вы увидите то же самое на всех языках, которые поддерживают арифметику с плавающей запятой.
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного числа значащих цифр:
>>> import math >>> format(math.pi, '.12g') # '3.14159265359' >>> format(math.pi, '.2f') # '3.14' >>> repr(math.pi) # '3.141592653589793'
Важно понимать, что в действительности это иллюзия: вы просто округляете отображение истинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не является точно 1/10, суммирование трех значений 0,1 может также не дать точно 0,3:
>>> 0.1 + 0.1 + 0.1 == 0.3 # False
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10, а 0,3 не может приблизиться к точному значению 3/10, предварительное округление функцией
>>> round(0.1, 1) + round(0.1, 1) + round(0.1, 1) == round(0.3, 1) # False
Двоичная арифметика с плавающей точкой содержит много сюрпризов, подобных этому. Проблема с 0.1 подробно объясняется в разделе «Ошибка представления». Смотрите также «Опасности с плавающей точкой» для более полного описания других распространенных сюрпризов.
Как говорится, «простых ответов нет». Тем не менее, не следует чрезмерно опасаться чисел с плавающей запятой! Ошибки в операциях с плавающей запятой Python наследуются от аппаратного обеспечения чисел с плавающей запятой, и на большинстве машин они имеют порядок не более одной части в
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования арифметики с плавающей запятой вы увидите ожидаемый результат в конце, если просто округлите отображение окончательных результатов до ожидаемого количества десятичных цифр.
str() обычно достаточно, и для более точного управления смотрите спецификаторы формата метода str.format().Для случаев использования, которые требуют точного десятичного представления, попробуйте использовать модуль decimal, который реализует десятичную арифметику, подходящую для приложений бухгалтерского учета и высокоточных приложений.
Другая форма точной арифметики поддерживается модулем fractions, который реализует арифметику, основанную на рациональных числах, поэтому числа, такие как 1/3 могут быть представлены точно.
Если вы большой пользователь операций с плавающей запятой, вам следует взглянуть на пакет Numeric Python и многие другие пакеты для математических и статистических операций, предоставляемых проектом SciPy.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите узнать точное значение числа с плавающей точкой. Метод
Метод float.as_integer_ratio() выражает значение типа float в виде дроби:
>>> x = 3.14159 >>> x.as_integer_ratio() # (3537115888337719, 1125899906842624)
Поскольку отношение является точным, оно может быть использовано для воссоздания исходного значения без потерь:
>>> x == 3537115888337719 / 1125899906842624 # True
Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном формате (основание 16), снова давая точное значение, сохраненное компьютером:
>>> x.hex() # '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для точного восстановления значения с плавающей точкой:
>>> x == float.fromhex('0x1.921f9f01b866ep+1')
True
Поскольку представление является точным, оно полезно для надежного переноса значений между различными версиями Python и обмена данными с другими языками, поддерживающими тот же формат, например Java.
Другим полезным инструментом является функция math.fsum(), которая помогает уменьшить потерю точности во время суммирования. Она отслеживает «потерянные цифры», когда значения добавляются в промежуточный итог. Это может повлиять на общую точность, так что ошибки не накапливаются до такой степени, что бы влиять на итоговую сумму:
>>> import math >>> sum([0.1] * 10) == 1.0 False >>> math.fsum([0.1] * 10) == 1.0 True
Ошибка представления.
0.1 и показано, как вы можете выполнить точный анализ подобных случаев самостоятельно. Предполагается базовое знакомство с двоичным представлением чисел с плавающей точкой.Ошибка представления относится к тому факту, что фактически большинство десятичных дробей не могут быть представлены точно как двоичные дроби (основание 2) . Это главная причина, почему Python или Perl, C, C++, Java, Fortran и многие другие языки часто не будут отображать точное десятичное число, которое ожидаете.
Это почему? 1/10 не совсем представимо в виде двоичной дроби. Почти все машины сегодня используют арифметику IEEE-754 с плавающей точкой, и почти все платформы отображают плавающие значения Python в IEEE-754 с «двойной точностью». При вводе, компьютер стремится преобразовать 0,1 в ближайшую дробь по форме J — целое число, содержащее ровно 53 бита.
Перепишем 1 / 10 ~= J / (2**N) как J ~= 2**N / 10 и напоминая, что J имеет ровно 53 бита, это >= 2**52, но < 2**53, наилучшее значение для N равно 56:
>>> 2**52 <= 2**56 // 10 < 2**53 # True
То есть 56 — единственное значение для N, которое оставляет J точно с 53 битами. Наилучшее возможное значение для J тогда будет округлено:
>>> q, r = divmod(2**56, 10) >>> r # 6
Поскольку остаток больше половины от 10, наилучшее приближение получается округлением вверх:
>>> q+1 # 7205759403792794
Поэтому наилучшее возможное приближение к 1/10 при двойной точности 754: 7205759403792794 / 2 ** 56. Деление числителя и знаменателя на два уменьшает дробь до:
Деление числителя и знаменателя на два уменьшает дробь до: 3602879701896397 / 2 ** 55
Обратите внимание, поскольку мы округлили вверх, то значение на самом деле немного больше, чем 1/10. Если бы мы не округлили, то значение был бы немного меньше 1/10. Но ни в коем случае это не может быть ровно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: то, что он видит, это точная дробь, указанная выше, наилучшее двоичное приближение 754, которое он может получить:
>>> 0.1 * 2 ** 55 # 3602879701896397.0
Если мы умножим эту дробь на 10 ** 55, мы увидим значение до 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 # 1000000000000000055511151231257827021181583404541015625
Это означает, что точное число, хранящееся в компьютере, равно десятичному значению полученному выше. Вместо отображения полного десятичного значения многие языки, включая более старые версии Python округляют результат до 17 значащих цифр:
>>> format(0.1, '.17f') '0.10000000000000001'
Модули fractions and decimal упрощают эти вычисления:
>>> from decimal import Decimal
>>> from fractions import Fraction
>>> Fraction.from_float(0.1)
# Fraction(3602879701896397, 36028797018963968)
>>> (0.1).as_integer_ratio()
# (3602879701896397, 36028797018963968)
>>> Decimal.from_float(0.1)
# Decimal('0.1000000000000000055511151231257827021181583404541015625')
>>> format(Decimal.from_float(0.1), '.17')
# '0.10000000000000001'
round Округляет заданное значение x в сторону ближайшего целого числа с округлением до четных значений. Особые случаи:
ceil() округляет заданное значение до ближайшего целого числа, большего, чем оно само. floor() округляет заданное значение до ближайшего целого числа, меньшего самого себя.
Мы можем использовать DecimalFormat(«0.00»), чтобы число всегда округлялось до 2 знаков после запятой.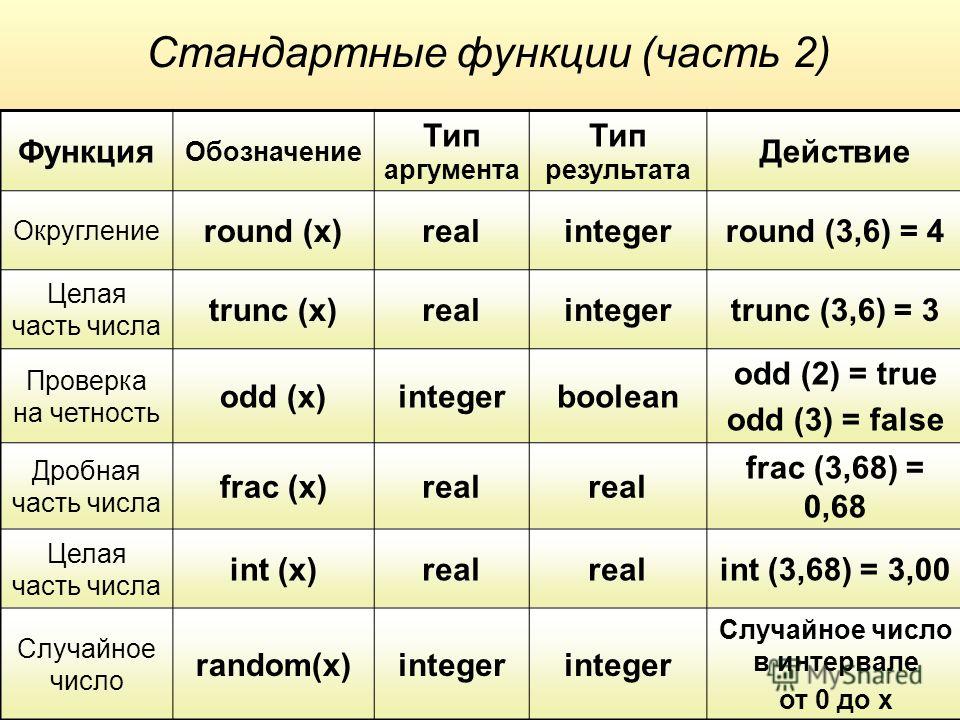
00 для округления до 2 знаков после запятой, если вы хотите округлить до 3 или 4 знаков, просто используйте #. 000 или #. 0000 для создания DecimalFormat. Чтобы узнать больше о форматировании чисел, см. Как форматировать числа в Java с помощью DecimalFormat.
kotlin-stdlib / kotlin.math / round
Требования к платформе и версии: JVM (1.2), JS (1.2), Native (1.2)
fun round(x: Double): Double
fun round(x: Float): Float
Округляет заданное значение x до ближайшего целого числа с округлением связей до четного целого числа.
Special cases:
-
round(x)являетсяx, гдеxявляетсяNaNили+Infили-Infили уже математическое целое число.
Kotlin 1.8
-
nextUp
Возвращает значение Double, ближайшее к этому в направлении положительной бесконечности.

-
pow
Возводит данное значение в степень x.
-
roundToInt
Округляет это значение Double до ближайшего целого числа и преобразует результат. Особые случаи: IllegalArgumentException, когда это значение NaN Округляет это значение с плавающей запятой
-
roundToLong
Округляет это значение Double до ближайшего целого числа и преобразует результат в Long.

- 1
- …
- 1199
- 1200
- 1201
- 1202
- 1203
- …
- 4091
- Next
404: Страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Поиск- Узнайте последние новости.
- Наша домашняя страница содержит самую свежую информацию о Java-разработке.
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, TheServerSide.com.
- Если вам нужно, свяжитесь с нами, мы будем рады услышать от вас.
Просмотр по категории
Архитектура приложения
- Прочная связь между законом Конвея и микросервисами
Хотя закон Конвея — это концепция, которой уже несколько десятков лет, некоторые утверждают, что спешка отрасли по внедрению микросервисов заставляет ее принимать …
- Как выжить, когда царит развитие Waterfall
Несмотря ни на что, методология Waterfall поддерживает бесчисленное количество команд разработчиков программного обеспечения.
 …
… - Необработанный, но растущий потенциал банковского обслуживания без ядра
Несмотря на то, что концепция банковского обслуживания без ядра все еще является новой концепцией, она демонстрирует большой потенциал для освобождения банков от жестких программных систем, которые…
Качество ПО
- Как сбалансировать доступ к данным и безопасность в финтех-тестировании
Использование реальных данных полезно при тестировании программного обеспечения, но команды должны быть осторожны, чтобы не поставить под угрозу безопасность и конфиденциальность. Шесть ядер…
- Тестовые фреймворки и примеры для модульного тестирования кода Python
Модульное тестирование является важным аспектом разработки программного обеспечения. Команды могут использовать Python для модульного тестирования, чтобы оптимизировать преимущества Python…

- Атрибуты эффективной стратегии тестирования базы данных
Команды должны внедрить правильную стратегию тестирования базы данных для оптимизации результатов. Изучите эффективные атрибуты тестирования базы данных…
Облачные вычисления
- Как работает маршрутизация на основе задержки в Amazon Route 53
Если вы рассматриваете Amazon Route 53 как способ уменьшить задержку, вот как работает этот сервис.
- 4 рекомендации, чтобы избежать привязки к поставщику облачных услуг
Без надлежащего планирования организация может оказаться в ловушке отношений с облачным провайдером. Следуйте этим …
- Подходит ли вам облачная стратегия?
Стратегия, ориентированная на облачные технологии, имеет свои преимущества и недостатки. Узнайте, как избежать рисков и построить стратегию, которая …
Безопасность
- 7 лучших инструментов предотвращения потери данных на 2023 год
Программное обеспечение для предотвращения потери данных является необходимостью для большинства компаний.
 Наше руководство дает вам краткий обзор семи ведущих поставщиков DLP …
Наше руководство дает вам краткий обзор семи ведущих поставщиков DLP … - Стандартизированные методы сбора данных могут помочь в борьбе с киберпреступностью
Внедрение стандартов, аналогичных NERC CIP, для всей индустрии кибербезопасности может облегчить правоохранительным органам…
- Mandiant: в 2022 году 63% взломов были обнаружены извне
В Mandiant заявили, что на увеличение в 2022 году, скорее всего, повлияло то, что фирма по анализу угроз активно расследует активность угроз…
ПоискAWS
- AWS Control Tower стремится упростить управление несколькими учетными записями
Многие организации изо всех сил пытаются управлять своей огромной коллекцией учетных записей AWS, но Control Tower может помочь. Услуга автоматизирует…
- Разбираем модель ценообразования Amazon EKS
В модели ценообразования Amazon EKS есть несколько важных переменных.
 Покопайтесь в цифрах, чтобы убедиться, что вы развернули службу…
Покопайтесь в цифрах, чтобы убедиться, что вы развернули службу… - Сравните EKS и самоуправляемый Kubernetes на AWS
Пользователи
AWS сталкиваются с выбором при развертывании Kubernetes: запустить его самостоятельно на EC2 или позволить Amazon выполнить тяжелую работу с помощью EKS. См…
Проблемы и ограничения — документация по Python 3.11.3
Числа с плавающей запятой представлены в аппаратном обеспечении компьютера как основание 2 (двоичное)
дроби. Например, десятичная дробная 0,125 имеет значение 1/10 + 2/100 + 5/1000, и таким же образом двоичная дробь 0,001 имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное
реальная разница в том, что первый записан в дробной системе счисления по основанию 10,
а второй в базе 2.
К сожалению, большинство десятичных дробей не могут быть точно представлены в двоичном виде. дроби. Следствием этого является то, что, как правило, десятичное число с плавающей запятой
числа, которые вы вводите, только аппроксимируются двоичными числами с плавающей запятой
фактически хранится в машине.
дроби. Следствием этого является то, что, как правило, десятичное число с плавающей запятой
числа, которые вы вводите, только аппроксимируются двоичными числами с плавающей запятой
фактически хранится в машине.
Задачу легче понять сначала в десятичной системе счисления. Рассмотрим дробь 1/3. Вы можете аппроксимировать это как десятичную дробь:
.или лучше
или лучше
и так далее. Независимо от того, сколько цифр вы готовы записать, результат никогда не будет ровно 1/3, но будет все более и более лучшим приближением к 1/3.
Таким же образом, независимо от того, сколько цифр с основанием 2 вы хотите использовать, десятичное значение 0,1 не может быть представлено точно как дробь с основанием 2. В базе 2, 1/10 — бесконечно повторяющаяся дробь
0.0001100110011001100110011001100110011001100110011...
Остановитесь на любом конечном числе битов, и вы получите приближение. На большинстве
современных машинах числа с плавающей запятой аппроксимируются с помощью двоичной дроби с
числитель, использующий первые 53 бита, начиная со старшего бита и
со знаменателем как степень двойки. В случае 1/10 двоичная дробь
это
В случае 1/10 двоичная дробь
это 3602879701896397 / 2 ** 55 , что близко, но не совсем
равно истинному значению 1/10.
Многие пользователи не знают об аппроксимации из-за того, как значения отображается. Python печатает только десятичное приближение к истинному десятичному значение двоичной аппроксимации, сохраненное машиной. На большинстве машин, если Python должен был печатать истинное десятичное значение сохраненного двоичного приближения. для 0.1 он должен отображать
>>> 0,1 0,1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считает нужным, поэтому Python сохраняет это число. цифр, управляемых отображением округленного значения вместо
>>> 1 / 10 0,1
Просто помните, даже если напечатанный результат выглядит как точное значение 1/10 фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что есть много разных десятичных чисел, которые имеют одинаковые
ближайшая приближенная двоичная дробь. Например, числа
Например, числа 0,1 и 0,10000000000000001 и 0.1000000000000000055511151231257827021181583404541015625 все
округляется на 3602879701896397/2**55 . Поскольку все эти десятичные
значения имеют одинаковое приближение, любое из них может быть отображено
сохраняя при этом инвариант eval(repr(x)) == x .
Исторически, приглашение Python и встроенная функция repr() выбирали
тот, у которого 17 значащих цифр, 0.10000000000000001 . Начиная с
Python 3.1, Python (в большинстве систем) теперь может выбирать самый короткий из
эти и просто отображать 0,1 .
Обратите внимание, что это заложено в самой природе двоичных чисел с плавающей запятой: это не ошибка.
в Python, и это также не ошибка в вашем коде. Вы увидите такой же
вещь на всех языках, которые поддерживают арифметику с плавающей запятой вашего оборудования
(хотя некоторые языки могут не отображать разницу по умолчанию или во всех
режимы вывода).
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного количества значащих цифр:
>>> format(math.pi, '.12g') # дать 12 значащих цифр '3.14159265359' >>> format(math.pi, '.2f') # указать 2 цифры после точки «3.14» >>> repr(math.pi) '3.141592653589793'
Важно понимать, что это в действительности иллюзия: вы просто округляя отображаем истинного машинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не совсем 1/10, суммирование трех значений 0,1 также может не дать ровно 0,3:
>>> .1 + .1 + .1 == .3 ЛОЖЬ
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10 и
0,3 не может приблизиться к точному значению 3/10, тогда предварительное округление с функция round() не может помочь:
>>> раунд(.1, 1) + раунд(.1, 1) + раунд(.1, 1) == раунд(.3, 1) ЛОЖЬ
Хотя числа нельзя приблизить к их предполагаемым точным значениям,
функция round() может быть полезна для последующего округления, так что результаты
с неточными значениями становятся сравнимыми друг с другом:
>>> раунд(.1 + .1 + .1, 10) == раунд(.3, 10) Истинный
Двоичная арифметика с плавающей запятой таит в себе много подобных сюрпризов. Проблема с «0,1» подробно объясняется ниже, в разделе «Ошибка представления». раздел. См. Опасности с плавающей запятой для более полного описания других распространенных сюрпризов.
Как сказано в конце, «простых ответов не бывает». Тем не менее, не будьте чрезмерно опасайтесь чисел с плавающей запятой! Ошибки в операциях Python с плавающей запятой наследуются от оборудования с плавающей запятой, и на большинстве машин порядка нет более 1 части в 2**53 за операцию. Этого более чем достаточно для большинства задачи, но нужно иметь в виду, что это не десятичная арифметика и что каждая операция с плавающей запятой может привести к новой ошибке округления.
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования операций с плавающей запятой
арифметики вы увидите результат, который вы ожидаете в конце, если вы просто округлите
отображение ваших окончательных результатов до ожидаемого количества десятичных цифр. Обычно достаточно
Обычно достаточно str() , а для более точного контроля см. str.format() спецификаторы формата метода в синтаксисе строки формата.
Для случаев использования, требующих точного десятичного представления, попробуйте использовать decimal Модуль , который реализует десятичную арифметику, подходящую для
бухгалтерские приложения и высокоточные приложения.
Другая форма точной арифметики поддерживается модулем дробей .
который реализует арифметику, основанную на рациональных числах (такие числа, как
1/3 можно представить точно).
Если вы интенсивно используете операции с плавающей запятой, вам следует взглянуть
в пакете NumPy и многих других пакетах для математических и
статистические операции, предоставляемые проектом SciPy. См.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно do хотите узнать точное значение числа с плавающей запятой.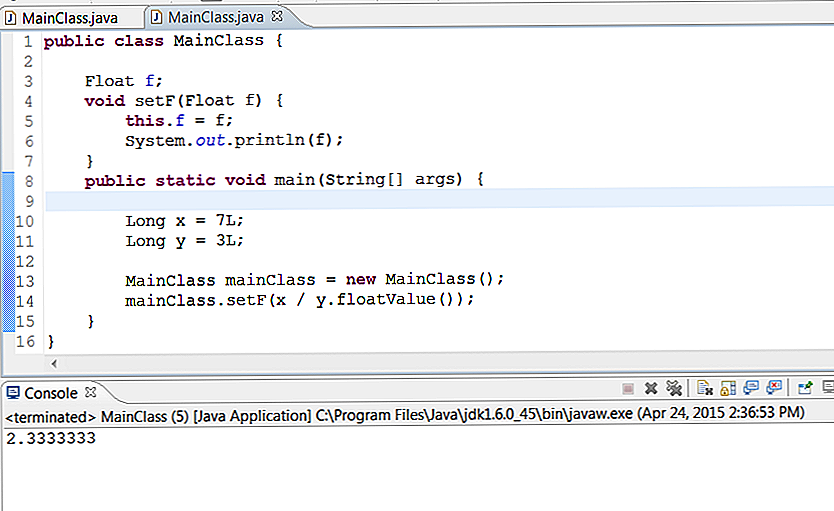
Метод float.as_integer_ratio() выражает значение числа с плавающей запятой в виде
дробь:
>>> х = 3,14159 >>> x.as_integer_ratio() (3537115888337719, 1125899906842624)
Поскольку соотношение является точным, его можно использовать для воссоздания без потерь исходное значение:
>>> х == 3537115888337719 / 1125899906842624 Истинный
Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном (базовое
16), снова давая точное значение, сохраненное вашим компьютером:
>>> x.hex() '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для восстановления значение с плавающей запятой точно:
>>> x == float.fromhex('0x1.921f9f01b866ep+1')
Истинный
Поскольку представление точное, оно полезно для надежного переноса значений
между различными версиями Python (независимость от платформы) и обмен
данные с другими языками, которые поддерживают тот же формат (например, Java и C99).
Еще один полезный инструмент — math.fsum() функция, которая помогает смягчить
потеря точности при суммировании. Он отслеживает «потерянные цифры» по мере того, как значения
добавляется к нарастающей сумме. Это может повлиять на общую точность
чтобы ошибки не накапливались до такой степени, что они влияют на
окончательный итог:
>>> сумма([0.1] * 10) == 1.0 ЛОЖЬ >>> math.fsum([0.1] * 10) == 1.0 Истинный
В этом разделе подробно объясняется пример «0.1» и показано, как можно выполнить точный анализ подобных случаев самостоятельно. Базовое знакомство с бинарником предполагается представление с плавающей запятой.
Ошибка представления относится к тому факту, что некоторые (фактически большинство)
десятичные дроби не могут быть представлены точно как двоичные дроби (с основанием 2).
Это главная причина, по которой Python (или Perl, C, C++, Java, Fortran и многие другие)
другие) часто не будет отображать точное десятичное число, которое вы ожидаете.
Почему? 1/10 нельзя точно представить в виде двоичной дроби. Почти все машины сегодня (ноябрь 2000 г.) используют арифметику с плавающей запятой IEEE-754, и почти все платформы отображают Python с плавающей запятой в соответствии с IEEE-754 «двойной точностью». 754 числа double содержат 53 бита точности, поэтому при вводе компьютер стремится преобразовать 0,1 в ближайшую дробь, которую он может иметь в форме J /2** N где J целое число, содержащее ровно 53 бита. Переписывание
1 / 10 ~= Дж / (2**Н)
как
Дж ~= 2**Н/10
и вспоминая, что J имеет ровно 53 бита ( >= 2**52 , но < 2**53 ),
лучшее значение для N 56:
>>> 2**52 <= 2**56 // 10 < 2**53 Истинный
То есть 56 — единственное значение для N , которое оставляет J ровно с 53 битами. наилучшее возможное значение для J - это округленное частное:
>>> q, r = divmod(2**56, 10) >>> г 6
Поскольку остаток больше половины от 10, получается наилучшее приближение округляя:
>>> д+1 7205759403792794
Следовательно, наилучшее возможное приближение к 1/10 в 754 с двойной точностью:
7205759403792794/2**56
Деление числителя и знаменателя на два уменьшает дробь до:
3602879701896397/2**55
Обратите внимание, что, поскольку мы округлили, на самом деле это немного больше, чем 1/10;
если бы мы не округляли, то частное было бы немного меньше, чем
1/10. Но ни в коем случае не может быть именно 1/10!
Но ни в коем случае не может быть именно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: он видит точную заданную дробь. выше, лучшее 754 двойное приближение, которое он может получить:
>>> 0,1 * 2 ** 55 3602879701896397.0
Если мы умножим эту дробь на 10**55, мы увидим значение, равное 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 1000000000000000055511151231257827021181583404541015625
означает, что точное число, хранящееся в компьютере, равно десятичное значение 0,1000000000000000055511151231257827021181583404541015625. Вместо отображения полного десятичного значения многие языки (включая более старые версии Python), округлить результат до 17 значащих цифр:
>>> формат (0.1, '.17f') «0,10000000000000001»
дроби и десятичные модули делают эти расчеты
легко:
>>> из десятичного импорта Decimal >>> из дробей импорт дроби >>> Дробь.

 1, 1) + round(0.1, 1) + round(0.1, 1) == round(0.3, 1)
# False
1, 1) + round(0.1, 1) + round(0.1, 1) == round(0.3, 1)
# False
 1, '.17f')
'0.10000000000000001'
1, '.17f')
'0.10000000000000001'


 …
…
 Наше руководство дает вам краткий обзор семи ведущих поставщиков DLP …
Наше руководство дает вам краткий обзор семи ведущих поставщиков DLP … Покопайтесь в цифрах, чтобы убедиться, что вы развернули службу…
Покопайтесь в цифрах, чтобы убедиться, что вы развернули службу… 1 + .1 + .1, 10) == раунд(.3, 10)
Истинный
1 + .1 + .1, 10) == раунд(.3, 10)
Истинный
