#11. Произведение матриц и векторов, элементы линейной алгебры

Смотреть материал на видео

Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую: 

a = np.arange(1, 10).reshape(3, 3)
b = np.arange(10, 19).reshape(3, 3)
a*b

В консоли увидим результат:

array([[ 10,  22,  36],
       [ 52,  70,  90],
[112, 136, 162]])

Матричное умножение

Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:

то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду: 

np. dot(a, b)

Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:

array([[ 84,  90,  96],
[201, 216, 231],
[318, 342, 366]])

Тот же результат можно получить и с помощью функции: 

np.matmul(a, b)

Считается, что этот вариант предпочтительнее использовать при умножении матриц.

Векторное умножение

Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:

то их умножение можно реализовать в двух видах:

и

Первое умножение реализуется либо через функцию: 

a = np.arange(1, 10)
b = np.ones(9)
np.dot(a, b) # значение 45

Либо, более предпочтительной функцией для внутреннего умножения векторов: 

np. inner(a, b) # 45

Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции: 

np.outer(a, b)

получим результат в виде следующей матрицы:

array([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
       [2., 2., 2., 2., 2., 2., 2., 2., 2.],

       [3., 3., 3., 3., 3., 3., 3., 3., 3.],
       [4., 4., 4., 4., 4., 4., 4., 4., 4.],
       [5., 5., 5., 5., 5., 5., 5., 5., 5.],
       [6., 6., 6., 6., 6., 6., 6., 6., 6.],
       [7., 7., 7., 7., 7., 7., 7., 7., 7.],
       [8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])

Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul: 

a @ b # значение 45

или, с использованием матриц: 

a. resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b)

Умножение вектора на матрицу

Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:

или

Для реализации первого способа, зададим одномерный вектор и двумерную матрицу: 

a = np.array([1,2,3])
b = np.arange(4,10).reshape(3,2) # матрица 3x2

И, затем, воспользуемся уже знакомой нам функцией dot: 

np.dot(a, b) # array([40, 46])

При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.

Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку: 

np.dot(b, a) # несогласованность размеров

Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:

Определим массивa в два элемента и умножим на матрицу b: 

a = np. array([1, 2])
np.dot(b, a) # array([14, 20, 26])

Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде: 

a.shape = -1, 1 # вектор-столбец 2x1

Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец: 

np.dot(b, a) # вектор-столбец 3x1

Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul): 

a @ b # вектор-столбец 3x1

Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.

Элементы линейной алгебры

Из высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций.

Предположим, имеется квадратная матрица 3×3: 

a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])

Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов: 

np.linalg.matrix_rank(a) # рангравен 3

Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:

Здесь  - некие числа линейного уравнения. Например, возьмем их равными: 

y = np.array([10, 20, 30])

Тогда корни уравнения можно вычислить с помощью функции solve: 

np.linalg.solve(a, y) # array([-5.  , 10.   , -1.66666667])

Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы.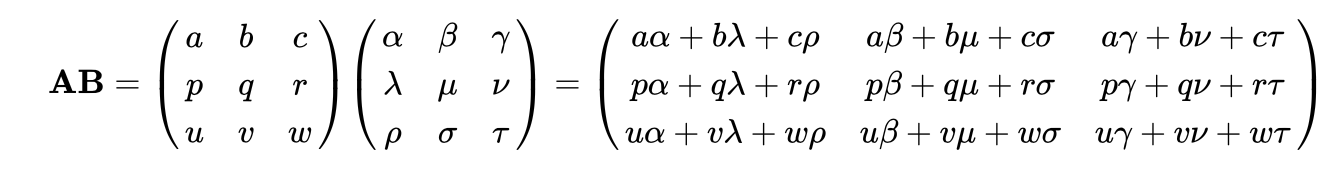 Изначально, уравнение можно записать в векторно-матричном виде:

Откуда получаем решения :

На уровне пакета NumPy это делается так: 

invA = np.linalg.inv(a) # вычисление обратной матрицы
invA @ y # вычисление корней

Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.

Функция

Описание

linalg.cholesky()

Разложение Холецкого

linalg.

qr()

QR-разложение матрицы

linalg.svd()

Сингулярное (SVD) разложение матрицы

linalg.norm()

Норма матрицы или вектора

linalg.cond()

Число обусловленности матрицы

linalg.det()

Определитель (детерминант) матрицы

linalg.matrix_rank()

Вычисление ранга матрицы по алгоритму SVD

np.trace()

Сумма диагональных элементов массива

linalg. eig()

Вычисление собственных значений и правых собственных векторов

linalg.eigvals()

Вычисление собственных значений матрицы

linalg.solve()

Решение линейного матричного уравнения

linalg.tensorsolve()

Решение линейного тензорного уравнения

linalg.lstsq()

Решает задачу поиска наименьших квадратов для линейного матричного уравнения

linalg.inv()

Вычисление обратной матрицы

linalg. pinv()

Вычисление псевдообратной (Мура-Пенроуза) матрицы

linalg.tensorinv()

Вычисление обратного тензора (N-мерного массива)

Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:

https://numpy.org/doc/stable/

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6.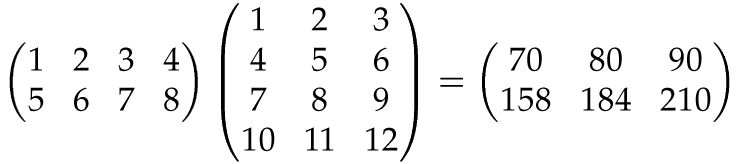 Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

Векторы и матрицы в инструментарии Numpy

Рубрика: 14 Инструментарий Numpy на языке PythonАвтор: Андрей Никитенко

Содержание страницы

  • 1 Векторы и матрицы
  • 2 Создание матриц для работы с ними
  • 3 Произведение матриц
  • 4 Другие операции с матрицами
  • 5 Решение системы линейных уравнений
  • 6 Текстовая задача

Векторы и матрицы

Здравствуйте и вновь добро пожаловать на занятия по теме «Инструментарий Numpy на языке Python».

В этой статье мы подробнее рассмотрим векторы, а также поговорим о матрицах.

Вы уже видели, насколько массивы Numpy похож на векторы: мы можем проводить над ними такие операции, как их сложение, умножение на скаляр, выполнять поэлементные операции вроде возведения в квадрат. А что с матрицами? Матрицу можно рассматривать как двухмерный массив. Согласно другому представлению, её также можно рассматривать как список списков. Действительно, можно использовать список списков, чтобы определить матрицу. Попробуем так и сделать.

Итак,первый список будет иметь элементы 1 и 2, второй список – элементы 3 и 4.Обратите внимание, что списки должны иметь одинаковую длину.

M = np.array([ [1,2], [3,4] ])

Считается,что первый индекс – это строка, второй – столбец. Для сравнения создадим такженастоящий список списков:

L = [ [1,2], [3,4] ]

Допустим,мы хотим получить элемент матрицы, скажем, единицу. В списке Python сначала индексируется строка, что даёт нам первыйсписок, содержащий 1 и 2:

L[0]

Итак,теперь у нас есть 1 и 2. Нам нужен первый элемент из этого списка, поэтому

L[0][0]

и получаем 1. Заметьте, то же самое можно сделать ис помощью массива Numpy:

M[0][0]

Этотакже даёт нам 1. Но есть и сокращённая запись, похожая на MATLAB, с использованием запятой:

M[0,0]

Иэто также даёт нам 1. Так несколько удобнее, поскольку нужно набрать на символменьше.

Обратитевнимание, что в Numpy есть типданных, который так и называется – матрица:

M2 = np.matrix([ [1,2], [3,4] ])

Получиласьматрица. Во многом матрица схожа с массивом Numpy,но есть и отличия. В большинстве случаев используются просто массивы Numpy; в действительности даже официальная документацияфактически рекомендует не пользоваться матрицами. Поэтому в данном курсе мы небудем заострять на них своё внимание. Увидев матрицу, имеет смысл преобразоватьеё в массив. Это можно сделать с помощью команды

A = np.array(M2)

Врезультате получим ту же матрицу, но в виде массива. Обратите внимание, что,хоть это и массив, мы можем пользоваться удобными матричными операциями, напримертранспонированием:

A.T

Врезультате получается транспонированная матрица A.

Резюмируем. Мы показали, что матрица на самом деле является лишь двухмерным массивом Numpy, а вектор – одномерным массивом Numpy. Таким образом, матрица на самом деле является двухмерным вектором. Обобщая, можно считать матрицу двухмерным математическим объектом, содержащим числа, а вектор – одномерным математическим объектом, также содержащим числа. Иногда встречается представление вектора в виде двухмерного объекта. Например, в учебниках по математике может указываться вектор-столбец размерности 3×1 и вектор-строка размерности 1×3. Временами мы также будем представлять их в таком виде в Numpy, но наличие двух размерностей делает такой объект более похожим на матрицу, что может сбить с толку. В таком случае просто помните, что обсуждаются лишь две вещи – одномерные и двухмерные массивы.

Создание матриц для работы с ними

Существуют некоторые различные способы генерации массивов данных.

Иногда нужны несколько массивов просто чтобы попрактиковаться – как в этом курсе. Один из способов вы уже видели, когда я воспользовался массивом Numpy для создания списка, например

np.array([1,2,3])

Заметьте,это не очень удобно, поскольку приходится вручную вставлять каждый элемент. Аесли нужен массив с сотней элементов? А если нужно, чтобы он содержал случайныечисла? Поэтому в данной лекции будет показано, как можно создавать массивы.

Преждевсего я покажу, как создать массив, состоящих из одних нулей. Это делается спомощью функции zeros с указаниемдлины:

Z = np.zeros(10)

Этодаёт вектор с 10 элементами, состоящий из нулей. Можно создать и матрицуразмерности 10×10, состоящую из одних нулей:

Z = np.zeros((10, 10))

Врезультате получаем 100 нулей в матрице размерности 10×10. Обратите внимание, что функция по-прежнему принимает лишь один аргумент – кортеж,содержащий каждую размерность. Есть эквивалентная функция, создающая массив изодних единиц. К примеру,

O = np.ones((10, 10))

Получиласьматрица размерности 10×10, состоящая изодних единиц.

Теперь предположим, что нам нужен ряд случайных числен. Для этого можно воспользоваться функцией np.random.random. Создадим, к примеру, массив случайных чисел размерности 10×10:

R = np.random.random((10,10))

Получилсянабор случайных чисел в матрице размерностью 10×10.Бросается в глаза, что все числа больше 0 и меньше 1. Это связано с тем, чтокогда речь идёт о случайных числах, имеется в виду распределение вероятностей,откуда и возникли случайные числа. Данная конкретная функция случайных чиселдаёт нам равномерно распределённые числа между 0 и 1. А если нам нужны числа сгауссовым распределением? В Numpy есть функция идля этого. Давайте попробуем. Называется она random.randn. Вновь-таки, возьмём размерность 10×10:

G = np.random.randn((10×10))

И у нас ничего не получилось – требуются целые числа. Сама функция правильна, но мы указали неправильный аргумент. Дело в том, что, как ни странно, функция randn библиотеки Numpy воспринимает каждую размерность как отдельный аргумент, в то время как все остальные упоминавшиеся функции принимают кортежи. Поэтому правильно вставлять – только для функции randn! – каждую размерность по отдельности:

G = np.random.randn(10,10)

Теперьвсё работает. Мы имеем числа с гауссовым распределением, средним значением 0 идисперсией 1. Массивы Numpy такжепредоставляют удобные функции для вычисления этих статистических величин. Так,команда

G.mean()

даёт нам среднее значение, а команда

G.var()

позволяет получить дисперсию.

Как видим, полученные числа весьма близки к истинным значениям.

Произведение матриц

Чтоинтересно в произведениях матриц при изучении линейной алгебры, – так это то, чтообычно называется умножением матриц. Умножение матриц имеет специальноетребование: внутренние размерности двух умножаемых матриц должны совпадать.Так, если у нас есть матрица A размерности 2×3и матрица Bразмерности 3×3, то мы можем умножить A на B, поскольку внутренняя размерность равна 3. Однакомы не можем умножить B на A, поскольку внутренняя размерность левого множителяравна 3, а внутренняя размерность правого равна 2.

Возникаетвопрос: для чего существует такое требование при умножении матриц? Рассмотримопределение операции умножения матриц:

Тоесть ij-йэлемент матрицы Cравен сумме произведений всех соответствующих элементов из i-й строкиматрицы Aи j-гостолбца матрицы B.Другими словами, ij-йэлемент матрицы Cравен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:

C = A.dot(B)

Этои будет умножением матриц.

Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*). Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.

Другие операции с матрицами

В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.

Начнёмс нахождения обратной матрицы. Вначале создадим матрицу:

A = np.array([[1,2],[3,4]])

Воспользуемсяфункцией inv модуля linalg:

Ainv = np.linalg.inv(A)

Мыполучили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу,обратную A,на саму А:

Ainv.dot(A)

Врезультате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:

A.dot(Ainv)

Итоже получаем единичную матрицу.

Следующее– нахождение определителя матрицы. Это можно сделать с помощью команды

np.linalg.det(A)

Каки ожидалось, получаем ответ -2.

Иногданужна диагональ матрицы, для этого используется команда

np.diag(A)

Врезультате имеем диагональные элементы в виде вектора. В других случаях у насесть вектор чисел, представляющий диагональ матрицы, остальные элементы которойсчитаются равными нулю. Чтобы представить такой вектор в виде двухмерногомассива, можно воспользоваться этой же функцией. Например,

np.diag([1,2])

Получим1 и 2 на диагонали, а остальные элементы – нули.

Этонадо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональныхэлементов; если же подставить одномерный массив, то получится двухмерныймассив, в котором все внедиагональные элементы равны нулю, а первоначальныймассив располагается на главной диагонали матрицы.

Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.

Итак,создадим два вектора:

a = np.array([1,2])

b = np.array([3,4])

Внешнеепроизведение вычисляется по команде

np.outer(a, b)

Можетепроверить правильность ответа. Обратите внимание, что можно выполнить ивнутреннее произведение с помощью команды

np.inner(a, b)

Этодаст тот же ответ, что и при использовании команды

a.dot(b)

Какимиз этих способов пользоваться – сугубо на ваше усмотрение.

Другаяраспространённая операция – нахождение следа матрицы. Это сумма элементовматриц, расположенных на главной диагонали. Заметьте, что мы можем выполнитьэту операцию, используя уже имеющиеся сведения:

np. dialog(A).sum()

Получиможидаемый ответ 5. Но в Numpy для этого естьи соответствующая функция:

np.trace(A)

Имы опять-таки получаем 5.

Ипоследнее, что мы обсудим, – это собственные значения и собственные векторы.Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следуетуглубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делаетсяв коде, поэтому если вы не знаете, что такое собственные значения и собственныевекторы, просто пропустите эту часть.

Частовозникает необходимость вычислить собственные значения и собственные векторысимметричной матрицы, такой как ковариационная матрица набора данных. Создадимслучайным образом определённые данные размерности 100×3с гауссовым распределением:

X = np.random.randn(100,3)

Обратитевнимание: считается, что каждый пример – это строка, а каждый признак – этостолбец, поэтому для данного конкретного вымышленного набора данных у насимеется 100 примеров и 3 признака. Разумеется, в Numpyуже есть функция для вычисления ковариации. Опробуем её:

cov = np.cov(X)

Проверимразмерность ковариационной матрицы, чтобы убедиться, что всё правильно.

cov.shape

Получилось,что размерность равна 100×100. Этонеправильная размерность, должно быть 3×3,ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:

cov = np.cov(X.T)

Теперьразмерность 3×3. Нужно помнить, что при вычислении ковариационнойматрицы данных необходимо её сначала транспонировать.

Длявычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовыхматриц. Если вы никогда не изучали линейную алгебру комплексных чисел, небеспокойтесь о том, что такое эрмитова матрица. Симметричной называетсяматрица, которая, будучи транспонированной, остаётся равной сама себе:

Тоесть ij-йэлемент матрицы Cравен сумме произведений всех соответствующих элементов из i-й строкиматрицы Aи j-гостолбца матрицы B. Другими словами, ij-йэлемент матрицы Cравен скалярному произведению i-й строки матрицы A и j-го столбца матрицы B. В связи с этим обычно используется функция dot библиотеки Numpy:

C = A.dot(B)

Этои будет умножением матриц.

Как в математике, так и в программировании часто встречается операция поэлементного умножения. В случае векторов мы уже видели, что для этого используется звёздочка (*). Как можно догадаться, в случае двухмерных массивов звёздочка также производит поэлементное умножение. Это означает, что при использовании звёздочки в случае многомерных массивов оба массива должны иметь в точности одинаковую размерность. Это может показаться странным, ведь в других языках звёздочка действительно означает настоящее умножение матриц. Но нужно просто запомнить, что для Numpy звёздочка означает поэлементное умножение, а функция dot – умножение матриц. Также сбивать с толку может то обстоятельство, что при записи математических уравнений нет даже чётко определённого символа для операции поэлементного умножения. Так, некоторые пользуются кружком с точкой внутри, а некоторые – кружком с крестиком внутри. Похоже, в математике просто не существует стандартной записи для данной операции, хотя она часто возникает в машинному обучении в связи с необходимостью использовать градиенты.

Другие операции с матрицами

В данном подразделе, я покажу вам некоторые другие операции с матрицами, которые позволяет библиотека Numpy. При этом предполагается, что вы уже знакомы с ними из курса линейной алгебры, а потому это будет скорее демонстрация того, как их реализовать в Numpy.

Начнёмс нахождения обратной матрицы. Вначале создадим матрицу:

A = np.array([[1,2],[3,4]])

Воспользуемсяфункцией inv модуля linalg:

Ainv = np.linalg.inv(A)

Мыполучили обратную матрицу. Чтобы проверить правильность ответа, умножим матрицу,обратную A,на саму А:

Ainv.dot(A)

Врезультате имеем единичную матрицу. Можем сделать и наоборот, умножив матрицу А на обратную ей:

A.dot(Ainv)

Итоже получаем единичную матрицу.

Следующее– нахождение определителя матрицы. Это можно сделать с помощью команды

np.linalg.det(A)

Каки ожидалось, получаем ответ -2.

Иногданужна диагональ матрицы, для этого используется команда

np.diag(A)

Врезультате имеем диагональные элементы в виде вектора. В других случаях у насесть вектор чисел, представляющий диагональ матрицы, остальные элементы которойсчитаются равными нулю. Чтобы представить такой вектор в виде двухмерногомассива, можно воспользоваться этой же функцией. Например,

np.diag([1,2])

Получим1 и 2 на диагонали, а остальные элементы – нули.

Этонадо запомнить: если подставить двухмерный массив в функцию diag, то получим одномерный массив из диагональныхэлементов; если же подставить одномерный массив, то получится двухмерныймассив, в котором все внедиагональные элементы равны нулю, а первоначальныймассив располагается на главной диагонали матрицы.

Бывает, что у нас есть два вектора, а нам нужно выполнить внешнее произведение. В частности, внешнее произведение возникает, когда мы вычисляем ковариацию ряда векторов-образцов. Мы уже знакомы с поэлементным произведением, для которого используется звёздочка, и скалярным произведением, для чего используется функция dot. Напомню, что скалярное произведение также называется внутренним произведением.

Итак,создадим два вектора:

a = np.array([1,2])

b = np.array([3,4])

Внешнеепроизведение вычисляется по команде

np.outer(a, b)

Можетепроверить правильность ответа. Обратите внимание, что можно выполнить ивнутреннее произведение с помощью команды

np.inner(a, b)

Этодаст тот же ответ, что и при использовании команды

a.dot(b)

Какимиз этих способов пользоваться – сугубо на ваше усмотрение.

Другаяраспространённая операция – нахождение следа матрицы. Это сумма элементовматриц, расположенных на главной диагонали. Заметьте, что мы можем выполнитьэту операцию, используя уже имеющиеся сведения:

np.dialog(A).sum()

Получиможидаемый ответ 5. Но в Numpy для этого естьи соответствующая функция:

np.trace(A)

Имы опять-таки получаем 5.

Ипоследнее, что мы обсудим, – это собственные значения и собственные векторы.Если вы не проходили их в курсе линейной алгебры, то, вероятно, вам следуетуглубить свои знания по этому предмету. Но сейчас я просто покажу, как всё это делаетсяв коде, поэтому если вы не знаете, что такое собственные значения и собственныевекторы, просто пропустите эту часть.

Частовозникает необходимость вычислить собственные значения и собственные векторысимметричной матрицы, такой как ковариационная матрица набора данных. Создадимслучайным образом определённые данные размерности 100×3с гауссовым распределением:

X = np.random.randn(100,3)

Обратитевнимание: считается, что каждый пример – это строка, а каждый признак – этостолбец, поэтому для данного конкретного вымышленного набора данных у насимеется 100 примеров и 3 признака.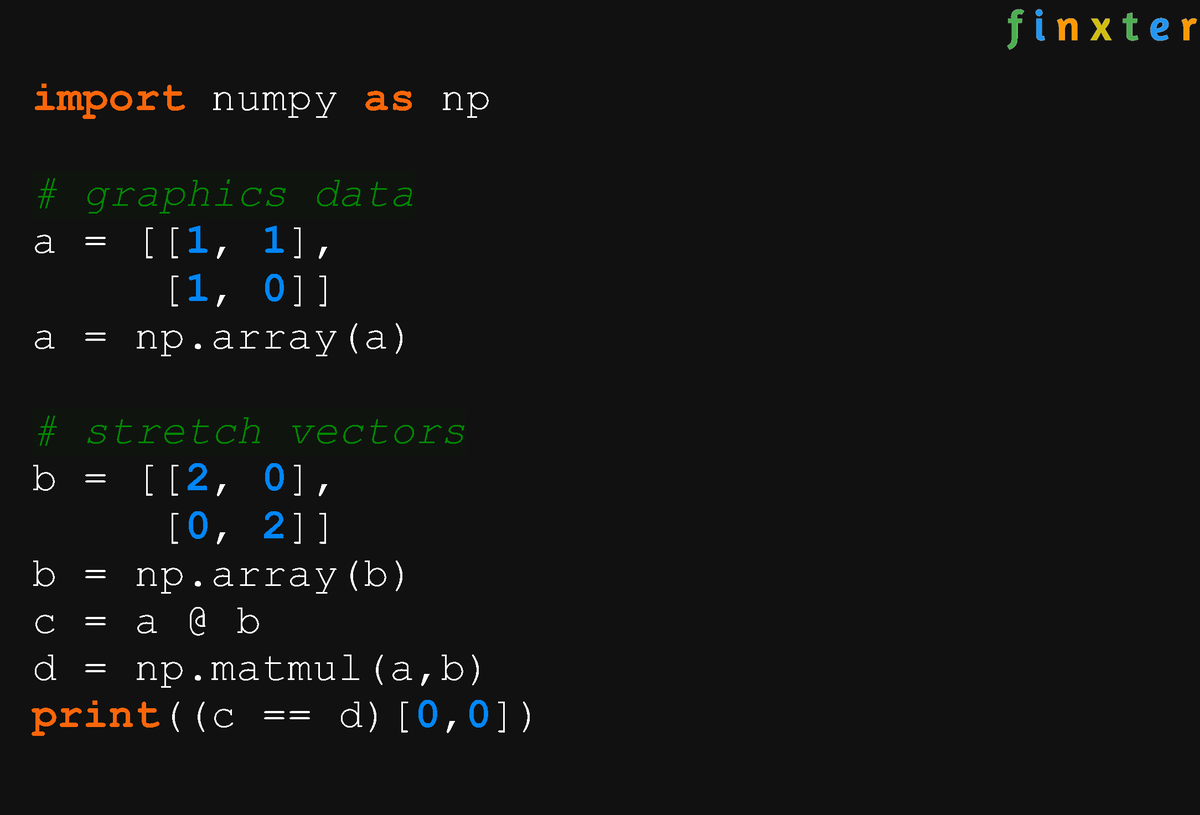 Разумеется, в Numpyуже есть функция для вычисления ковариации. Опробуем её:

cov = np.cov(X)

Проверимразмерность ковариационной матрицы, чтобы убедиться, что всё правильно.

cov.shape

Получилось,что размерность равна 100×100. Этонеправильная размерность, должно быть 3×3,ведь наши данные имеют размерность 3. Попробуем ещё раз, транспонировав X:

cov = np.cov(X.T)

Теперьразмерность 3×3. Нужно помнить, что при вычислении ковариационнойматрицы данных необходимо её сначала транспонировать.

Длявычисления собственных значений и собственных векторов есть две функции – eig и eigh. Eigh предназначена только для симметричных и эрмитовыхматриц. Если вы никогда не изучали линейную алгебру комплексных чисел, небеспокойтесь о том, что такое эрмитова матрица. Симметричной называетсяматрица, которая, будучи транспонированной, остаётся равной сама себе:

Эрмитова же матрица – это матрица, которая остаётся равной сама себе, будучи сопряжённой:

Какизвестно, ковариационная матрица является симметричной, поэтому можноиспользовать функцию eigh. Её ипопробуем:

np.linalg.eigh(cov)

Врезультате получаем кортежи. Первый содержит три собственных значения, а второй– собственные векторы, представленные в столбцах. Попробуем теперь с обычнойфункцией eig:

np.linalg.eig(cov)

Получаемтот же ответ. Обратите внимание, что обычная функция eigхоть и даёт тот же ответ, но полученные собственные значения и соответствующиесобственные векторы могут размещаться в другом порядке. В данном конкретномслучае порядок тот же, но есть вероятность, что он может поменяться.

На этом лекция заканчивается. Она довольно короткая, поскольку была создана для тех, кто уже знаком с математическим аппаратом, но ещё не знает, как его реализовать в Numpy.

Решение системы линейных уравнений

В заключение мы рассмотрим последнюю из самых распространённых операций с матрицами – решение системы линейных уравнений.

Напомню, что система линейных уравнений имеет вид

где A – матрица, x – вектор-столбец искомых значений, b – вектор чисел. Решение, конечно же, состоит в умножении обоих частей уравнений на матрицу,обратную A:

Этокорректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что онаобратима. Тогда xимеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.

Тутне должно возникнуть никаких сложностей, поскольку у нас уже есть весьинструментарий, необходимый для такого рода вычислений. Вы уже видели, какнаходится обратная матрица и как производить умножение матриц, а именно эти двевещи нам и нужны.

Решимпример. Aу нас будет матрицей

Этокорректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что онаобратима. Тогда xимеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.

Тутне должно возникнуть никаких сложностей, поскольку у нас уже есть весьинструментарий, необходимый для такого рода вычислений. Вы уже видели, какнаходится обратная матрица и как производить умножение матриц, а именно эти двевещи нам и нужны.

Решимпример. Aу нас будет матрицей

bу нас будет вектором [1, 2]:

b = np.array([1, 2])

Решениембудет

x = np.linalg.inv(A).dot(b)

Итак,решением являются числа 0 и 0,5. Для проверки попробуйте решить этот примервручную.

Конечно же, ввиду очень частого проведения такого рода вычислений, есть способ и получше – с помощью функции с соответствующим названием solve. Поэтому можно записать

x = np.linalg.solve(A, b)

Иполучим тот же ответ.

Если вы когда-либо прежде писали код в MATLAB, то могли заметить, что при попытке использовать метод inv MATLAB выдаёт предупреждение и сообщает, что есть и более эффективный способ вычислений. В MATLAB он называется не solve, но по сути это тот же самый алгоритм, и он действительно куда более эффективен и точен. Поэтому если у вас когда-нибудь возникнет необходимость решить подобного рода уравнение, никогда не пользуетесь inv. Всегда используйте solve.

Текстовая задача

Давайте разберём несложный пример, чтобы попрактиковаться в использовании функции solve.

Итак,поставим задачу. На небольшой ярмарке входная плата составляет 1,5 доллара для ребёнкаи 4 доллара для взрослого. Однажды за день ярмарку посетило 2200 человек; приэтом было собрано 5050 долларов входной платы. Сколько детей и сколько взрослыхпосетили ярмарку в этот день?

Итак,обозначим количество детей через X1, а количествовзрослых – через X2. Мы знаем, что

Мытакже знаем, что

Мытакже знаем, что

Обратите внимание, что это линейное уравнение, где A равно:

 а b равно :

 а b равно :

Подставимэти значения в Numpy и найдёмрешение:

A = np.array([[1,1], [1.5,4]])

b = np. array([2200, 5050])

np.linalg.solve(A, b)

Получаемответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнениевручную, чтобы проверить ответ.

Получаемответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнениевручную, чтобы проверить ответ.

python — умножение вектора матрицы numpy

Простейшее решение

Используйте numpy.dot или a.dot(b) . Смотрите документацию здесь.

 >>> a = np.array([[ 5, 1,3],
                  [ 1, 1 ,1],
                  [ 1, 2 ,1]])
>>> b = np.массив ([1, 2, 3])
>>> напечатать a.dot(b)
массив([16, 6, 8])

Это происходит потому, что массивы numpy не являются матрицами, а стандартные операции *, +, -, / работают с массивами поэлементно.

Обратите внимание, что хотя вы можете использовать numpy.matrix (по состоянию на начало 2021 года), где * будет рассматриваться как стандартное умножение матриц, numpy. matrix устарело и может быть удалено в будущих выпусках. . См. примечание в его документации (воспроизведено ниже):

Больше не рекомендуется использовать этот класс, даже для линейной алгебры. Вместо этого используйте обычные массивы. В будущем класс может быть удален.

Спасибо @HopeKing.

Другие решения

Также знайте, что есть и другие варианты:

  • Как указано ниже, при использовании python3.5+ и numpy v1.10+ оператор @ работает так, как вы ожидаете:

     >>> печать (а @ б)
массив([16, 6, 8])

  • Если вы хотите переборщить, вы можете использовать numpy.einsum . Документация даст вам представление о том, как это работает, но, честно говоря, я не совсем понимал, как его использовать, пока не прочитал этот ответ и не поиграл с ним самостоятельно.

     >>> np.einsum('ji,i->j', а, б)
массив([16, 6, 8])

  • По состоянию на середину 2016 года (numpy 1. 10.1) вы можете попробовать экспериментальный numpy.matmul , который работает как numpy.dot с двумя основными исключениями: нет скалярного умножения, но он работает со стеками матриц.

     >>> np.matmul(a, b)
массив([16, 6, 8])

  • numpy.inner работает так же, как numpy.dot для умножения матрицы на вектор, но ведет себя иначе для матрично-матричного и тензорного умножения (см. Википедию о различиях между внутренним продуктом и скалярным произведением в целом или см. этот ответ SO относительно реализаций numpy).

     >>> np.inner(a, b)
массив([16, 6, 8])
# Остерегайтесь использования для умножения матрицы на матрицу!
>>> б = а.Т
>>> нп.точка (а, б)
массив([[35, 9, 10],
       [9, 3, 4],
       [10, 4, 6]])
>>> np.inner(a, b)
массив([[29, 12, 19],
       [7, 4, 5],
       [8, 5, 6]])

  • Если у вас есть несколько 2D массивов до точка вместе, вы можете рассмотреть функцию np. linalg.multi_dot , которая упрощает синтаксис многих вложенных np.dot с. Обратите внимание, что это работает только с двумерными массивами (т.е. не для умножения матрицы на вектор).

     >>> np.dot(np.dot(a, a.T), a).dot(a.T)
  массив([[1406, 382, ​​446],
         [382, 106, 126],
         [446, 126, 152]])
  >>> np.linalg.multi_dot((а, а.Т, а, а.Т))
  массив([[1406, 382, ​​446],
         [382, 106, 126],
         [446, 126, 152]])

Более редкие варианты для крайних случаев

  • Если у вас есть тензоры (массивы размерности больше или равные единице), вы можете использовать numpy.tensordot с необязательным аргументом axes=1 :

     >>> np.tensordot(a, b, оси=1)
массив([16, 6, 8])

  • Не используйте numpy.vdot , если у вас есть матрица комплексных чисел, так как матрица будет сведена к одномерному массиву, тогда он попытается найти комплексно-сопряженное скалярное произведение между вашей сглаженной матрицей и вектором (что не удастся из-за несоответствия размера н*м против н ).

python — Как умножить два вектора и получить матрицу?

спросил

Изменено 1 год, 3 месяца назад

Просмотрено 59 тысяч раз

В операции numpy у меня есть два вектора, скажем, вектор A равен 4X1, вектор B равен 1X5, если я сделаю AXB, в результате должна получиться матрица размера 4X5.

Но я пробовал много раз, выполняя множество видов изменения формы и транспонирования, все они либо вызывают ошибку, говорящую о том, что не выровнено, либо возвращают одно значение.

Как мне получить выходной продукт матрицы, которую я хочу?

  • python
  • numpy
  • матрица
  • вектор
  • умножение матрицы

Нормальное умножение матриц работает до тех пор, пока векторы имеют правильную форму. Помните, что * в Numpy — это поэлементное умножение на 9.0026 , а умножение матриц доступно с помощью numpy.dot() (или с помощью оператора @ в Python 3.5)

 >>> numpy.dot(numpy.array([[1], [2]] ), numpy.массив([[3, 4]]))
массив([[3, 4],
       [6, 8]])

Это называется «внешний продукт». Вы можете получить его, используя простые векторы, используя numpy.outer() :

 >>> numpy.outer(numpy.array([1, 2]), numpy.array([3, 4]))
массив([[3, 4],
       [6, 8]])

Если вы используете numpy.

Во-первых, убедитесь, что у вас есть два вектора. Например, vec1.shape = (10, ) и vec2.shape = (26, ) ; в numpy вектор-строка и вектор-столбец — это одно и то же.

Во-вторых, вы делаете res_matrix = vec1.reshape(10, 1) @ vec2.reshape(1, 26) ; .

Наконец, у вас должно быть: res_matrix.shape = (10, 26) .

документация numpy говорит, что она устареет np.

No related posts.