Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Содержание

  • 1 Примеры
  • 2 Рекурсия в программировании
    • 2.1 Функции
    • 2.2 Данные
  • 3 Рекурсия в физике
  • 4 Рекурсия в лингвистике
  • 5 Цитаты
  • 6 Юмор
  • 7 См. также
  • 8 Ссылки

Примеры

  • Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
  • Факториал целого неотрицательного числа n обозначается n! и определяется как
    при n > 0 и n! = 1 при n = 0
  • Числа Фибоначчи определяются с помощью рекуррентного соотношения:
    Первое и второе числа Фибоначчи равны 1
    Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
  • Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
  • Задача «Ханойские башни». Её содержательная постановка такова:
    В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
    Рекурсивный вариант решения задачи можно описать так:

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

  • Передвиньте диск из источника в задание

В противном случае:

  • Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
  • Передвиньте оставшийся диск из источника в задание
  • Передвиньте все диски из запаса в задание используя источник как запас

Рекурсия в программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция

A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.

  • См. также Примеры реализации функции факториал

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]

Юмор

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

рекурсия 
см.
рекурсия

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

  • Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
  • Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:

«У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
«У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
…

См.

также
  • Индукция
  • Математическая индукция
  • Корекурсия
  • Рекуррентная последовательность (возвратная последовательность)

Ссылки

  1. ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?

Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.

Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.

Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).

Содержание

  • 1 Примеры
  • 2 Рекурсия в программировании
    • 2.1 Функции
    • 2.2 Данные
  • 3 Рекурсия в физике
  • 4 Рекурсия в лингвистике
  • 5 Цитаты
  • 6 Юмор
  • 7 См. также
  • 8 Ссылки

Примеры

  • Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
  • Факториал целого неотрицательного числа n обозначается n! и определяется как
    при n > 0 и n! = 1 при n = 0
  • Числа Фибоначчи определяются с помощью рекуррентного соотношения:
    Первое и второе числа Фибоначчи равны 1
    Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
  • Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
  • Задача «Ханойские башни». Её содержательная постановка такова:
    В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
    Рекурсивный вариант решения задачи можно описать так:

Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.

Если число дисков равно одному, тогда:

  • Передвиньте диск из источника в задание

В противном случае:

  • Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
  • Передвиньте оставшийся диск из источника в задание
  • Передвиньте все диски из запаса в задание используя источник как запас

Рекурсия в программировании

Функции

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.

  • См. также Примеры реализации функции факториал

Данные

Описание типа данных может содержать ссылку на саму себя.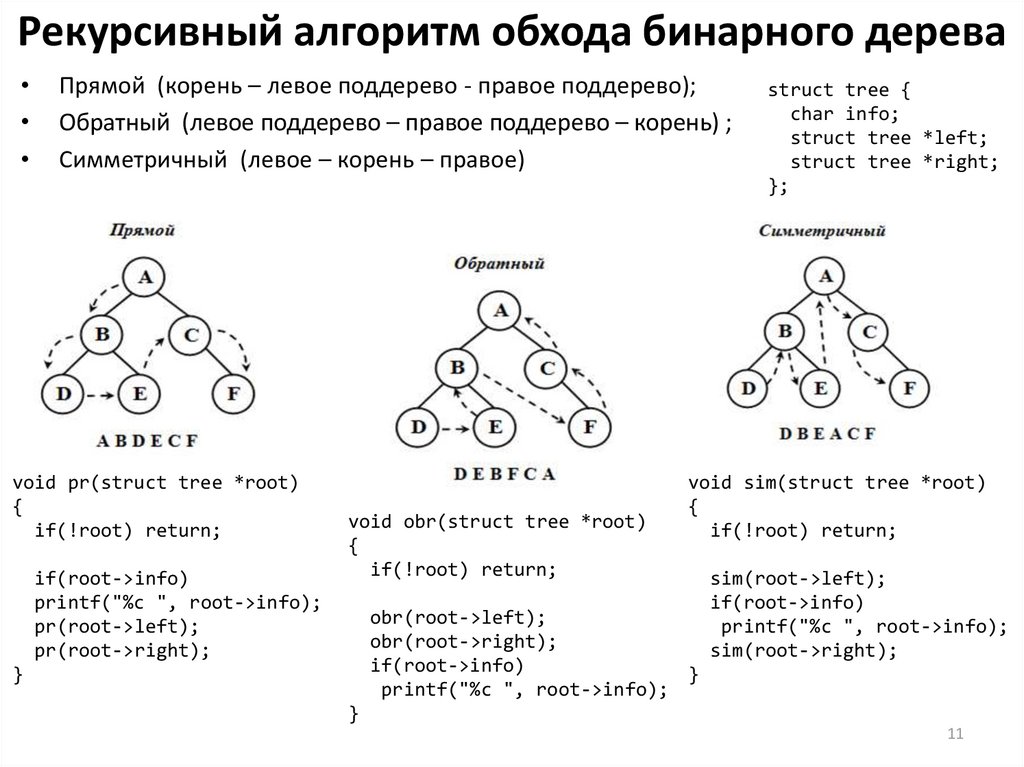 Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list
 {
   element_of_list *next; /* ссылка на следующий элемент того же типа */
   int data; /* некие данные */
 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Рекурсия в физике

Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.

Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.

Рекурсия в лингвистике

Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)

Цитаты

Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]

Юмор

Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:

рекурсия 
см. рекурсия

Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:

  • Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
  • Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).

Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:

У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:

«У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
«У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
…

См.

также
  • Индукция
  • Математическая индукция
  • Корекурсия
  • Рекуррентная последовательность (возвратная последовательность)

Ссылки

  1. ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

Рекурсивный алгоритм

Рекурсивный алгоритм

Рекурсивное определение

Предметы для изучения

  • решение задачи с помощью рекурсивного алгоритма
  • вычислительная функция с рекурсивным алгоритмом
  • Проверка принадлежности к набору с помощью рекурсивного алгоритма

Содержимое

Рекурсивный алгоритм это алгоритм, который вызывает себя с «меньшими (или более простыми)» входными значениями и получает результат для текущего ввод путем применения простых операций к возвращаемому значению для меньшего (или более простого) ввода. В более общем случае, если проблема может быть решена использование решений для небольших версии одной и той же проблемы, а меньшие версии сводятся к легко решаемым случаям, тогда можно использовать рекурсивный алгоритм для решения этой проблемы. Например, элементы рекурсивно определенного множества или значение рекурсивно определенной функции. можно получить рекурсивным алгоритмом.

Если набор или функция определены рекурсивно, то рекурсивный алгоритм вычисления его члены или значения отражают определение. Начальные шаги рекурсивного алгоритма соответствуют базовому предложению рекурсивного определения и идентифицируют базовые элементы. Затем за ними следуют шаги, соответствующие индуктивному предложению, которые сокращают вычисление элемента одного поколения к поколению элементы непосредственно предшествующего поколения.

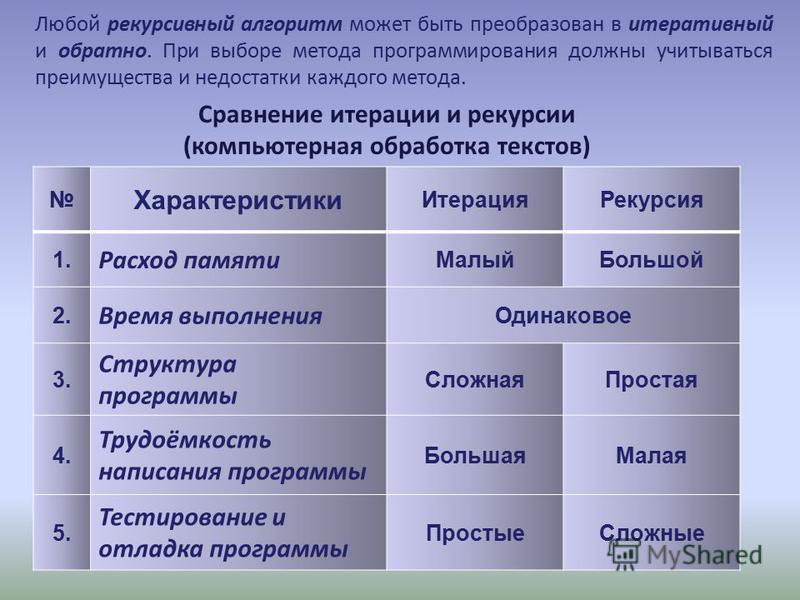
В общем, рекурсивные компьютерные программы требуют больше памяти и вычислений по сравнению с итеративными алгоритмы, но они проще и во многих случаях являются естественным способом осмысления проблемы.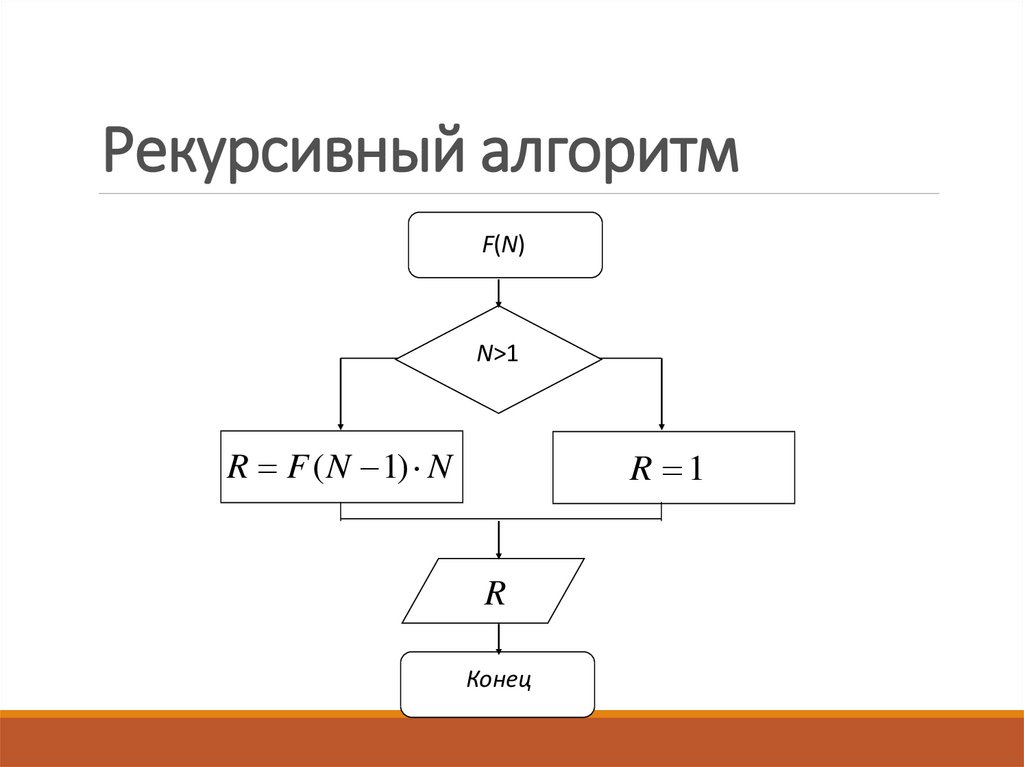

Пример 1: Алгоритм нахождения k -го четного натурального числа
Обратите внимание, что это можно очень легко решить, просто выведя 2 *( k — 1 ) для данного к . Однако цель здесь — проиллюстрировать основную идею рекурсии, а не решить проблему.

Алгоритм 1:  Четное ( положительное целое число k )
Вход: k , положительное целое число
Вывод: k -е четное натуральное число (первое четное 0 )

Алгоритм:
если к = 1 , то вернуть 0 ;
иначе возврат Четный( k-1 ) + 2 .

Здесь вычисление Even( k ) сводится к вычислению Четный для меньшего входного значения, т.е. Четный( к-1 ). Четное( k ) в итоге становится Четное( 1 ) это 0 по первой строке. Например, для вычисления Even( 3 ) , Алгоритм Even( k ) вызывается с к = 2 . При вычислении Четный( 2 ) , Алгоритм Even( k ) вызывается с помощью k = 1 . Поскольку Even( 1 ) = 0, 0 возвращается для вычисления Чет( 2 ) и Чет( 2 ) = Чет( 1 ) + 2 = 2 есть полученный. Это значение 2 для Четный( 2 ) теперь возвращается для вычисления Четный( 3 ) и Чет ( 3 ) = Чет ( 2 ) + 2 = 4 получается.
Как видно из сравнения этого алгоритма с рекурсивным определением набор неотрицательных четных чисел первая строка алгоритма соответствует основному пункту определения, а вторая строка соответствует к индуктивному предложению.

Для сравнения посмотрим, как та же задача может быть решена с помощью итеративного алгоритма.

Алгоритм 1-a:  Четное ( положительное целое число k )
Ввод: k , положительное целое число
Вывод: k -е четное натуральное число (первое четное 0 )

Алгоритм:
int i , даже ;
i := 1 ;
даже := 0 ;
в то время как ( я < к ) {
          четный := четный + 2 ;
          i := i + 1 ;
}
вернуть даже .

Пример 2: Алгоритм вычисления k -й степени 2

Алгоритм 2  степень_2( натуральное число к)
Ввод: k , натуральное число
Выход: k -я степень числа 2

Алгоритм:
если к = 0 , то вернуть 1 ;
иначе вернуть 2*степень_2(k — 1 ) .

Для сравнения посмотрим, как та же задача может быть решена с помощью итеративного алгоритма.

Алгоритм 2-a  степень_2( натуральное число k)
Ввод: k , натуральное число
Выход: k -я степень числа 2

Алгоритм:
int i , мощность ;
i := 0 ;
мощность := 1 ;
пока( i < k ) {
          мощность := мощность * 2 ;
          i := i + 1 ;
}
возврат мощность .

Следующий пример не имеет соответствующего рекурсивного определения. Он показывает рекурсивный способ решения проблемы.

Пример 3: Рекурсивный алгоритм последовательного поиска

Алгоритм 3  SeqSearch( L, i, j, x )

Ввод: L — массив, i и j — положительные целые числа, i j и x ключ искать в L .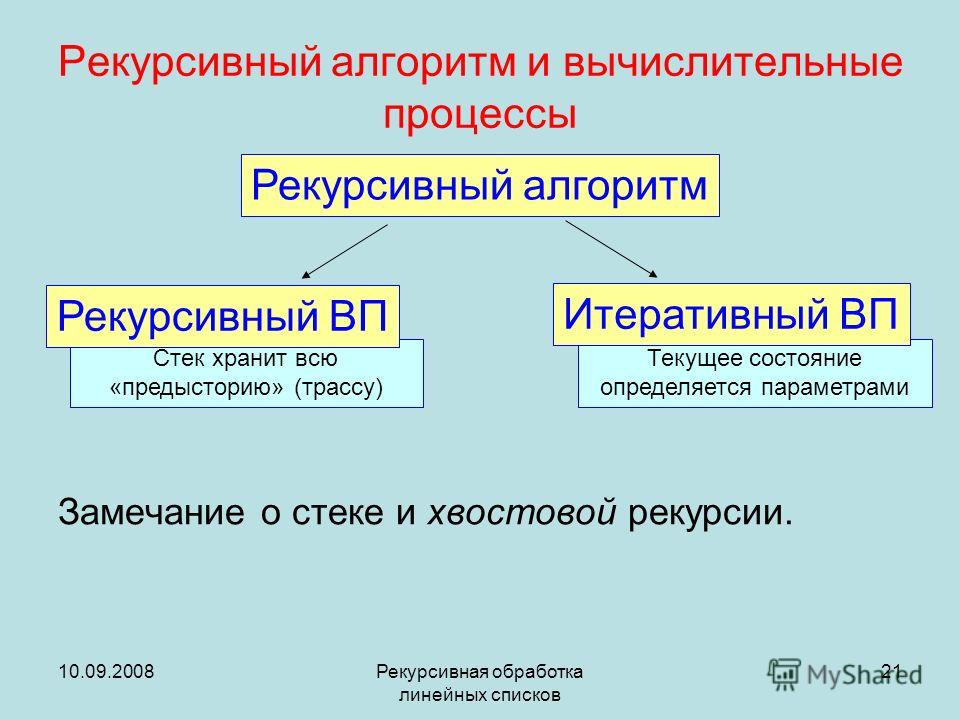
Вывод: Если x находится в L между индексами и и j , затем выведите его индекс, иначе выведите 0 .

Алгоритм:
если я j , затем
{
    , если L ( i ) = x , , затем возврат и ;
    иначе вернуть SeqSearch( л, я+1, у, х )
}
иначе вернуть 0 .

Рекурсивные алгоритмы также можно использовать для проверки объектов на принадлежность к множеству.

Пример 4: Алгоритм проверки того, является ли число натуральным x

Алгоритм 4  Естественный( число x )
Ввод: Число x
Вывод: » Да » если x является натуральным числом, иначе » Нет »

Алгоритм:
если x < 0 ,   тогда вернуть « Нет »
еще
    если x = 0 ,   , то вернуть « Да »
    иначе возврат Натуральный( x — 1 )

Пример 5: Алгоритм проверки того, является ли выражение w предложением (форма предложения)

Алгоритм 5 Предложение ( строка w )

Вход: Строка А w
Вывод: » Да » если w является предложением, иначе » Нет »

Алгоритм:
если w равно 1 (истина), 0 (ложь), или пропозициональная переменная, , затем , возврат « Да »
иначе если w = ~ w 1 , затем возврат Предложение ( с 1 )
   иначе
     если ( w = w 1 с 2 или с 1 с 2 или с 1 с 2 или с 1 с 2 ) и
Предложение ( w 1 ) = Да и  Предложение ( w 2 ) = Да
     затем возврат Да
     иначе вернуть Нет
конец

Проверьте свое понимание рекурсивного алгоритма

Укажите, какие из следующих утверждений верны, а какие нет.
Нажмите «Да» или «Нет» , затем «Отправить».

Далее — Первый принцип математической индукции

Вернуться к расписанию
Вернуться к оглавлению

Рекурсия функций Python

❮ Глоссарий Python

Рекурсия

Python также допускает рекурсию функций, что означает, что определенная функция может вызывать сама себя.

Рекурсия — это общая концепция математики и программирования. Это означает, что функция вызывает сама себя. Преимущество этого заключается в том, что вы можете перебирать данные для достижения результата.

Разработчик должен быть очень осторожен с рекурсией, поскольку может быть очень легко написать функцию, которая никогда не завершится, или функцию, которая использует избыточное количество памяти или мощности процессора. Однако при правильном написании рекурсия может быть очень эффективным и математически элегантным подходом к программированию.

В этом примере tri_recursion() — это функция, которую мы определили для вызова самой себя («recurse»). Мы используем переменную k в качестве данных, которые уменьшаются (-1) каждый раз, когда мы рекурсивно. Рекурсия заканчивается, когда условие не больше 0 (т. е. когда оно равно 0).

Новому разработчику может потребоваться некоторое время, чтобы понять, как именно это работает, лучший способ выяснить это — протестировать и изменить его.

Пример

Пример рекурсии

защита tri_recursion(k):
если(к>0):
результат = k+tri_recursion(k-1)
печать (результат)
еще:
результат = 0
return result

print(«\n\nРезультаты примера рекурсии»)
tri_recursion(6)

Попробуйте сами »

Связанные страницы

Учебное пособие по функциям Python Функция Вызов функции Аргументы функции *аргументы Аргументы ключевых слов **кваргс Значение параметра по умолчанию Передача списка в качестве аргумента Возвращаемое значение функции Оператор pass i Функции

❮ Глоссарий Python


ПИКЕР ЦВЕТА

Лучшие учебники
Учебник по HTML
Учебник по CSS
Учебник по JavaScript
Учебник How To
Учебник по SQL
Учебник по Python
Учебник по W3.

No related posts.