Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?
Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.
Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.
Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).
Содержание
|
Примеры
- Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.

- Факториал целого неотрицательного числа n обозначается n! и определяется как
- при n > 0 и n! = 1 при n = 0
- Числа Фибоначчи определяются с помощью рекуррентного соотношения:
- Первое и второе числа Фибоначчи равны 1
- Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
- Практически все геометрические фракталы задаются в форме бесконечной рекурсии. (например, треугольник Серпинского).
- Задача «Ханойские башни». Её содержательная постановка такова:
- В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера.
 При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света. - Рекурсивный вариант решения задачи можно описать так:
- В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера.
Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.
Если число дисков равно одному, тогда:
- Передвиньте диск из источника в задание
В противном случае:
- Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
- Передвиньте оставшийся диск из источника в задание
- Передвиньте все диски из запаса в задание используя источник как запас
Рекурсия в программировании
Функции
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция
 Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.
Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.
- См. также Примеры реализации функции факториал
Данные
Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
class element_of_list
{
element_of_list *next; /* ссылка на следующий элемент того же типа */
int data; /* некие данные */
};
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.
Рекурсия в физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
Рекурсия в лингвистике
Способность языка порождать вложенные предложения и конструкции. Базовое предложение
 Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)Цитаты
Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]
Юмор
Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см.
рекурсия
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
- Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- …
См.
 также
также- Индукция
- Математическая индукция
- Корекурсия
- Рекуррентная последовательность (возвратная последовательность)
Ссылки
- ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?
Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.
Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.
Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).
Содержание
|
Примеры
- Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
- Факториал целого неотрицательного числа n обозначается n! и определяется как
- при n > 0 и n! = 1 при n = 0
- Числа Фибоначчи определяются с помощью рекуррентного соотношения:
- Первое и второе числа Фибоначчи равны 1
- Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
- Практически все геометрические фракталы задаются в форме бесконечной рекурсии.
 (например, треугольник Серпинского).
(например, треугольник Серпинского). - Задача «Ханойские башни». Её содержательная постановка такова:
- В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
- Рекурсивный вариант решения задачи можно описать так:
Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.
Если число дисков равно одному, тогда:
- Передвиньте диск из источника в задание
В противном случае:
- Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
- Передвиньте оставшийся диск из источника в задание
- Передвиньте все диски из запаса в задание используя источник как запас
Рекурсия в программировании
Функции
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.
Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.
- См. также Примеры реализации функции факториал
Данные
Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
class element_of_list
{
element_of_list *next; /* ссылка на следующий элемент того же типа */
int data; /* некие данные */
};
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.
Рекурсия в физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
Рекурсия в лингвистике
Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Цитаты
Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]
Юмор
Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см.
рекурсия
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
- Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- …
См.
 также
также- Индукция
- Математическая индукция
- Корекурсия
- Рекуррентная последовательность (возвратная последовательность)
Ссылки
- ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?
Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.
Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.
Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).
Содержание
|
Примеры
- Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
- Факториал целого неотрицательного числа n обозначается n! и определяется как
- при n > 0 и n! = 1 при n = 0
- Числа Фибоначчи определяются с помощью рекуррентного соотношения:
- Первое и второе числа Фибоначчи равны 1
- Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
- Практически все геометрические фракталы задаются в форме бесконечной рекурсии.
 (например, треугольник Серпинского).
(например, треугольник Серпинского). - Задача «Ханойские башни». Её содержательная постановка такова:
- В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
- Рекурсивный вариант решения задачи можно описать так:
Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.
Если число дисков равно одному, тогда:
- Передвиньте диск из источника в задание
В противном случае:
- Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
- Передвиньте оставшийся диск из источника в задание
- Передвиньте все диски из запаса в задание используя источник как запас
Рекурсия в программировании
Функции
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.
Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.
- См. также Примеры реализации функции факториал
Данные
Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
class element_of_list
{
element_of_list *next; /* ссылка на следующий элемент того же типа */
int data; /* некие данные */
};
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.
Рекурсия в физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
Рекурсия в лингвистике
Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Цитаты
Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]
Юмор
Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см.
рекурсия
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
- Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- …
См.
 также
также- Индукция
- Математическая индукция
- Корекурсия
- Рекуррентная последовательность (возвратная последовательность)
Ссылки
- ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Рекурсивный алгоритм | это… Что такое Рекурсивный алгоритм?
Реку́рсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса, ссылающегося прямо или косвенно на эти базовые случаи.
Другими словами, рекурсия — способ общего определения объекта или действия через себя, с использованием ранее заданных частных определений. Рекурсия используется, когда можно выделить самоподобие задачи.
Определение в логике, использующее рекурсию, называется индуктивным (см., например, Натуральное число).
Содержание
|
Примеры
- Метод Гаусса — Жордана для решения Системы линейных алгебраических уравнений является рекурсивным.
- Факториал целого неотрицательного числа n обозначается n! и определяется как
- при n > 0 и n! = 1 при n = 0
- Числа Фибоначчи определяются с помощью рекуррентного соотношения:
- Первое и второе числа Фибоначчи равны 1
- Для n > 2, n − e число Фибоначчи равно сумме (n − 1)-го и (n − 2)-го чисел Фибоначчи
- Практически все геометрические фракталы задаются в форме бесконечной рекурсии.
 (например, треугольник Серпинского).
(например, треугольник Серпинского). - Задача «Ханойские башни». Её содержательная постановка такова:
- В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
- Рекурсивный вариант решения задачи можно описать так:
Алгоритм по передвижению башни, алгоритм передвинет нужное количество дисков из пирамиды «источник» на пирамиду «задание» используя «запасную» пирамиду.
Если число дисков равно одному, тогда:
- Передвиньте диск из источника в задание
В противном случае:
- Рекурсивно передвиньте все диски кроме одного из источника в запас, используя задание как запас
- Передвиньте оставшийся диск из источника в задание
- Передвиньте все диски из запаса в задание используя источник как запас
Рекурсия в программировании
Функции
В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.
Мощь рекурсивного определения объекта в том, что такое конечное определение способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.
Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за этот счёт работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что рекурсивные вызовы не бесплатны — на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.
Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивают выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. К сожалению, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Lisp), описание которого содержит все необходимые сведения.
- См. также Примеры реализации функции факториал
Данные
Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
Подобные структуры используются при описании списков и графов. Пример описания списка (C++):
class element_of_list
{
element_of_list *next; /* ссылка на следующий элемент того же типа */
int data; /* некие данные */
};
Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.
Рекурсия в физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Другим примером бесконечной рекурсии является эффект самовозбуждения (положительной обратной связи) у электронных схем усиления, когда сигнал с выхода попадает на вход, усиливается, снова попадает на вход схемы и снова усиливается. Усилители, для которых такой режим работы является штатным, называются автогенераторы.
Рекурсия в лингвистике
Способность языка порождать вложенные предложения и конструкции. Базовое предложение кошка съела мышь может быть за счет рекурсии расширено как Ваня догадался, что кошка съела мышь, далее как Катя знает, что Ваня догадался, что кошка съела мышь и так далее. Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Рекурсия считается одной из лингвистических универсалий, то есть свойственна любому естественному языку (хотя в последнее время активно обсуждается возможное отсутствие рекурсии в одном из языков Амазонии — пираха, которое отмечает лингвист Д. Эверетт). О рекурсии в лингвистике, ее разновидностях и наиболее характерных проявлениях в русском языке описано в статье Е.А.Лодатко «Рекурсивные лингвистические структуры» (см.: Рекурсивные лингвистические структуры)
Цитаты
Итерация от человека. Рекурсия — от Бога. — Л. Питер Дойч[1]
Юмор
Большая часть всех шуток о рекурсии касается бесконечной рекурсии, в которой нет условия выхода. Известные высказывания: ‘Чтобы понять рекурсию, нужно сначала понять рекурсию’, ‘Чтобы что-то сделать, надо что-то сделать’, ‘Для приготовления салата необходимы: огурцы, помидоры, салат’. Весьма популярна шутка о рекурсии, напоминающая словарную статью:
- рекурсия
- см.
рекурсия
Несколько рассказов Станислава Лема посвящены (возможным) казусам при бесконечной рекурсии:
- Рассказ про Йона Тихого «Путешествие четырнадцатое» из «Звёздных дневников Ийона Тихого», в котором герой последовательно переходит от статьи о сепульках к статье о сепуляции, оттуда к статье о сепулькариях, в которой снова стоит отсылка к статье «сепульки».
- Рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
Русская народная сказка-песня «У попа была собака…» являет пример рекурсии:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- «У попа была собака, он её любил,
- Она съела кусок мяса, он её убил,
- В землю закопал,
- Надпись написал:
- …
См.
 также
также- Индукция
- Математическая индукция
- Корекурсия
- Рекуррентная последовательность (возвратная последовательность)
Ссылки
- ↑ * Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1
Рекурсивные алгоритмы
Определение 1
Рекурсивные алгоритмы — это алгоритмы, которые решают поставленные задачи с помощью приведения их к разрешению одной или более аналогичных задач, но в более коротком их представлении.
Рекурсивные алгоритмы
Под рекурсией понимается способ представления типа объектов или методов путём предварительного задания одного или больше (как правило упрощённых) его основных случаев или методик, а далее представлением на их базе правил формирования рассматриваемого типа, которые непосредственно или опосредовано ссылаются на эти основные случаи.
Замечание 1
По-иному, рекурсия — это метод обобщённого представления объекта или воздействия через самого себя, с применением задаваемых раньше конкретных определений.
Рекурсию возможно применять, когда есть возможность выделения подобной самой себе задачи. В качестве примера можно привести задачу «Ханойские башни». Она содержит следующую постановку задачи. Монахи одного из буддийских монастырей перекладывают кольца в течение примерно уже тысячи лет. У них есть три пирамиды, на которые одеты кольца различных размерных величин. Изначально шестьдесят четыре кольца располагались надетыми на первую из пирамид в порядке убывания их размеров. Задачей монахов было перекладывание всех колец с исходной пирамиды на следующую, при соблюдении одного условия, перекладываемое кольцо не допускается класть на кольцо, размеры которого меньше. При операции перемещения колец допускается использование всех трёх пирамид. Скорость перекладывания колец монахами составляет одно кольцо в секунду. Когда они завершат свою задачу, придёт конец света. В рекурсивном варианте решение задачи будет выглядеть следующим образом. Алгоритм перемещения башни переместит необходимое число колец из пирамиды «источника» на пирамиду «приёмник» применяя «запас» в виде третьей пирамиды. При количестве колец равном одному, алгоритм будет следующим: переместите кольцо из источника в приёмник. Конец.
Когда они завершат свою задачу, придёт конец света. В рекурсивном варианте решение задачи будет выглядеть следующим образом. Алгоритм перемещения башни переместит необходимое число колец из пирамиды «источника» на пирамиду «приёмник» применяя «запас» в виде третьей пирамиды. При количестве колец равном одному, алгоритм будет следующим: переместите кольцо из источника в приёмник. Конец.
Если число колец больше:
- Используя рекурсию переместите все кольца, за исключением одного, из источника в запас, применяя приёмник в качестве запаса.
- Переместите последнее кольцо из источника в приёмник.
- Переместите все кольца из запаса в приёмник, применяя источник в качестве запаса.
Рекурсивные алгоритмы в программировании
Определение 2
Рекурсия в программировании — это обращение к процедуре (функции) напрямую из самой программы (простая рекурсия) или же с использованием других функций (сложная рекурсия).
К примеру программная функция А обращается к функции В, а функция В обращается к функции А. Число вложенных обращений к функциям или процедурам следует называть глубиной рекурсии.
Число вложенных обращений к функциям или процедурам следует называть глубиной рекурсии.
Замечание 2
Сильная сторона рекурсивного задания объекта состоит в том, что такая законченная формулировка способна описать бесконечное количество объектов. При помощи рекурсивных программ есть возможность описывать бесконечные вычислительные операции, при этом, не допуская явного повторения части программ.
Организация рекурсивных обращений в языках и операционных средах программирования, используемых на практике, почти всегда основано на механизме стека обращений. Адреса возврата и текущие переменные операции сохраняются в стеке, что позволяет каждому последующему рекурсивному обращению к этой функции использовать свой комплект текущих переменных и поэтому всё работает правильно. Но с другой стороны этот простой по организации механизм требует затрачивать на каждое обращение определённый массив оперативной памяти компьютера, что при значительной глубине рекурсии способно вызвать переполнение стека обращений. По этой причине не следует злоупотреблять использованием программ с рекурсией, которые способны привести к чрезмерно глубокой рекурсии.
По этой причине не следует злоупотреблять использованием программ с рекурсией, которые способны привести к чрезмерно глубокой рекурсии.
Но следует заметить, что существует особый рекурсивный тип, обозначаемый как «хвостовая рекурсия». Специальные средства программных языков (компиляторы и интерпретаторы), которые поддерживают выработку оптимального кода (исходного или который исполняется), в автоматическом режиме выполняют преобразование хвостовой рекурсии в итерацию. Это позволяет обеспечить функционирование алгоритмов с хвостовыми рекурсиями в небольшом пространстве оперативной памяти. В этом случае даже практически бесконечные рекурсивные вычисления (к примеру, если рекурсией выполняется функционирование интерпретатора команд, воспринимающего пользовательские команды), не могут привести к переполнению памяти.
Но надо также отметить, что не во всех языках программирования есть правила, которые жёстко регламентируют условия работы рекурсивных операций, позволяющие в любом случае преобразовать их в итерацию. Исключением является язык Lisp, который обладает всеми необходимыми свойствами.
Исключением является язык Lisp, который обладает всеми необходимыми свойствами.
Рекурсивные алгоритмы в других областях
Рекурсия в физических процессах. Наглядным примером бесконечного рекурсивного алгоритма могут служить два зеркала, установленные напротив друг друга. В каждом зеркале образованы коридоры из повторяющихся отражений другого зеркала. Ещё одним вариантом бесконечного рекурсивного алгоритма выступает самовозбуждение при положительной обратной связи в усилителе электрических сигналов, то есть в случае проникновения выходного сигнала на вход усилителя. На этом принципе построены схемы генераторов, для которых режим самовозбуждения является штатным.
Рекурсивные алгоритмы присутствуют также в области лингвистики. Это, например, могут быть языковые возможности создавать вложенные конструкции и предложения. Например, исходное предложение «кошка поймала мышь» можно расширить, применяя рекурсивный алгоритм, до «Вася понял, что кошка поймала мышь». Затем «Лиза узнала, что Вася понял, что кошка поймала мышь» и так можно продолжать бесконечно. Рекурсивный алгоритм можно считать универсальным лингвистическим методом, который есть в любом естественном языке. Но существует мнение, что в некоторых языках Амазонии свойство рекурсии не заложено изначально.
Рекурсивный алгоритм можно считать универсальным лингвистическим методом, который есть в любом естественном языке. Но существует мнение, что в некоторых языках Амазонии свойство рекурсии не заложено изначально.
Рекурсия – жемчужина теории алгоритмов — Scratch
ВИКТОР КОХОВЕЦ
учитель информатики и математики Валищенской средней школы Пинского района
В информатике в понятие «рекурсия» вкладывается следующий смысл: это прием программирования, при котором подпрограмма вызывает саму себя либо непосредственно, либо косвенно.
Звучит просто, но, как только мы начинаем знакомиться с ней или знакомить наших наиболее способных учеников, появляется много вопросов и проблем: что, зачем и как это вообще работает?
Зачем это нужно?
Так зачем же нужна рекурсия? Нельзя ли обойтись без нее? Есть ли у нее преимущества в сравнении с более простыми и доступными для понимания приемами?
В теории алгоритмов есть теорема, которая говорит о том, что рекурсия и итерация эквивалентны. Это значит, что любой алгоритм, который можно реализовать рекурсивно, с таким же успехом может быть реализован и итеративно, и наоборот. Может, действительно, не стоит тратить на нее время и силы, а использовать только циклы?
Это значит, что любой алгоритм, который можно реализовать рекурсивно, с таким же успехом может быть реализован и итеративно, и наоборот. Может, действительно, не стоит тратить на нее время и силы, а использовать только циклы?
Здесь необходимо понимать то, что теория и практика не всегда совпадают. То, что любую рекурсию можно заменить итерацией, совсем не значит, что этот итерационный код будет компактным, понятным и быстро работающим. Существует огромное количество задач, для которых именно рекурсивное решение является оптимальным. Например, алгоритмы быстрой сортировки, работы с деревьями, построения фракталов, обхода графов и многие другие. Именно в них рекурсия показывает свою мощь, опережая любые другие реализации по скорости работы и компактности кода.
Но применение рекурсии не всегда оправданно. Есть очень много примеров, в которых применение рекурсии просто расточительно и не выдерживает никакой конкуренции с итерацией. К таким примерам можно отнести и задачи, на которых обычно и объясняют работу рекурсивных алгоритмов: нахождение факториала числа и вычисление чисел ряда Фибоначчи.
Обычно задачи, в которых использование рекурсии имеет смысл, являются далеко не тривиальными. В них часто необходимо использовать такой прием, как разбиение задачи на простые шаги, каждый из которых тоже можно разложить на более мелкие шаги и так далее, пока не доберемся до самых элементарных «шажочков». Такие задачи не по силам большинству учащихся, и знакомство с рекурсией, как мне кажется, является целесообразным только на занятиях с высокомотивированными детьми, при подготовке к олимпиадам и конкурсам по информатике.
Но на самом деле рекурсия – это тонкий и изящный инструмент, который при умелом использовании способен сослужить добрую службу. Задача программиста – не только овладеть обоими подходами, но и научиться выбирать, какой из них применить в том или ином конкретном случае.
Как это работает?
Scratch дает замечательную возможность легко изучить основные алгоритмические структуры: следование, ветвление, циклы и подпрограммы. Легкость обусловлена наглядностью кода и отсутствием языковых проблем.
Легкость обусловлена наглядностью кода и отсутствием языковых проблем.
Уже начиная с версии 2.0 в Scratch появилась возможность использовать рекурсивный вызов блока «Другие блоки». Давайте посмотрим, как с его помощью можно легко разобраться в принципах организации и работы рекурсивных алгоритмов.
Иногда для того, чтобы понять, как необходимо действовать правильно, стоит рассмотреть противоположный случай и сделать неправильно. Сейчас мы поступим именно так. Рассмотрим элементарный алгоритм, в котором реализован рекурсивный вызов: «Пример неправильного рекурсивного алгоритма» .
Несомненно, что этот алгоритм является рекурсивным, так как в подпрограмме «Следующий шаг» есть вызов ее же самой. Запустив скрипт, мы увидим, что кот бесконечно «ходит» по сторонам квадрата и, когда он делает следующий шаг, переменная «Глубина рекурсии» увеличивается на единицу.
Самое интересное начнется, если мы включим Турборежим (Редактировать / Включить Турборежим) и откроем вкладку Процессы в Диспетчере задач Windows (Ctrl+Alt+Del / Диспетчер задач / Подробнее). Там мы сможем увидеть, что с каждой секундой объем памяти, занимаемый браузером, возрастает. Если не прервать выполнение программы, то ресурсы системы будут исчерпаны и работа завершится аварийно. У меня на глубине рекурсии около 10 миллионов вкладка с проектом стала занимать больше 2 Гб оперативной памяти, а затем прекратила работу:
Там мы сможем увидеть, что с каждой секундой объем памяти, занимаемый браузером, возрастает. Если не прервать выполнение программы, то ресурсы системы будут исчерпаны и работа завершится аварийно. У меня на глубине рекурсии около 10 миллионов вкладка с проектом стала занимать больше 2 Гб оперативной памяти, а затем прекратила работу:
Этот пример показывает, что каждый вызов рекурсии занимает дополнительную память на хранение стека вызовов, хотя и расходует ее довольно экономно. Безусловно, в таком виде использовать рекурсию нельзя!
Правильный рекурсивный алгоритм должен содержать в себе условие, которое проверяется перед рекурсивным вызовом. В рекурсивной подпрограмме всегда должны быть два случая: рекурсивный и граничный. Рекурсивный случай – когда подпрограмма вызывает саму себя, а граничный – когда подпрограмма перестает себя вызывать. Наличие граничного случая и предотвращает бесконечную работу алгоритма.
Фрактальное дерево
Давайте рассмотрим, как это работает, на примере алгоритма рисования фрактального дерева.
Мы будем двигаться от простого к сложному и начнем с рисования простейшей части дерева – ветки. Создадим новую подпрограмму с помощью блока «Другие блоки». Назовем ее «Дерево1» и будем передавать в нее длину рисуемой ветки. Никакой рекурсии – опускаем перо и делаем 50 шагов вперед и столько же назад.
Следующий уровень – блок «Дерево2». В любом дереве есть развилки, поэтому и мы нарисуем развилку. Рисуем прямую линию и отходящие от нее два дерева первого уровня (с помощью предыдущей подпрограммы) меньшего размера, а затем возвращаемся в первоначальную точку. Никакой магии, никакой рекурсии.
Движемся дальше – блок «Дерево3». На третьем уровне снова рисуем прямую линию и отходящие от нее два дерева, но уже не первого, а второго уровня, опять же используя уже созданные подпрограммы. Снова никакой рекурсии, все обычно и просто, но мы уже начинаем видеть дерево.
Понятно, что этот процесс можно продолжить и создать подпрограммы «Дерево4», «Дерево5», «Дерево6» и так далее, получая с каждым шагом все более интересные рисунки.
Но зачем делать много новых скриптов? Легко можно заметить, что «Дерево2» и «Дерево3» отличаются друг от друга только цифрами в названиях процедур. Давайте добавим в определение блока еще один параметр – «Уровень» – и при вызове блока «Дерево» будем уменьшать его на единицу. Также необходимо заметить, что блок «Дерево1» не вызывал никаких других блоков, поэтому этот случай в новом блоке рассмотрен отдельно.
Это уже рекурсивный алгоритм. Причем он организован правильно и содержит в себе и граничный случай (когда переменная Уровень равна 1), и рекурсивный (ветка «Иначе»).
Немного доработаем его – добавим возможность изменять числа, которые используются в нем, а также добавим случайный фактор, который будет влиять на эти числа. Результат доступен по адресу . На большой глубине рекурсии необходимо выполнять в Турборежиме.
Как видно из этого примера, довольно простой рекурсивный алгоритм позволяет строить сложные фрактальные деревья.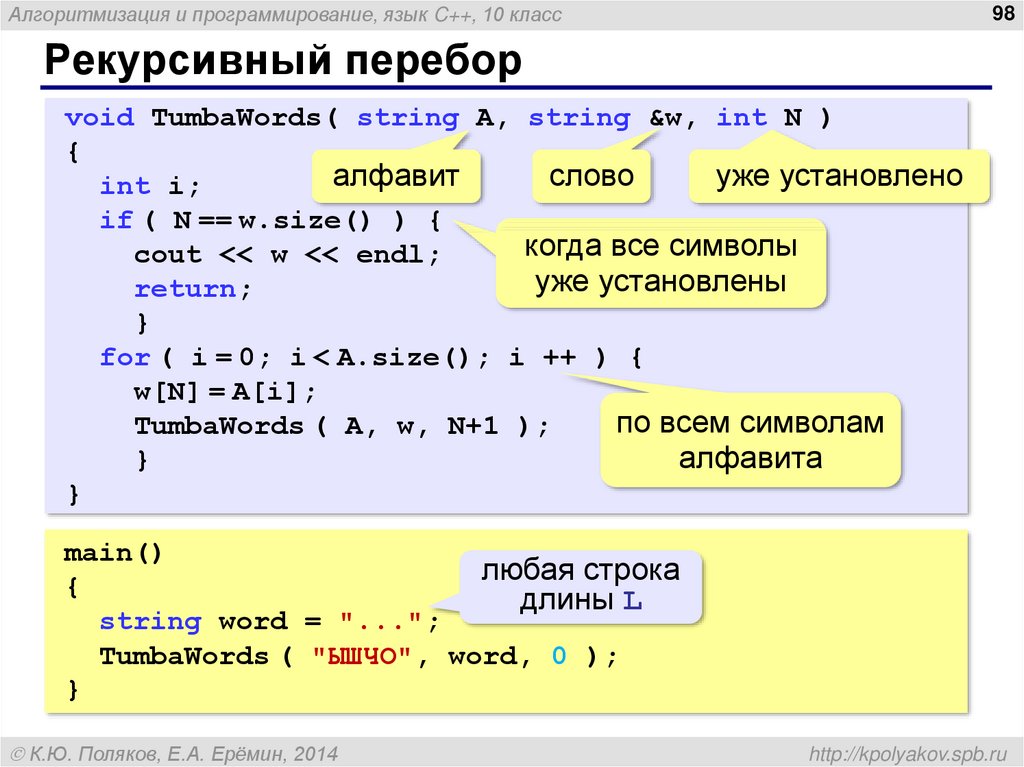 Итерационная реализация будет гораздо сложнее.
Итерационная реализация будет гораздо сложнее.
Задача о ханойских башнях
Рассмотрим еще один интересный рекурсивный алгоритм. Его можно встретить во многих книгах по программированию, но в Scratch его еще не рассматривали. Речь идет о задаче о ханойских башнях.
В одной из древних легенд говорится следующее. «В храме Бенареса находится бронзовая плита с тремя алмазными стержнями. На один из стержней Бог при сотворении мира нанизал 64 диска разного диаметра из чистого золота так, что наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя законам Брамы:
1. Диски можно перемещать с одного стержня на другой только по одному;
2. Нельзя класть больший диск на меньший.
Когда все 64 диска будут перенесены с одного стержня на другой, и башня, и храмы, и жрецы-брамины превратятся в прах, и наступит конец света».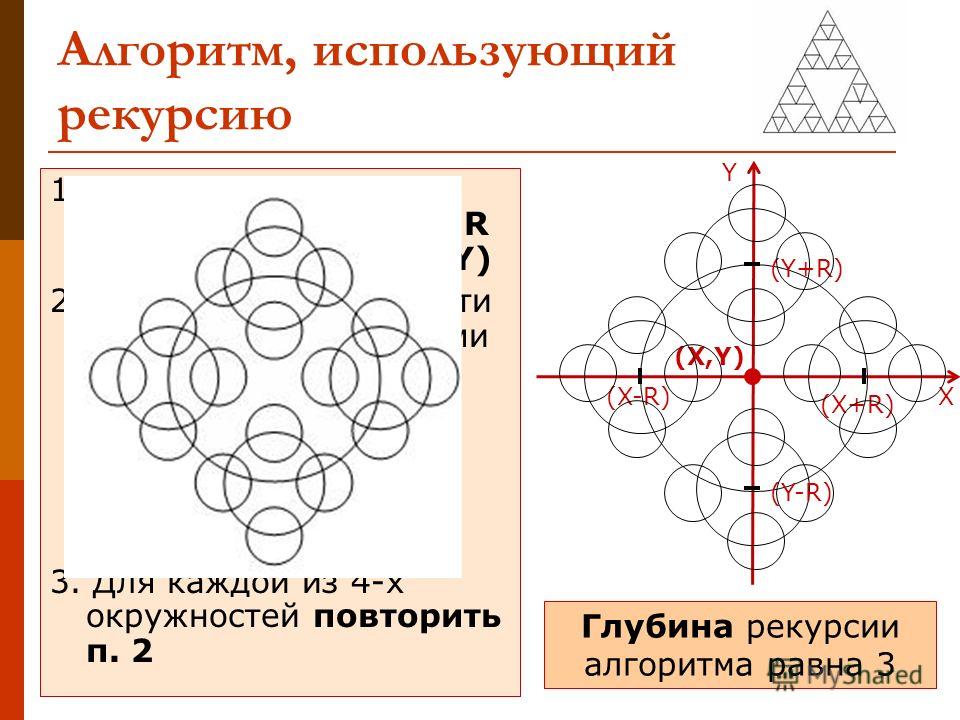
Эта древняя легенда породила задачу о ханойских башнях: переместить m дисков с одного из трех стержней на другой, соблюдая «законы Брамы».
Пронумеруем стержни слева направо от 1 до 3. Задача состоит в переносе m дисков с левого стержня на правый.
Задача может быть решена одним перемещением только для одного (m = 1) диска. В общем случае потребуется минимум перемещение.
Построим математическое рекурсивное решение задачи, состоящее из трех этапов:
1. Перенести башню, состоящую из m – 1 диска, со стержня № 1 на стержень № 2;
2. Перенести один оставшийся диск со стержня № 1 на стержень № 3;
3. Перенести башню, состоящую из m – 1 диска, со стержня № 2 на стержень № 3.
Таким образом, задача о перемещении m дисков сводится к задаче о перемещении m – 1 диска. Обращаясь опять к этому же алгоритму, сведем задачу к перемещению m – 2 дисков. Продолжая этот процесс, получим в конце концов задачу о перемещении одного диска. Эта задача решается за один ход. Таким образом, в процессе решения возникают промежуточные задачи: переместить башню из нескольких n дисков с одного стержня на другой.
Продолжая этот процесс, получим в конце концов задачу о перемещении одного диска. Эта задача решается за один ход. Таким образом, в процессе решения возникают промежуточные задачи: переместить башню из нескольких n дисков с одного стержня на другой.
Обозначим тот стержень, с которого следует снять диски, через i1, а тот, на который надеть, через i2. Тогда номер вспомогательного стержня равен 6 – i1 – i2.
Оформим алгоритм решения задачи о переносе башни из n дисков с i1 на i2 в виде нового блока с тремя параметрами: n, i1, i2:
Решение задачи о ханойских башнях доступно на сайте Scratch по ссылке https://scratch.mit.edu/projects/190497395/.
Помимо текстового решения там размещены анимированные реализации, которые представляют собой игры-головоломки. Они позволяют попробовать решить задачу самому, а затем сравнить свое решение с решением компьютера: https://scratch.mit.edu/projects/217088119/
и https://scratch.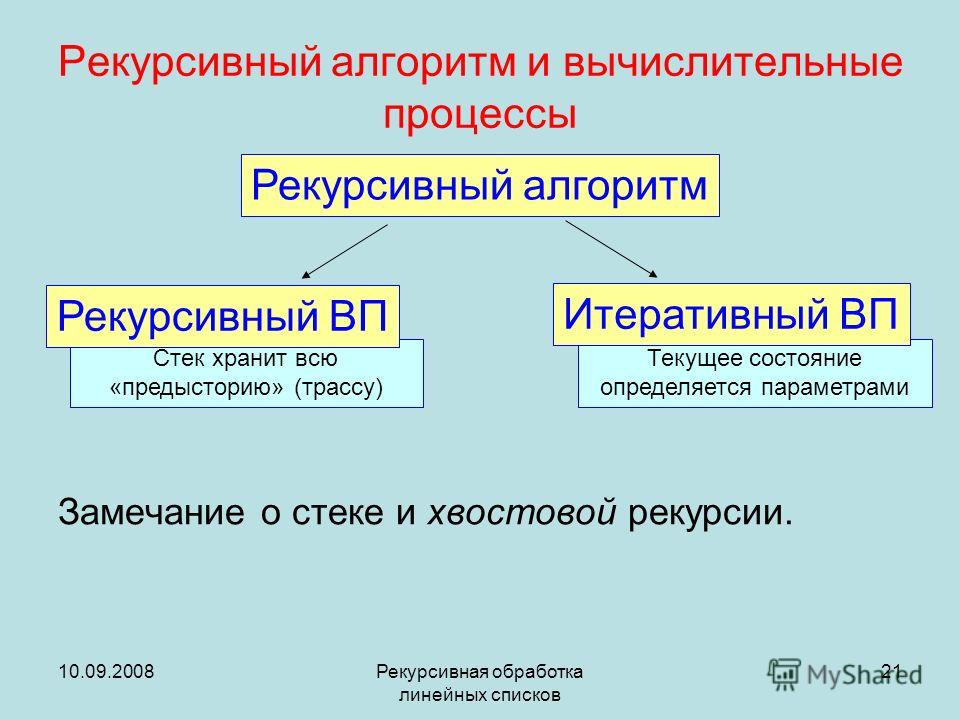 mit.edu/projects/190485662/.
mit.edu/projects/190485662/.
Все использованные в статье проекты собраны встудию «Рекурсия в Scratch»: https://scratch.mit.edu/studios/4413241/. В ней есть еще несколько интересных рекурсивных алгоритмов.
Рекурсивный алгоритм
Рекурсивный алгоритмРекурсивное определение
Предметы для изучения
- решение задачи с помощью рекурсивного алгоритма
- вычислительная функция с рекурсивным алгоритмом
- Проверка принадлежности к набору с помощью рекурсивного алгоритма
Содержимое
Рекурсивный алгоритм это алгоритм, который вызывает себя с «меньшими (или более простыми)» входными значениями и получает результат для текущего ввод путем применения простых операций к возвращаемому значению для меньшего (или более простого) ввода. В более общем случае, если проблема может быть решена использование решений для небольших версии одной и той же проблемы, а меньшие версии сводятся к легко решаемым случаям, тогда можно использовать рекурсивный алгоритм для решения этой проблемы. Например, элементы рекурсивно определенного множества или значение рекурсивно определенной функции.
можно получить рекурсивным алгоритмом.
Например, элементы рекурсивно определенного множества или значение рекурсивно определенной функции.
можно получить рекурсивным алгоритмом.Если набор или функция определены рекурсивно, то рекурсивный алгоритм вычисления его члены или значения отражают определение. Начальные шаги рекурсивного алгоритма соответствуют базовому предложению рекурсивного определения и идентифицируют базовые элементы. Затем за ними следуют шаги, соответствующие индуктивному предложению, которые сокращают вычисление элемента одного поколения к поколению элементы непосредственно предшествующего поколения.
В общем, рекурсивные компьютерные программы требуют больше памяти и вычислений по сравнению с итеративными алгоритмы, но они проще и во многих случаях являются естественным способом осмысления проблемы.
Пример 1: Алгоритм нахождения k -го четного натурального числа
Обратите внимание, что это можно очень легко решить, просто выведя 2 *( k — 1 ) для данного к . Однако цель здесь — проиллюстрировать основную идею рекурсии, а не решить проблему.
Однако цель здесь — проиллюстрировать основную идею рекурсии, а не решить проблему.
Алгоритм 1: Четное ( положительное целое число k )
Вход: k , положительное целое число
Вывод: k -е четное натуральное число (первое четное 0 )
Алгоритм:
если к = 1 , то вернуть 0 ;
иначе возврат Четный( k-1 ) + 2 .
Здесь вычисление Even( k ) сводится к вычислению Четный для меньшего входного значения, т.е. Четный( к-1 ). Четное( k ) в итоге становится Четное( 1 ) это 0 по первой строке. Например,
для вычисления Even( 3 ) , Алгоритм Even( k ) вызывается с к = 2 . При вычислении Четный( 2 ) , Алгоритм Even( k ) вызывается с помощью k = 1 . Поскольку Even( 1 ) = 0, 0 возвращается для вычисления Чет( 2 ) и Чет( 2 ) = Чет( 1 ) + 2 = 2 есть
полученный. Это значение 2 для Четный( 2 ) теперь возвращается для вычисления Четный( 3 ) и Чет ( 3 ) = Чет ( 2 ) + 2 = 4 получается.
Поскольку Even( 1 ) = 0, 0 возвращается для вычисления Чет( 2 ) и Чет( 2 ) = Чет( 1 ) + 2 = 2 есть
полученный. Это значение 2 для Четный( 2 ) теперь возвращается для вычисления Четный( 3 ) и Чет ( 3 ) = Чет ( 2 ) + 2 = 4 получается.
Как видно из сравнения этого алгоритма с рекурсивным определением
набор
неотрицательных четных чисел первая строка алгоритма соответствует
основному пункту определения, а вторая строка соответствует
к индуктивному предложению.
Для сравнения посмотрим, как та же задача может быть решена с помощью итеративного алгоритма.
Алгоритм 1-a: Четное ( положительное целое число k )
Ввод: k , положительное целое число
Вывод: k -е четное натуральное число (первое четное 0 )
Алгоритм:
int i , даже ;
i := 1 ;
даже := 0 ;
в то время как ( я < к ) {
четный := четный + 2 ;
i := i + 1 ;
}
вернуть даже .
Пример 2: Алгоритм вычисления k -й степени 2
Алгоритм 2 степень_2( натуральное число к)
Ввод: k , натуральное число
Выход: k -я степень числа 2
Алгоритм:
если к = 0 , то вернуть 1 ;
иначе вернуть 2*степень_2(k — 1 ) .
Для сравнения посмотрим, как та же задача может быть решена с помощью итеративного алгоритма.
Алгоритм 2-a степень_2( натуральное число k)
Ввод: k , натуральное число
Выход: k -я степень числа 2
Алгоритм:
int i , мощность ;
i := 0 ;
мощность := 1 ;
пока( i < k ) {
мощность := мощность * 2 ;
i := i + 1 ;
}
возврат мощность .
Следующий пример не имеет соответствующего рекурсивного определения. Он показывает рекурсивный способ решения проблемы.
Пример 3: Рекурсивный алгоритм последовательного поиска
Алгоритм 3 SeqSearch( L, i, j, x )
Ввод: L — массив, i и j — положительные целые числа, i j и x ключ
искать в L .
Вывод: Если x находится в L между индексами и и j , затем выведите его индекс, иначе выведите 0 .
Алгоритм:
если я j , затем
{
, если L ( i ) = x , , затем возврат и ;
иначе вернуть SeqSearch( л, я+1, у, х )
}
иначе вернуть 0 .
Рекурсивные алгоритмы также можно использовать для проверки объектов на принадлежность к множеству.
Пример 4: Алгоритм проверки того, является ли число натуральным x
Алгоритм 4 Естественный( число x )
Ввод: Число x
Вывод: » Да » если x является натуральным числом, иначе » Нет »
Алгоритм:
если x < 0 , тогда вернуть « Нет »
еще
если x = 0 , , то вернуть « Да »
иначе возврат Натуральный( x — 1 )
Пример 5: Алгоритм проверки того, является ли выражение w предложением (форма предложения)
Алгоритм 5 Предложение ( строка w )
Вход: Строка А w
Вывод: » Да » если w является предложением, иначе » Нет »
Алгоритм:
если w равно 1 (истина), 0 (ложь), или пропозициональная переменная, , затем , возврат « Да »
иначе если w = ~ w 1 , затем возврат Предложение ( с 1 )
иначе
если ( w = w 1 с 2 или с 1 с 2 или же с 1 с 2 или же с 1 с 2 )
и
Предложение ( w 1 ) = Да
и Предложение ( w 2 ) = Да
затем возврат Да
иначе вернуть Нет
конец
Проверьте свое понимание рекурсивного алгоритма
Укажите, какие из следующих утверждений верны, а какие нет.
Нажмите «Да» или «Нет» , затем «Отправить».
Далее — Первый принцип математической индукции
Вернуться к расписанию
Вернуться к оглавлению
Введение. Настоящий Python
Если вы знакомы с функциями в Python, то знаете, что одна функция часто вызывает другую. В Python функция также может вызывать сама себя! Функция, которая вызывает сама себя, называется 9.0762 рекурсивная , а метод использования рекурсивной функции называется рекурсией .
Может показаться странным, что функция вызывает сама себя, но многие типы программных задач лучше всего решать рекурсивно. Когда вы сталкиваетесь с такой проблемой, рекурсия становится незаменимым инструментом в вашем наборе инструментов.
К концу этого руководства вы поймете:
- Что означает рекурсивный вызов функции
- Как дизайн функций Python поддерживает рекурсию
- Какие факторы следует учитывать при выборе рекурсивного решения проблемы
- Как реализовать рекурсивную функцию в Python
Затем вы изучите несколько задач программирования на Python, в которых используется рекурсия, и сравните рекурсивное решение с сопоставимым нерекурсивным.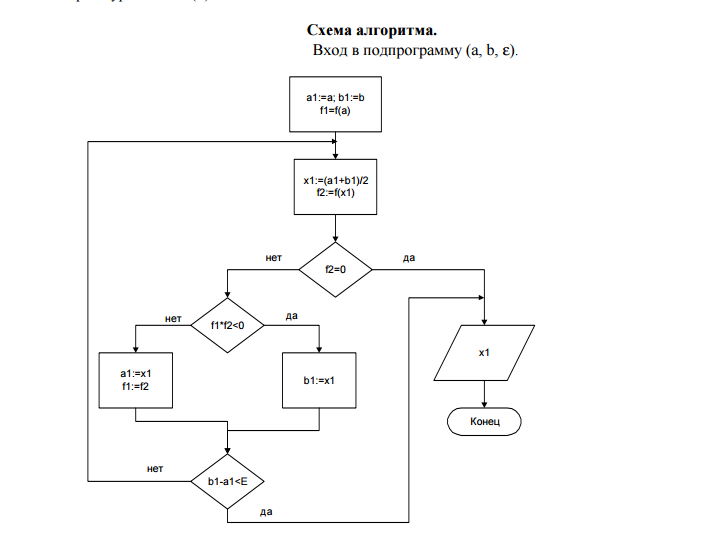
Что такое рекурсия?
Слово рекурсия происходит от латинского слова recurrere , что означает бежать или спешить назад, возвращаться, возвращаться или возвращаться. Вот некоторые онлайн-определения рекурсии:
- Dictionary.com : Действие или процесс возвращения или побега
- Викисловарь : Действие по определению объекта (обычно функции) с точки зрения самого объекта
- Бесплатный словарь : метод определения последовательности объектов, таких как выражение, функция или набор, где задано некоторое количество начальных объектов, и каждый последующий объект определяется в терминах предшествующих объектов
Рекурсивное определение — это определение, в котором определяемый термин появляется в самом определении. Самореферентные ситуации часто возникают в реальной жизни, даже если они не сразу распознаются как таковые. Например, предположим, что вы хотите описать группу людей, которые составляют ваших предков. Вы можете описать их так:
Вы можете описать их так:
Обратите внимание, как определяемое понятие предков проявляется в собственном определении. Это рекурсивное определение.
В программировании рекурсия имеет очень точное значение. Это относится к методу кодирования, при котором функция вызывает сама себя.
Удалить рекламу
Зачем использовать рекурсию?
Большинство задач программирования можно решить без рекурсии. Так что, строго говоря, рекурсия обычно не нужна.
Однако в некоторых ситуациях самореферентное определение особенно удобно для — например, определение предков, показанное выше. Если бы вы разрабатывали алгоритм для обработки такого случая программно, рекурсивное решение, вероятно, было бы чище и лаконичнее.
Еще одним хорошим примером является обход древовидных структур данных. Поскольку это вложенные структуры, они легко поддаются рекурсивному определению. Нерекурсивный алгоритм обхода вложенной структуры, вероятно, будет несколько неуклюжим, тогда как рекурсивное решение будет относительно элегантным. Пример этого появится позже в этом руководстве.
Нерекурсивный алгоритм обхода вложенной структуры, вероятно, будет несколько неуклюжим, тогда как рекурсивное решение будет относительно элегантным. Пример этого появится позже в этом руководстве.
С другой стороны, рекурсия подходит не для всех ситуаций. Вот некоторые другие факторы, которые следует учитывать:
- Для некоторых задач рекурсивное решение хотя и возможно, но будет скорее неудобным, чем элегантным.
- Рекурсивные реализации часто потребляют больше памяти, чем нерекурсивные.
- В некоторых случаях использование рекурсии может привести к увеличению времени выполнения.
Обычно решающим фактором является читабельность кода. Но это зависит от обстоятельств. Представленные ниже примеры должны помочь вам понять, когда следует выбирать рекурсию.
Рекурсия в Python
Когда вы вызываете функцию в Python, интерпретатор создает новое локальное пространство имен, чтобы имена, определенные в этой функции, не конфликтовали с идентичными именами, определенными где-либо еще. Одна функция может вызывать другую, и даже если они обе определяют объекты с одним и тем же именем, все работает нормально, потому что эти объекты существуют в разных пространства имен .
Одна функция может вызывать другую, и даже если они обе определяют объекты с одним и тем же именем, все работает нормально, потому что эти объекты существуют в разных пространства имен .
То же самое верно, если несколько экземпляров одной и той же функции выполняются одновременно. Например, рассмотрим следующее определение:
функция определения():
х = 10
функция()
Когда function() выполняется в первый раз, Python создает пространство имен и присваивает x значение 10 в этом пространстве имен. Затем function() вызывает себя рекурсивно. При втором запуске function() интерпретатор создает второе пространство имен и присваивает 10 до x там же. Эти два экземпляра имени x отличаются друг от друга и могут сосуществовать без конфликтов, поскольку они находятся в разных пространствах имен.
К сожалению, запуск function() в его нынешнем виде дает результат, который не вдохновляет, как показывает следующая обратная трассировка:
>>>
>>> функция() Traceback (последний последний вызов): Файл "", строка 1, в Файл " ", строка 3, в функции Файл " ", строка 3, в функции Файл " ", строка 3, в функции [Предыдущая строка повторяется 9еще 96 раз] RecursionError: превышена максимальная глубина рекурсии
Как написано, function() теоретически будет продолжаться вечно, вызывая себя снова и снова без каких-либо возвратов вызовов. На практике, конечно, ничто не вечно. У вашего компьютера ограниченное количество памяти, и в конце концов она закончится.
На практике, конечно, ничто не вечно. У вашего компьютера ограниченное количество памяти, и в конце концов она закончится.
Python не позволяет этому случиться. Интерпретатор ограничивает максимальное количество раз, которое функция может вызывать сама себя рекурсивно, и когда она достигает этого предела, она вызывает Исключение RecursionError , как вы видите выше.
Техническое примечание: Вы можете узнать предел рекурсии Python с помощью функции из модуля sys с именем getrecursionlimit() :
>>>
>>> from sys import getrecursionlimit >>> получить предел рекурсии() 1000
Вы также можете изменить его с помощью setrecursionlimit() :
>>>
>>> from sys import setrecursionlimit >>> установить лимит рекурсии (2000) >>> получить предел рекурсии() 2000 г.
Вы можете сделать его довольно большим, но вы не можете сделать его бесконечным.
Нет особого смысла в том, чтобы функция без разбора рекурсивно вызывала сама себя без конца. Это напоминает инструкции, которые иногда можно найти на бутылках с шампунем: «Вспенить, смыть, повторить». Если бы вы буквально следовали этим инструкциям, вы бы мыли волосы шампунем вечно!
Эта логическая ошибка, очевидно, пришла в голову некоторым производителям шампуня, потому что на некоторых бутылках с шампунем вместо этого написано: «Вспенить, смыть, повторить 9».0798 при необходимости ». Это обеспечивает условие завершения инструкций. Предположительно, вы в конечном итоге почувствуете, что ваши волосы достаточно чистые, чтобы считать дополнительные повторения ненужными. После этого мытье головы можно прекратить.
Точно так же функция, которая вызывает сама себя рекурсивно, должна иметь план остановки. Рекурсивные функции обычно следуют этому шаблону:
.- Существует один или несколько базовых случаев, которые можно решить напрямую без необходимости дальнейшей рекурсии.

- Каждый рекурсивный вызов приближает решение к базовому варианту.
Теперь вы готовы увидеть, как это работает, на нескольких примерах.
Удаление рекламы
Начало работы: Обратный отсчет до нуля
Первый пример — это функция с именем countdown() , которая принимает положительное число в качестве аргумента и печатает числа от указанного аргумента до нуля:
>>>
>>> обратный отсчет (n): ... печать (н) ... если n == 0: ... return # Завершить рекурсию ... еще: ... countdown(n - 1) # Рекурсивный вызов ... >>> обратный отсчет(5) 5 4 3 2 1 0
Обратите внимание, как обратный отсчет() соответствует описанной выше парадигме рекурсивного алгоритма:
- В базовом случае
nравно нулю, и в этот момент рекурсия останавливается. - В рекурсивном вызове аргумент на единицу меньше, чем текущее значение
n, поэтому каждая рекурсия приближается к базовому варианту.
Примечание: Для простоты обратный отсчет() не проверяет правильность своего аргумента. Если п является либо нецелым, либо отрицательным, вы получите исключение RecursionError , поскольку базовый случай никогда не достигается.
Версия countdown() , показанная выше, четко выделяет базовый случай и рекурсивный вызов, но есть более краткий способ выразить это:
обратный отсчет (n):
печать (н)
если п > 0:
обратный отсчет (n - 1)
Вот одна из возможных нерекурсивных реализаций для сравнения:
>>>
>>> обратный отсчет (n): ... пока n >= 0: ... печать (н) ... п -= 1 ... >>> обратный отсчет(5) 5 4 3 2 1 0
Это тот случай, когда нерекурсивное решение не менее ясно и интуитивно понятно, чем рекурсивное, а может быть и лучше.
Вычислить факториал
В следующем примере используется математическое понятие факториала. Факториал натурального числа n , обозначаемый как n !, определяется следующим образом:
Факториал натурального числа n , обозначаемый как n !, определяется следующим образом:
Другими словами, n ! является произведением всех целых чисел от 1 до n включительно.
Факториал настолько поддается рекурсивному определению, что тексты по программированию почти всегда включают его в качестве одного из первых примеров. Вы можете выразить определение n ! рекурсивно так:
Как и в примере, показанном выше, существуют базовые случаи, которые можно решить без рекурсии. Более сложными случаями являются редуктивных , что означает, что они сводятся к одному из базовых случаев:
- Базовые случаи ( n = 0 или n = 1) решаемы без рекурсии.
- Для значений n больше 1, n ! определяется в терминах ( n — 1)!, поэтому рекурсивное решение постепенно приближается к базовому случаю.
Например, рекурсивное вычисление 4! выглядит так:
Рекурсивный расчет 4! Вычисления 4!, 3! и 2! приостановить, пока алгоритм не достигнет базового случая, когда n = 1. В этот момент 1! вычисляется без дальнейшей рекурсии, и отложенные вычисления выполняются до завершения.
В этот момент 1! вычисляется без дальнейшей рекурсии, и отложенные вычисления выполняются до завершения.
Удалить рекламу
Определить факториальную функцию Python
Вот рекурсивная функция Python для вычисления факториала. Обратите внимание, насколько оно лаконичное и насколько хорошо оно отражает приведенное выше определение:
.>>>
>>> def factorial(n): ... вернуть 1, если n <= 1 иначе n * factorial(n - 1) ... >>> факториал(4) 24
Небольшое украшение этой функции некоторыми операторами print() дает более четкое представление о последовательности вызова и возврата:
>>>
>>> def factorial(n):
... print(f"factorial() вызывается с n = {n}")
... return_value = 1, если n <= 1, иначе n * factorial(n -1)
... print(f"-> factorial({n}) возвращает {return_value}")
... вернуть возвращаемое_значение
. ..
>>> факториал(4)
factorial() вызывается с n = 4
factorial() вызывается с n = 3
factorial() вызывается с n = 2
factorial() вызывается с n = 1
-> факториал(1) возвращает 1
-> факториал(2) возвращает 2
-> факториал(3) возвращает 6
-> факториал(4) возвращает 24
24
..
>>> факториал(4)
factorial() вызывается с n = 4
factorial() вызывается с n = 3
factorial() вызывается с n = 2
factorial() вызывается с n = 1
-> факториал(1) возвращает 1
-> факториал(2) возвращает 2
-> факториал(3) возвращает 6
-> факториал(4) возвращает 24
24
Обратите внимание, как складываются все рекурсивные вызовы . Функция вызывается последовательно с n = 4 , 3 , 2 и 1 до возврата любого из вызовов. Наконец, когда n равно 1 , проблема может быть решена без рекурсии. Затем каждый из сложенных рекурсивных вызовов раскручивается обратно, возвращая 1 , 2 , 6 и, наконец, 24 из самого внешнего вызова.
Рекурсия здесь не нужна. Вы можете реализовать factorial() итеративно, используя цикл for :
>>>
>>> def factorial(n): ... возвращаемое_значение = 1 ... для i в диапазоне (2, n + 1): ... возвращаемое_значение *= я ... вернуть возвращаемое_значение ... >>> факториал(4) 24
Вы также можете реализовать факториал, используя Python reduce() , который вы можете импортировать из модуля functools :
>>>
>>> из functools импортировать уменьшить >>> по факториалу (n): ... вернуть уменьшить (лямбда x, y: x * y, диапазон (1, n + 1) или [1]) ... >>> факториал(4) 24
Опять же, это показывает, что если проблема разрешима с помощью рекурсии, вероятно, также будет несколько жизнеспособных нерекурсивных решений. Обычно вы выбираете на основе того, какой из них приводит к наиболее читаемому и интуитивно понятному коду.
Другим фактором, который необходимо учитывать, является скорость выполнения. Между рекурсивными и нерекурсивными решениями могут быть значительные различия в производительности. В следующем разделе вы немного подробнее изучите эти различия.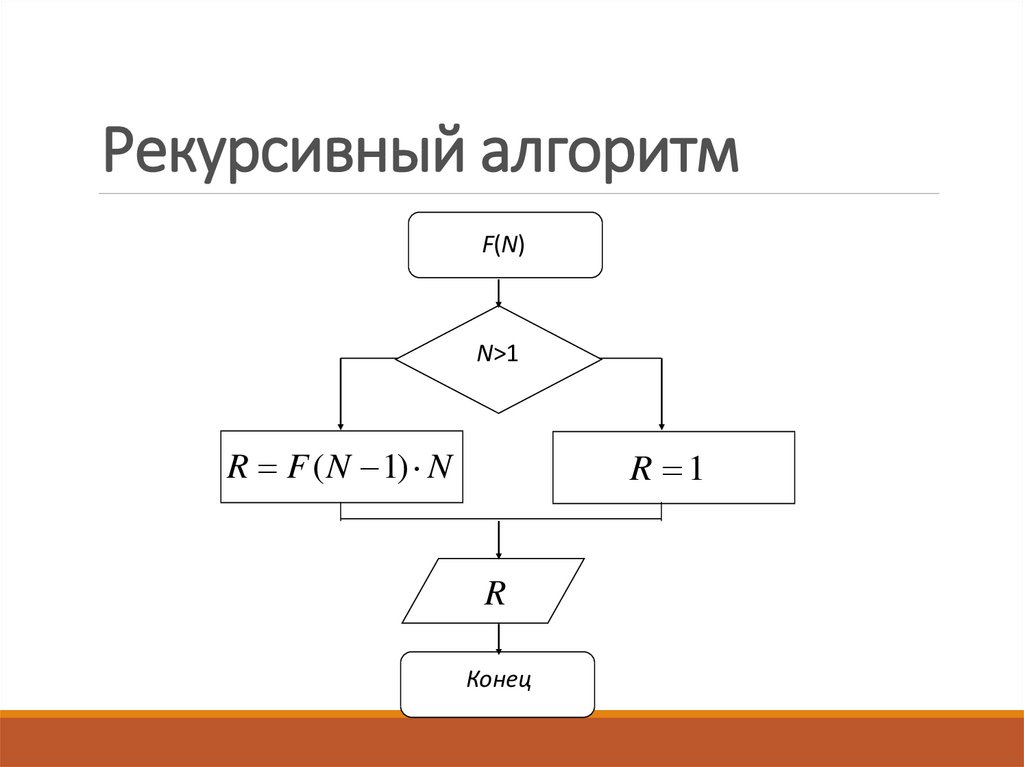
Сравнение скорости факториальных реализаций
Чтобы оценить время выполнения, вы можете использовать функцию с именем timeit() из модуля, который также называется timeit . Эта функция поддерживает ряд различных форматов, но в этом руководстве вы будете использовать следующий формат:
timeit(<команда>, setup=, число=<итераций>)
timeit() сначала выполняет команды, содержащиеся в указанных <строка_установки> . Затем он выполняет <команда> заданное количество <итераций> и сообщает общее время выполнения в секундах:
>>>
>>> from timeit импорт timeit
>>> timeit("print(string)", setup="string='foobar'", number=100)
фубар
фубар
фубар
.
. [100 повторений]
.
фубар
0,03347089999988384
Здесь параметр setup присваивает строке значение 'фубар' . Затем
Затем timeit() печатает строку сто раз. Общее время выполнения составляет чуть более 3/100 секунды.
В приведенных ниже примерах используется timeit() для сравнения рекурсивной, итеративной и reduce() реализаций факториала, описанных выше. В каждом случае setup_string содержит строку настройки, которая определяет соответствующую функцию factorial() . timeit() затем выполняет factorial(4) в общей сложности десять миллионов раз и сообщает об общем выполнении.
Во-первых, вот рекурсивная версия:
>>>
>>> setup_string = """
... печать ("Рекурсивно:")
... факториал по умолчанию (n):
... вернуть 1, если n <= 1 иначе n * factorial(n - 1)
... """
>>> из timeit импортировать timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Рекурсивный:
4.957105500000125
Далее идет итеративная реализация:
>>>
>>> setup_string = """ ... print("Итеративно:") ... факториал по умолчанию (n): ... возвращаемое_значение = 1 ... для i в диапазоне (2, n + 1): ... возвращаемое_значение *= я ... вернуть возвращаемое_значение ... """ >>> из timeit импортировать timeit >>> timeit("factorial(4)", setup=setup_string, number=10000000) Итеративный: 3.733752099999947
Наконец, вот версия, которая использует reduce() :
>>>
>>> setup_string = """
... из functools импортировать уменьшить
... печать ("уменьшить():")
... факториал по умолчанию (n):
... вернуть уменьшить (лямбда x, y: x * y, диапазон (1, n + 1) или [1])
... """
>>> из timeit импортировать timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
уменьшать():
8.101526299999932
В этом случае итеративная реализация является самой быстрой, хотя рекурсивное решение не сильно отстает. Метод с использованием reduce() является самым медленным. Ваш пробег, вероятно, изменится, если вы попробуете эти примеры на своей машине. Вы, конечно, не получите такое же время, и вы можете даже не получить тот же рейтинг.
Вы, конечно, не получите такое же время, и вы можете даже не получить тот же рейтинг.
Имеет ли это значение? Существует разница почти в четыре секунды во времени выполнения между итеративной реализацией и той, которая использует reduce() , но чтобы увидеть это, потребовалось десять миллионов вызовов.
Если вы будете вызывать функцию много раз, вам может потребоваться учитывать скорость выполнения при выборе реализации. С другой стороны, если функция будет запускаться относительно редко, то разница во времени выполнения, вероятно, будет незначительной. В этом случае вам лучше выбрать ту реализацию, которая кажется наиболее ясно выражающей решение проблемы.
Для факториала приведенные выше значения времени указывают на разумный выбор рекурсивной реализации.
Откровенно говоря, если вы программируете на Python, вам вообще не нужно реализовывать функцию факториала. Он уже доступен в стандартном модуле math :
>>>
>>> из факториала импорта математики >>> факториал(4) 24
Возможно, вам будет интересно узнать, как это работает в тесте синхронизации:
>>>
>>> setup_string = "из математического импорта факториала"
>>> из timeit импортировать timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
0,3724050999999946
Вау! math. работает лучше, чем лучшая из трех других реализаций, показанных выше, примерно в 10 раз. factorial()
factorial()
Функция, реализованная на C, практически всегда будет быстрее, чем соответствующая функция, реализованная на чистом Python.
Удаление рекламы
Просмотр вложенного списка
Следующий пример включает посещение каждого элемента в структуре вложенного списка. Рассмотрим следующий список Python:
имен = [
"Адам",
[
"Боб",
[
"Чет",
"Кошка",
],
"Барб",
"Берт"
],
"Алекс",
[
"Беа",
"Билл"
],
"Анна"
]
Как показано на следующей диаграмме, имен содержит два подсписка. Сам первый из этих подсписков содержит еще один подсписок:
Предположим, вы хотите подсчитать количество листовых элементов в этом списке — объектов самого низкого уровня str — как если бы вы сгладили список. Листовые элементы
Листовые элементы «Адам» , «Боб» , «Чет» , «Кот» , «Барб» , «Берт» , «Алекс2», 90 "Беа" , "Билл" и "Энн" , поэтому ответ должен быть 10 .
Простой вызов len() из списка не дает правильного ответа:
>>>
>>> лен(имена) 5
len() подсчитывает объекты на верхнем уровне имен , которые являются тремя листовыми элементами "Адам" , "Алекс" и "Энн" и два подсписка ["Боб" , ["Чет", "Кот"], "Барб", "Берт"] и ["Би", "Билл"] :
>>>
>>> для индекса, элемент в перечислении (имена): ... печать (индекс, элемент) ... 0 Адам 1 ['Боб', ['Чет', 'Кэт'], 'Барб', 'Берт'] 2 Алекс 3 ['Би', 'Билл'] 4 Энн
Здесь вам нужна функция, которая проходит через всю структуру списка, включая подсписки. Алгоритм примерно такой:
Алгоритм примерно такой:
- Пройдитесь по списку, изучая каждый пункт по очереди.
- Если вы найдете конечный элемент, добавьте его к накопленному счетчику.
- Если вы столкнулись с подсписком, сделайте следующее:
- Перейдите в этот подсписок и аналогичным образом пройдитесь по нему.
- После того, как вы исчерпали подсписок, вернитесь назад, добавьте элементы из подсписка к накопленному счетчику и возобновите просмотр родительского списка с того места, где вы остановились.
Обратите внимание на самореферентный характер этого описания: Просмотрите список . Если вы встретите подсписок, то аналогично пройдитесь по этому списку . Эта ситуация требует рекурсии!
Рекурсивный обход вложенного списка
Рекурсия очень хорошо подходит для этой задачи. Чтобы решить эту проблему, вы должны иметь возможность определить, является ли данный элемент списка конечным элементом или нет. Для этого вы можете использовать встроенную функцию Python isinstance() .
В случае списка имен , если элемент является экземпляром типа list , то это подсписок. В противном случае это конечный элемент:
>>>
>>> имена ['Адам', ['Боб', ['Чет', 'Кэт'], 'Барб', 'Берт'], 'Алекс', ['Би', 'Билл'], 'Энн'] >>> имена[0] 'Адам' >>> isinstance(имена[0], список) ЛОЖЬ >>> имена[1] ['Боб', ['Чет', 'Кэт'], 'Барб', 'Берт'] >>> isinstance(имена[1], список) Истинный >>> имена[1][1] ['Чет', 'Кот'] >>> isinstance(имена[1][1], список) Истинный >>> имена[1][1][0] 'Чет' >>> isinstance(имена[1][1][0], список) ЛОЖЬ
Теперь у вас есть инструменты для реализации функции, которая подсчитывает конечные элементы в списке, рекурсивно учитывая подсписки:
по определению count_leaf_items (item_list):
"""Рекурсивно считает и возвращает
количество листовых элементов в (потенциально
вложенный) список.
"""
количество = 0
для элемента в item_list:
если isinstance (элемент, список):
count += count_leaf_items(предмет)
еще:
количество += 1
количество возвратов
Если вы запустите count_leaf_items() для нескольких списков, включая список имен , определенный выше, вы получите следующее:
>>>
>>> count_leaf_items([1, 2, 3, 4]) 4 >>> count_leaf_items([1, [2.1, 2.2], 3]) 4 >>> count_leaf_items([]) 0 >>> count_leaf_items(имена) 10 >>> # Успех!
Как и в примере с факториалом, добавление некоторых операторов print() помогает продемонстрировать последовательность рекурсивных вызовов и возвращаемых значений:
1def count_leaf_items(item_list):
2 """Рекурсивно считает и возвращает
3 количество листовых элементов в (потенциально
4 вложенных) списка.
5 """
6 print(f"Список: {item_list}")
7 количество = 0
8 для элемента в item_list:
9если isinstance (элемент, список):
10 print("Встреченный подсписок")
11 count += count_leaf_items(предмет)
12 еще:
13 print(f"Счетный лист \"{item}\"")
14 счет += 1
15
16 print(f"-> Количество возвращений {count}")
17 возвратов
Вот краткий обзор того, что происходит в приведенном выше примере:
- Строка 9:
isinstance(item, list)isinstance(item, list) isTrue, поэтомуcount_leaf_items()нашел подсписок.
- Строка 11: Функция рекурсивно вызывает себя для подсчета элементов в подсписке, а затем добавляет результат к накапливаемой сумме.
- Строка 12:
isinstance(item, list)isFalse, поэтомуcount_leaf_items()обнаружил конечный элемент. - Строка 14: Функция увеличивает накопительную сумму на единицу для учета конечного элемента.
Примечание: Для простоты эта реализация предполагает, что список передается в count_leaf_items() содержит только конечные элементы или подсписки, а не любой другой тип составного объекта, такого как словарь или кортеж.
Вывод из count_leaf_items() при выполнении в списке имен теперь выглядит следующим образом:
>>>
>>> count_leaf_items(имена) Список: ['Адам', ['Боб', ['Чет', 'Кэт'], 'Барб', 'Берт'], 'Алекс', ['Би', 'Билл'], 'Энн'] Счетный листочек "Адам" Встреченный подсписок Список: ['Боб', ['Чет', 'Кэт'], 'Барб', 'Берт'] Счетный листочек "Боб" Встреченный подсписок Список: ['Чет', 'Кот'] Счетный листовой предмет "Чет" Счетный листочек "Кошка" -> Возвращаемый счет 2 Счетный лист "Барб" Счетный листочек "Берт" -> Возвращаемый счет 5 Счетный листочек "Алекс" Встреченный подсписок Список: ['Би', 'Билл'] Счетный листочек "Беа" Счетный листовой предмет "Купюра" -> Возвращаемый счет 2 Счетный листочек "Энн" -> Возвращаемый счет 10 10
Каждый раз, когда вызов count_leaf_items() завершается, он возвращает количество листовых элементов, подсчитанных им в переданном ему списке.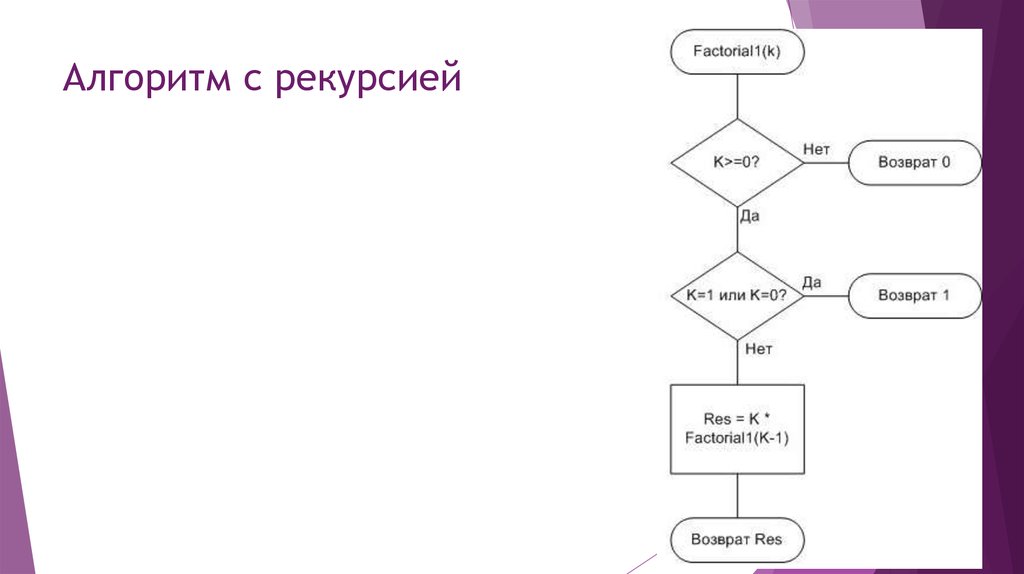 Вызов верхнего уровня возвращает
Вызов верхнего уровня возвращает 10 , как и должно быть.
Удаление рекламы
Нерекурсивный обход вложенного списка
Как и в других примерах, показанных до сих пор, этот обход списка не требует рекурсии. Вы также можете выполнить это итеративно. Вот один из вариантов:
по определению count_leaf_items (item_list):
"""Нерекурсивно считает и возвращает
количество листовых элементов в (потенциально
вложенный) список.
"""
количество = 0
стек = []
текущий_список = список_элементов
я = 0
пока верно:
если я == len(current_list):
если текущий_список == список_элементов:
количество возвратов
еще:
текущий_список, я = stack.pop()
я += 1
Продолжать
если есть экземпляр (текущий_список [i], список):
stack.append([current_list, я])
текущий_список = текущий_список[i]
я = 0
еще:
количество += 1
я += 1
Если вы запустите эту нерекурсивную версию count_leaf_items() в тех же списках, что и ранее, вы получите те же результаты:
>>>
>>> count_leaf_items([1, 2, 3, 4]) 4 >>> count_leaf_items([1, [2.1, 2.2], 3]) 4 >>> count_leaf_items([]) 0 >>> count_leaf_items(имена) 10 >>> # Успех!
Используемая здесь стратегия использует стек для обработки вложенных подсписков. Когда эта версия count_leaf_items() встречает подсписок, он помещает текущий список и текущий индекс в этом списке в стек. После подсчета подсписка функция извлекает родительский список и индекс из стека, чтобы продолжить подсчет с того места, где он остановился.
Фактически то же самое происходит и в рекурсивной реализации. Когда вы вызываете функцию рекурсивно, Python сохраняет состояние исполняемого экземпляра в стеке, чтобы рекурсивный вызов мог выполняться. Когда рекурсивный вызов завершается, состояние извлекается из стека, чтобы прерванный экземпляр мог возобновиться. Это та же концепция, но с рекурсивным решением, Python выполняет работу по сохранению состояния за вас.
Обратите внимание, насколько лаконичен и удобочитаем рекурсивный код по сравнению с нерекурсивной версией:
Рекурсивный и нерекурсивный обход вложенных списков Это тот случай, когда использование рекурсии определенно является преимуществом.
Обнаружение палиндромов
Выбор того, следует ли использовать рекурсию для решения проблемы, во многом зависит от характера проблемы. Факториал, например, естественным образом преобразуется в рекурсивную реализацию, но и итеративное решение также довольно простое. В таком случае это, возможно, жеребьевка.
Проблема обхода списка — это отдельная история. В этом случае рекурсивное решение очень элегантно, а нерекурсивное в лучшем случае громоздко.
Для следующей проблемы использование рекурсии, возможно, глупо.
Палиндром — это слово, которое одинаково читается как в прямом, так и в обратном направлении. Примеры включают следующие слова:
- Гоночная машина
- Уровень
- Каяк
- Оживитель
- Цивик
Если бы вас попросили разработать алгоритм для определения того, является ли строка палиндромной, вы, вероятно, предложили бы что-то вроде «Переверните строку и посмотрите, совпадает ли она с исходной». Вы не можете быть намного яснее, чем это.
Вы не можете быть намного яснее, чем это.
Еще более полезно то, что синтаксис среза Python [::-1] для обращения строки обеспечивает удобный способ ее кодирования:
>>>
>>> определение is_palindrome(word):
... """Возвращает True, если слово является палиндромом, False, если нет."""
... вернуть слово == слово[::-1]
...
>>> is_palindrome("foo")
ЛОЖЬ
>>> is_palindrome("гоночная машина")
Истинный
>>> is_palindrome("троглодит")
ЛОЖЬ
>>> is_palindrome("гражданское")
Истинный
Это ясно и кратко. Вряд ли стоит искать альтернативу. Но просто для удовольствия рассмотрим это рекурсивное определение палиндрома:
.- Базовые случаи: Пустая строка и строка, состоящая из одного символа, по своей сути палиндромны.
- Редуктивная рекурсия: Строка длины два или больше является палиндромом, если она удовлетворяет обоим следующим критериям:
- Первый и последний символы совпадают.

- Подстрока между первым и последним символом является палиндромом.
- Первый и последний символы совпадают.
Нарезка и здесь вам в помощь. Для строки word индексация и нарезка дают следующие подстроки:
- Первый символ
word[0]. - Последний символ
слово[-1]. - Подстрока между первым и последним символами:
word[1:-1].
Итак, вы можете определить is_palindrome() рекурсивно так:
>>>
>>> определение is_palindrome(word):
... """Возвращает True, если слово является палиндромом, False, если нет."""
... если длина (слово) <= 1:
... вернуть Истина
... еще:
... вернуть слово[0] == слово[-1] и is_palindrome(слово[1:-1])
...
>>> # Базовые случаи
>>> is_palindrome("")
Истинный
>>> is_palindrome("а")
Истинный
>>> # Рекурсивные случаи
>>> is_palindrome("foo")
ЛОЖЬ
>>> is_palindrome("гоночная машина")
Истинный
>>> is_palindrome("троглодит")
ЛОЖЬ
>>> is_palindrome("гражданское")
Истинный
Рекурсивное мышление — интересное упражнение, даже если в этом нет особой необходимости.
Удалить рекламу
Сортировка с быстрой сортировкой
Последний представленный пример, как и обход вложенного списка, является хорошим примером проблемы, которая естественным образом предполагает рекурсивный подход. Алгоритм быстрой сортировки — это эффективный алгоритм сортировки, разработанный британским ученым-компьютерщиком Тони Хоаром в 1959 году.
Быстрая сортировка — это алгоритм «разделяй и властвуй». Предположим, у вас есть список объектов для сортировки. Вы начинаете с выбора элемента в списке, который называется 9.0762 шарнир поз. Это может быть любой элемент списка. Затем вы разбиваете список на два подсписка на основе элемента сводки и рекурсивно сортируете подсписки.
Шаги алгоритма следующие:
- Выберите элемент сводки.
- Разделить список на два подсписка:
- Те элементы, которые меньше основного элемента
- Те элементы, которые больше, чем основной элемент
- Быстрая рекурсивная сортировка подсписков.

Каждое разбиение создает подсписки меньшего размера, поэтому алгоритм является редуктивным. Базовые случаи возникают, когда подсписки либо пусты, либо содержат один элемент, поскольку они по своей сути отсортированы.
Выбор основного элемента
Алгоритм быстрой сортировки будет работать независимо от того, какой элемент списка является основным. Но некоторые варианты лучше других. Помните, что при разбиении создаются два подсписка: один с элементами, которые меньше, чем элемент сводки, и один с элементами, которые больше, чем элемент сводки. В идеале два подсписка должны иметь примерно одинаковую длину.
Представьте, что ваш исходный список для сортировки содержит восемь элементов. Если каждое разбиение приводит к подспискам примерно одинаковой длины, то вы можете достичь базовых случаев за три шага:
Оптимальное разбиение, список из восьми элементов На другом конце спектра, если ваш выбор сводного элемента особенно неудачен, каждое разбиение приводит к одному подсписку, который содержит все исходные элементы, кроме основного элемента, и еще один подсписок, который пуст. В этом случае требуется семь шагов, чтобы сократить список до базовых случаев:
В этом случае требуется семь шагов, чтобы сократить список до базовых случаев:
Алгоритм быстрой сортировки будет более эффективным в первом случае. Но вам нужно знать кое-что заранее о характере данных, которые вы сортируете, чтобы систематически выбирать оптимальные сводные элементы. В любом случае, не существует какого-то одного варианта, который был бы лучшим для всех случаев. Так что, если вы пишете функцию быстрой сортировки для обработки общего случая, выбор сводного элемента несколько произволен.
Первый элемент в списке является обычным выбором, как и последний элемент. Они будут работать нормально, если данные в списке распределены довольно случайным образом. Однако, если данные уже отсортированы или даже почти отсортированы, это приведет к неоптимальному разделению, как показано выше. Чтобы избежать этого, некоторые алгоритмы быстрой сортировки выбирают средний элемент списка в качестве элемента сводной таблицы.
Другой вариант — найти медиану первого, последнего и среднего элементов в списке и использовать ее в качестве опорного элемента. Это стратегия, используемая в примере кода ниже.
Реализация разделения
После того, как вы выбрали элемент сводки, следующим шагом будет разделение списка. Опять же, цель состоит в том, чтобы создать два подсписка, один из которых содержит элементы, которые меньше элемента сводки, а другой содержит элементы, которые больше.
Это можно сделать прямо на месте. Другими словами, меняя местами элементы, вы можете перетасовывать элементы в списке до тех пор, пока главный элемент не окажется в середине, все меньшие элементы окажутся слева от него, а все большие элементы — справа. Затем, когда вы рекурсивно сортируете подсписки, вы передаете фрагменты списка слева и справа от элемента сводки.
В качестве альтернативы вы можете использовать возможности Python по работе со списками для создания новых списков вместо того, чтобы работать с исходным списком на месте. Это подход, используемый в приведенном ниже коде. Алгоритм следующий:
Это подход, используемый в приведенном ниже коде. Алгоритм следующий:
- Выберите элемент сводки, используя метод медианы трех, описанный выше.
- Используя элемент сводки, создайте три подсписка:
- Элементы в исходном списке, которые меньше, чем элемент сводки
- Сам поворотный элемент
- Элементы в исходном списке больше, чем элемент сводки
- Рекурсивная быстрая сортировка списков 1 и 3.
- Объединить все три списка вместе.
Обратите внимание, что это включает в себя создание третьего подсписка, который содержит сам элемент сводки. Одним из преимуществ этого подхода является то, что он легко обрабатывает случай, когда элемент сводки появляется в списке более одного раза. В этом случае список 2 будет содержать более одного элемента.
Удаление рекламы
Использование реализации Quicksort
Теперь, когда основа готова, вы готовы перейти к алгоритму быстрой сортировки. Вот код Python:
Вот код Python:
1статистика импорта 2 Быстрая сортировка 3def (числа): 4, если len(числа) <= 1: 5 номеров возврата 6 еще: 7 пивот = статистика.медиана( 8 [ 9 номеров[0], 10 чисел[len(числа) // 2], 11 номеров[-1] 12] 13 ) 14 items_less, pivot_items, items_greater = ( 15 [n вместо n в цифрах, если n < опорная точка], 16 [n вместо n в цифрах, если n == точка опоры], 17 [n вместо n в цифрах, если n > точки опоры] 18 ) 1920 возврат ( 21 быстрая сортировка(items_less) + 22 сводных_элемента + 23 быстрая сортировка (items_greater) 24 )
Вот что делает каждый раздел quicksort() :
- Строка 4: Базовые случаи, когда список либо пуст, либо содержит только один элемент
- Строки с 7 по 13: Расчет сводного элемента методом медианы трех
- Строки с 14 по 18: Создание трех списков разделов
- Строки с 20 по 24: Рекурсивная сортировка и повторная сборка списков разделов
Примечание: Преимущество этого примера в том, что он краток и относительно удобочитаем. Однако это не самая эффективная реализация. В частности, создание списков разделов в строках с 14 по 18 требует повторения списка три раза, что не оптимально с точки зрения времени выполнения.
Однако это не самая эффективная реализация. В частности, создание списков разделов в строках с 14 по 18 требует повторения списка три раза, что не оптимально с точки зрения времени выполнения.
Вот несколько примеров quicksort() в действии:
>>>
>>> # Базовые случаи >>> быстрая сортировка([]) [] >>> быстрая сортировка([42]) [42] >>> # Рекурсивные случаи >>> быстрая сортировка([5, 2, 6, 3]) [2, 3, 5, 6] >>> быстрая сортировка([10, -3, 21, 6, -8]) [-8, -3, 6, 10, 21]
В целях тестирования вы можете определить короткую функцию, которая генерирует список случайных чисел между 1 и 100 :
случайный импорт
def get_random_numbers (длина, минимум = 1, максимум = 100):
числа = []
для _ в диапазоне (длина):
числа.добавление(случайное.случайное(минимум, максимум))
возвращаемые числа
Теперь вы можете использовать get_random_numbers() для проверки quicksort() :
>>>
>>> числа = get_random_numbers(20) >>> номера [24, 4, 67, 71, 84, 63, 100, 94, 53, 64, 19, 89, 48, 7, 31, 3, 32, 76, 91, 78] >>> быстрая сортировка(числа) [3, 4, 7, 19, 24, 31, 32, 48, 53, 63, 64, 67, 71, 76, 78, 84, 89, 91, 94, 100] >>> числа = get_random_numbers(15, -50, 50) >>> номера [-2, 14, 48, 42, -48, 38, 44, -25, 14, -14, 41, -30, -35, 36, -5] >>> быстрая сортировка(числа) [-48, -35, -30, -25, -14, -5, -2, 14, 14, 36, 38, 41, 42, 44, 48] >>> быстрая сортировка (get_random_numbers (10, максимум = 500)) [49, 94, 99, 124, 235, 287, 292, 333, 455, 464] >>> быстрая сортировка (get_random_numbers (10, 1000, 2000)) [1038, 1321, 1530, 1630, 1835, 1873, 1900, 1931, 1936, 1943]
Чтобы лучше понять, как работает quicksort() , см. схему ниже. Это показывает последовательность рекурсии при сортировке списка из двенадцати элементов:
схему ниже. Это показывает последовательность рекурсии при сортировке списка из двенадцати элементов:
На первом этапе значения первого, среднего и последнего списка равны 31 , 92 и 28 соответственно. Медиана 31 , так что он становится основным элементом. Тогда первый раздел состоит из следующих подсписков:
| Подсписок | Предметы |
|---|---|
[18, 3, 18, 11, 28] | Элементы меньше основного элемента |
[31] | Сам поворотный элемент |
[72, 79, 92, 44, 56, 41] | Элементы больше, чем основной элемент |
Каждый подсписок впоследствии рекурсивно разбивается таким же образом до тех пор, пока все подсписки либо не будут содержать один элемент, либо не станут пустыми. По мере возврата рекурсивных вызовов списки снова собираются в отсортированном порядке. Обратите внимание, что на предпоследнем шаге слева элемент сводки
По мере возврата рекурсивных вызовов списки снова собираются в отсортированном порядке. Обратите внимание, что на предпоследнем шаге слева элемент сводки 18 появляется в списке дважды, поэтому список элементов сводки состоит из двух элементов.
Заключение
Это завершает ваше путешествие по рекурсии , методу программирования, в котором функция вызывает сама себя. Рекурсия никоим образом не подходит для каждой задачи. Но некоторые проблемы программирования практически требуют этого. В таких ситуациях это отличная техника, которую нужно иметь в своем распоряжении.
В этом уроке вы узнали:
- Что означает, что функция вызывает сама себя рекурсивно
- Как дизайн функций Python поддерживает рекурсию
- Какие факторы следует учитывать при выборе рекурсивного решения проблемы
- Как реализовать рекурсивную функцию в Python
Вы также видели несколько примеров рекурсивных алгоритмов и сравнивали их с соответствующими нерекурсивными решениями.
Теперь вы должны быть в состоянии распознать, когда требуется рекурсия, и быть готовым уверенно использовать ее, когда это необходимо! Если вы хотите узнать больше о рекурсии в Python, ознакомьтесь с рекурсивным мышлением в Python.
Анализ рекурсии в структуре данных и алгоритмах
Рекурсия является одним из популярных подходов к решению проблем в структуре данных и алгоритмах. Даже некоторые подходы к решению задач полностью основаны на рекурсии: уменьшать и властвовать, разделять и властвовать, обход дерева и графа в DFS, поиск с возвратом, нисходящий подход динамического программирования и т. д. Таким образом, анализ сложности времени обучения рекурсии имеет решающее значение для понимания эти подходы и повысить эффективность нашего кода.
Иногда программистам сложно анализировать рекурсию из-за ее математических деталей. Но работа с рекурсивными алгоритмами становится легкой, когда мы понимаем рекурсивные шаблоны и методы, используемые в анализе. Не откладывая дальше, давайте изучим фундаментальные понятия, связанные с анализом рекурсии.
Не откладывая дальше, давайте изучим фундаментальные понятия, связанные с анализом рекурсии.
Что такое рекуррентное отношение в алгоритмах?
Рекуррентное соотношение — это уравнение, описывающее последовательность, в которой любой член определяется с использованием его предыдущих членов. Мы используем рекуррентное соотношение для анализа временной сложности рекурсивных алгоритмов с точки зрения размера входных данных.
В случае рекурсии мы решаем задачу, используя решение меньших подзадач. Если функция временной сложности алгоритма равна T(n), то временная сложность меньших подзадач будет определяться той же функцией, но с точки зрения размера входных данных подзадач.
Вот общий подход к записи T(n), если у нас есть k подзадач:
T(n) = T(входной размер 1-й подзадачи) + T(входной размер 2-й подзадачи) + …. + T(входной размер k-й подзадачи) + Временная сложность дополнительных операций, кроме рекурсивных вызовов
Приведенная выше формула обеспечивает подход к определению рекуррентного отношения каждого рекурсивного алгоритма. Затем мы решаем это рекуррентное соотношение и вычисляем общую временную сложность в терминах нотации Big-O. Давайте лучше разберемся в этом на примерах различных рекуррентных соотношений популярных рекурсивных алгоритмов.
Затем мы решаем это рекуррентное соотношение и вычисляем общую временную сложность в терминах нотации Big-O. Давайте лучше разберемся в этом на примерах различных рекуррентных соотношений популярных рекурсивных алгоритмов.
обратное (A[], l, r) - поменять местами(А[л], А[г]) - реверс(А, л + 1, г - 1) - Базовый случай: если (l >= r), то вернуть
Мы обращаем массив размера n, меняя местами первое и последнее значения и рекурсивно рекурсивно решая оставшуюся подзадачу обращения массива размера (n — 2). На каждом шаге рекурсии размер входных данных уменьшается на 2.
- Временная сложность T(n) = Временная сложность решения (n — 2) задачи размера + Временная сложность операции замены = T(n — 2) + O( 1)
- Рекуррентное соотношение для обращения массива: T(n) = T(n — 2) + c, где T(1) = c
двоичный поиск(A[], l, r, цель) - если (A[mid] == цель), вернуть середину - если (A[середина] > цель), двоичный поиск(A, l, середина - 1, цель) - if (A[mid] < target), binarySearch(A, mid + 1, r, target) Базовый случай: если (l > r), то вернуть -1
На каждом шаге рекурсии мы делаем одно сравнение и уменьшаем размер ввода вдвое. Другими словами, мы решаем задачу размера n, используя решение одной подзадачи размера входных данных n/2 (на основе сравнения, либо левой, либо правой подзадачи)
Другими словами, мы решаем задачу размера n, используя решение одной подзадачи размера входных данных n/2 (на основе сравнения, либо левой, либо правой подзадачи)
- Временная сложность T(n) = Временная сложность задачи размера n/2 + Временная сложность операции сравнения = T(n/2) + O(1).
- Рекуррентное соотношение бинарного поиска: T(n) = T(n/2) + c, где T(1) = c
сортировка слиянием (A[], l, r) - середина = l + (r - l)/2 - сортировка слиянием (А, л, середина) - сортировка слиянием (A, середина + 1, r) - слияние (А, л, середина, г) Базовый случай: если (l == r), то вернуть
При сортировке слиянием мы решаем задачу размера n, используя решение двух равных подзадач входного размера n/2 и объединяя решение подзадач за O(n) время.
- Временная сложность T(n) = Временная сложность левой подзадачи размера n/2 + Временная сложность правой подзадачи размера n/2 + Временная сложность слияния = T(n/2) + T( n/2) + O(n) = 2 T(n/2) + cn
- Рекуррентное отношение сортировки слиянием: T(n) = 2T(n/2) + cn, где T(1) = c
Быстрая сортировка (A[], l, r) - стержень = раздел (A, l, r) - быстрая сортировка (A, l, стержень - 1) - быстрая сортировка (A, точка опоры + 1, r) Базовый случай: если (l >= r), то вернуть
При быстрой сортировке мы делим массив за время O(n) и рекурсивно решаем две подзадачи разного размера. Размер подзадач зависит от выбора опорной точки в алгоритме разбиения. Предположим, что после разбиения i элементов находятся в левом подмассиве (слева от опорной точки), а n — i — 1 элементов находятся в правой подмассиве (справа от опорной точки). Размер левой подзадачи = i, Размер правой подзадачи = n — i — 1.
Размер подзадач зависит от выбора опорной точки в алгоритме разбиения. Предположим, что после разбиения i элементов находятся в левом подмассиве (слева от опорной точки), а n — i — 1 элементов находятся в правой подмассиве (справа от опорной точки). Размер левой подзадачи = i, Размер правой подзадачи = n — i — 1.
- Временная сложность T(n) = Временная сложность алгоритма разбиения + Временная сложность левой подзадачи размера i + Временная сложность правая подзадача размера (n — i — 1) = O(n) + T(i) + T(n — i — 1) = T(i) + T(n — i — 1) + cn
- Рекуррентное соотношение быстрой сортировки: T(n) = T(i) + T(n — i — 1) + cn, где T(1) = c
- Алгоритм Карацубы для быстрого умножения: Здесь мы решаем целочисленную задачу умножения размера n бит, используя три подзадачи размера n/2 бит, и объединяем эти решения. за время O(n). Рекуррентное соотношение: T(n) = 3*T(n/2) + cn, где T(1) = c
- Умножение матрицы Штрассена: 92, где Т(1) = с
fib (n) = fib (n - 1) + fib (n - 2) Базовый случай: если (n <= 1), вернуть n Здесь у нас есть 2 базовых случая: fib(0) = 0 и fib(1) = 1
. Для нахождения n-го Фибоначчи мы рекурсивно решаем и добавляем две подзадачи размера (n - 1) и (n - 2) . Обе подзадачи зависят друг от друга, поскольку значение (n-1)-го числа Фибоначчи зависит от значения (n-2)-го числа Фибоначчи и так далее. Такой тип зависимых подзадач возникает в случае задач оптимизации в динамическом программировании.
Для нахождения n-го Фибоначчи мы рекурсивно решаем и добавляем две подзадачи размера (n - 1) и (n - 2) . Обе подзадачи зависят друг от друга, поскольку значение (n-1)-го числа Фибоначчи зависит от значения (n-2)-го числа Фибоначчи и так далее. Такой тип зависимых подзадач возникает в случае задач оптимизации в динамическом программировании.
- Временная сложность T(n) = Временная сложность нахождения (n - 1)-го числа Фибоначчи + Временная сложность нахождения (n - 2)-го числа Фибоначчи + Временная сложность сложения = T(n - 1) + T(n - 2) + О(1)
- Рекуррентное соотношение для нахождения n-го числа Фибоначчи: T(n) = T(n - 1) + T(n - 2) + c, где T(n) = c для n<=1
- Сначала мы определяем размер входных данных для более крупной задачи.
- Затем мы узнаем общее количество меньших подзадач.

- Наконец, мы определяем входной размер меньших подзадач.
- Мы определяем функцию временной сложности для более крупной задачи с точки зрения размера входных данных. Например, если размер входных данных равен n, то функция временной сложности будет T(n).
- Затем мы определяем временную сложность меньших подзадач. Например, в случае сортировки слиянием входной размер обеих подзадач равен n/2 каждая, поэтому временная сложность каждой подзадачи будет T(n/2).
- Теперь мы анализируем временную сложность дополнительных операций в наихудшем случае. Например, в сортировке слиянием деление (O(1)) и процесс слияния (O(n)) являются дополнительными операциями, которые нам нужно выполнить, чтобы получить больший отсортированный массив.
- Мы добавляем временные сложности подзадач и дополнительные операции, чтобы получить уравнение общей функции временной сложности T(n).

- Мы также определяем временную сложность базового случая, т. е. наименьшую версию задачи. Наше решение рекуррентности зависит от этого, поэтому нам нужно правильно определить его. Считать!
В основном мы используем следующие два метода для решения рекуррентных соотношений в алгоритмах и структуре данных. Мы можем выбирать эти методы в зависимости от характера рекуррентного соотношения. Основной метод лучше всего подходит для анализа задач типа «разделяй и властвуй», но метод дерева рекурсии всегда является фундаментальным подходом, применяемым ко всем типам рекурсивных алгоритмов.
- Метод 1 : Метод дерева рекурсии
- Метод 2 : Основная теорема
Метод 1: метод дерева рекурсии
Дерево рекурсии — это древовидная диаграмма рекурсивных вызовов, где каждый узел дерева представляет стоимость определенной подзадачи. Идея была бы проста! Временная сложность рекурсии зависит от двух факторов: 1) общего количества рекурсивных вызовов и 2) временной сложности дополнительных операций для каждого рекурсивного вызова.
Идея была бы проста! Временная сложность рекурсии зависит от двух факторов: 1) общего количества рекурсивных вызовов и 2) временной сложности дополнительных операций для каждого рекурсивного вызова.
Таким образом, дерево рекурсии представляет собой диаграмму, показывающую дополнительные затраты на каждый рекурсивный вызов с точки зрения размера входных данных. Мы должны добавить дополнительную стоимость для каждого рекурсивного вызова, чтобы получить общую временную сложность. Примечание. Одной из лучших идей было бы выполнять эту сумму затрат по уровням.
Шаги анализа с использованием метода дерева рекурсии- Нарисовать дерево рекурсии заданного рекуррентного отношения
- Подсчитать общее количество уровней в дереве рекурсии.
- Рассчитайте стоимость дополнительных операций на каждом уровне, добавив стоимость каждого узла, присутствующего на том же уровне.
- Наконец, добавьте стоимость каждого уровня, чтобы определить общую стоимость рекурсии.
 Мы упрощаем это выражение и находим общую временную сложность в терминах большой нотации O.
Мы упрощаем это выражение и находим общую временную сложность в терминах большой нотации O.
Рекуррентное соотношение сортировки слиянием: T(n) = 2T(n/2) + cn, T(1) = c на два разных подмассива (подзадачи) размера n/2. Здесь cn представляет собой стоимость слияния решения меньших подзадач (меньших отсортированных массивов размера n/2). Таким образом, на каждом шаге рекурсии задача будет делиться пополам, пока размер подзадачи не станет равным 1.
- Начнем с термина cn в качестве корня, что является стоимостью дополнительных операций на первом уровне дерева рекурсии. Левый и правый дочерние элементы корня представляют собой временную сложность двух меньших подзадач, то есть T (n/2).
- Теперь мы продвинемся на один уровень дальше, расширив T(n/2).
- На втором уровне есть два узла и стоимость дополнительных операций в каждом узле cn/2.
 Таким образом, общая стоимость дополнительных операций на втором уровне рекурсии = cn/2 + cn/2 = cn 9и) =сп.
Таким образом, общая стоимость дополнительных операций на втором уровне рекурсии = cn/2 + cn/2 = cn 9и) =сп.
Здесь дерево рекурсии — это полная двоичная древовидная структура, в которой каждый узел имеет двух дочерних элементов, а каждый уровень полностью заполнен. На каждом уровне размер входных данных уменьшается в 2 раза, и дерево рекурсии завершится при размере входных данных 1. Таким образом, высота дерева рекурсии h = logn (подумайте!)
- Общее количество уровней в двоичном дереве = высота бинарного дерева + 1 = logn + 1
- Чтобы вычислить общую стоимость повторения, мы суммируем стоимость всех уровней. Дерево рекурсии имеет logn + 1 уровней, каждый из которых стоит cn. Таким образом, общая стоимость = cn * (logn + 1) = cnlogn + cn
- После игнорирования младшего члена и константы c в (cnlogn + cn) временная сложность сортировки слиянием = O(nlogn)
Для дальнейшего изучения изучите анализ бинарного поиска и быстрой сортировки с использованием метода рекурсивного дерева. k), где a≥1 и b>1. 9k) в большинстве задач кодирования.
k), где a≥1 и b>1. 9k) в большинстве задач кодирования.
Сравнение отношения основной теоремы с рекуррентным отношением бинарного поиска: 92.8)
Изучение анализа следующих рекурсивных алгоритмов
- Рекурсивный поиск максимального элемента в массиве: T(n) = T(n - 1) + O(1)
- Рекурсивная сортировка вставками: T(n) = T(n - 1) + O(n) Головоломка
- Ханойская башня: T(n) = 2T(n - 1) + O(1)
- Поиск ближайшей пары точек: T(n) = 2T(n/2) + O(nlogn)
- Алгоритм «разделяй и властвуй» нахождения максимума и минимума: T(n) = 2T(n/2) + O(1)
- Алгоритм «разделяй и властвуй» для максимальной суммы подмассивов: T(n) = 2T(n/2) + O(n)
- Рекурсивный поиск в сбалансированном BST: T(n) = T(n/2) + O(1)
- Обход бинарного дерева в DFS: T(n) = T(i) + T(n - i - 1) + O(1), где i узлов находится в левом поддереве и (n - i - 1) количество узлов в правом поддереве
- Анализ среднего случая алгоритма быстрого выбора для нахождения k-го наименьшего элемента: T(n) = 2/n (i = n/2 to n-1 ∑ T(i)) + cn
- Рекурсивный алгоритм грубой силы самой длинной общей подпоследовательности: T(n, m) = T(n-1, m-1) + O(1), если последние значения строк равны, иначе T(n, m) = Т(n-1, m) + T(n, m-1) + O(1)
Наслаждайтесь обучением, Наслаждайтесь программированием, Наслаждайтесь алгоритмами!
Анализ и корректность простых рекурсивных алгоритмов
SI335: Анализ и корректность простых рекурсивных алгоритмовЧтение
Эти заметки.
Домашнее задание
Домашнее заданиеРекурсивная версия percolateMax
Вот рекурсивный вариант алгоритма percolate max из последнее домашнее задание.
Алгоритм: percolateMax(A,i,j)
Ввод: A,i,j - где A - массив целых чисел, i..j диапазон в A
Вывод: z - максимальный элемент среди A[i..j]
Дополнительное условие: элементы A[i..j] переупорядочены s.t. г = А [j]
если я < j
percolateMax(A,i,j-1)
если А[j] < А[j-1]
своп(А[j-1],А[j])
возврат А[j]
Доказательство правильности: Для доказательства рекурсивного алгоритма
правильно, мы должны (снова) провести индуктивное доказательство. Это может быть
тонкий, потому что мы индуцируем "на" что-то. Другими словами,
должна быть некоторая неотрицательная целая величина, связанная
на вход, который становится меньше с каждым рекурсивным вызовом, пока
мы в конечном итоге попали в базовый случай. Для percolateMax мы будем
индукция по количеству элементов в диапазоне i..j. Итак, мы будем
доказать, что алгоритм соответствует спецификации для базы
случае (т.е. когда в i..j есть только один элемент), и тогда мы
докажет, что он удовлетворяет своей спецификации при наличии $n$
элементы в диапазоне i..j, предполагая (по индукции), что
соответствует своей спецификации всякий раз, когда он вызывается на меньших диапазонах.
Для percolateMax мы будем
индукция по количеству элементов в диапазоне i..j. Итак, мы будем
доказать, что алгоритм соответствует спецификации для базы
случае (т.е. когда в i..j есть только один элемент), и тогда мы
докажет, что он удовлетворяет своей спецификации при наличии $n$
элементы в диапазоне i..j, предполагая (по индукции), что
соответствует своей спецификации всякий раз, когда он вызывается на меньших диапазонах.
Примечание: Вы могли заметить, что «Дополнительное условие» я добавил согласно спецификации алгоритма, по сути, это цикл инвариант, который вы придумали в домашнем задании для итеративного версия. Это не должно быть сюрпризом.
Анализ времени выполнения: Предположим, я хочу проанализировать наихудшее время работы
percolateMax через $n$, количество элементов в i..j,
назовите это $T_w(n)$. Поскольку алгоритм рекурсивный, я могу
определить $T_w(n)$ только в терминах самого себя. Так что я заканчиваю с
что-то типа
\[
T_w(n) \leq T_w(n-1) + O(1)
\]
т.е. рекуррентное отношение . Таким образом, для всех $n \gt 1$
существует достаточно большая положительная постоянная такая, что
$T_n(1) \leq c$ и
\[
T_w(n) \leq T_w(n-1) + c
\]
Расширение этого дает $T_w(n) \leq c n$, поэтому
$T_w(n) \in O(n)$
Так что я заканчиваю с
что-то типа
\[
T_w(n) \leq T_w(n-1) + O(1)
\]
т.е. рекуррентное отношение . Таким образом, для всех $n \gt 1$
существует достаточно большая положительная постоянная такая, что
$T_n(1) \leq c$ и
\[
T_w(n) \leq T_w(n-1) + c
\]
Расширение этого дает $T_w(n) \leq c n$, поэтому
$T_w(n) \in O(n)$
Рекурсивная версия алгоритма uniqueDest
Вспомните алгоритм uniqueDest из предыдущее домашнее задание. Вот рекурсивная версия этого алгоритма.
Алгоритм: uniqueDest(P,n,s)
Входы: P,n,s --- входной экземпляр Уникальный пункт назначения проблема
Вывод: TRUE/FALSE решение проблемы Unique Destination
следующий = количество = я = 0
в то время как i < n do ← этот цикл подсчитывает количество дочерних элементов s и устанавливает рядом с последним увиденным дочерним элементом
если P[i] == s
количество = количество + 1
следующий = я
я = я + 1
если количество == 1
вернуть uniqueDest (P, n, следующий)
еще
количество возвратов == 0
Подтверждение правильности: Как и раньше, мы доказываем правильность этого рекурсивного алгоритма, используя
индуктивное доказательство. Но на что делать индукцию? Нам надо
найти что-то, что получает
меньше с каждым рекурсивным вызовом, но что? $P$ и $n$ остаются
то же самое с каждым рекурсивным вызовом, так что не те. Как насчет
$с$? Это не обязательно становится меньше. Если я смотрю на
$s = 7$ это просто означает, что я нахожусь в вершине 7, а индекс
дочерний узел может быть любым: он может быть больше, он может быть
меньше. Так что это не работает. Итак, что мы можем
индукция включена?
Но на что делать индукцию? Нам надо
найти что-то, что получает
меньше с каждым рекурсивным вызовом, но что? $P$ и $n$ остаются
то же самое с каждым рекурсивным вызовом, так что не те. Как насчет
$с$? Это не обязательно становится меньше. Если я смотрю на
$s = 7$ это просто означает, что я нахожусь в вершине 7, а индекс
дочерний узел может быть любым: он может быть больше, он может быть
меньше. Так что это не работает. Итак, что мы можем
индукция включена?
На самом деле, это то, что я должен знать, потому что в рекурсивный алгоритм, мне нужно убедиться, что я «работаю над базовый случай» при каждом рекурсивном вызове. И снова я должен приближается к базовому случаю, поэтому что-то должно быть становится меньше. Что это? Один естественный выбор: длина самого длинного пути, начинающегося с $s$ . Назовем это $d_s$. Поскольку у нас есть лес, если $c$ равно дочерний элемент $s$, затем $d_s \geq 1 + d_c$.
Итак, мы докажем, что uniqueDest соответствует своей спецификации, используя
индукция по $d_s$.
- Базовый вариант: Если $d_s = 0$, мы возвращаем true, что правильно, поскольку $s$ лист, что означает, что это его собственное уникальное предназначение.
- Индуктивный корпус: Если $d_s \gt 0$, то цикл устанавливает
countв количество детей $s$, иследующихдо один из детей $s$. Обратите внимание, что $s$ имеет дочерние элементы в этом случае, поскольку $d_s \gt 0$. Еслисчитать$\gt 1$, алгоритм возвращает false, что верно, поскольку $s$ имеет несколько дочерних элементов и, следовательно, не имеет уникального назначения. В противном случаеследующий— уникальный дочерний элемент, а $s$ имеет уникальное назначение тогда и только тогда, когда это уникальное ребенокследующийимеет уникальное назначение. С $d_{\text{next}} \lt d_s$, мы можем сказать, индукция, что вызовuniqueDest(P,n,next)соответствует спецификации, и, таким образом, возвращая этот результат получаем правильный ответ.
Анализ времени выполнения: Здесь мы можем ошибочно записать рекуррентное соотношение
\[
T_w(n) \leq T_w(n-1) + O(n)
\]
чтобы выразить время работы в наихудшем случае,
но это на самом деле неправильно! Почему?
Потому что при рекурсивных вызовах $n$ не становится меньше.
Если мы используем $d$ для представления длины самого длинного пути из
$s$, то правильное рекуррентное соотношение
\[
T_w(d) \leq T_w(d-1) + O(n)
\]
для любого $d \gt 0$.
Таким образом, для некоторой достаточно большой константы $c$ получаем
\[
T_w(d) \leq T_w(d-1) + cn
\]
для любого $d \gt 0$.
Теперь, если вы расширите это, мы получим
\[
T_w(d) \leq c d n.
\]
Когда мы видим, что это написано таким образом, мы понимаем, что
время работы в худшем случае на самом деле является функцией двух
параметры: $d$ и $n$. Итак, мы действительно должны написать:
\[
T_w(n,d) \in O(dn)
\]
Мы могли бы оставить все как есть, и у нас был бы правильный
отвечать. С другой стороны, мы часто хотим, чтобы наша работа
время только с точки зрения размера ввода ($n$ в этом
случай), а не с точки зрения других свойств. 2)$.
2)$.
Рекурсивные алгоритмы для оценки параметров в режиме онлайн - MATLAB & Simulink
Рекурсивные алгоритмы для оценки параметров в режиме онлайн
Алгоритмы рекурсивной оценки в System Identification Toolbox™ можно разделить на две категории:
Алгоритмы с бесконечной историей — Эти алгоритмы направлены на минимизацию ошибки между наблюдаемыми и прогнозируемыми выходными данными для всех временных шагов от начало симуляции. System Identification Toolbox поддерживает оценку бесконечной истории в:
Рекурсивные оценщики командной строки для линейного метода наименьших квадратов регрессия, модель AR, ARX, ARMA, ARMAX, OE и BJ структуры
Simulink ® Рекурсивная оценка методом наименьших квадратов и Оценщик рекурсивной полиномиальной модели блоки
Алгоритмы с конечной историей.
 Эти алгоритмы направлены на минимизацию ошибки.
между наблюдаемыми и прогнозируемыми выходными данными за конечное число прошедших периодов времени
шаги. Набор инструментов поддерживает оценку с конечной историей для
линейные по параметрам модели:
Эти алгоритмы направлены на минимизацию ошибки.
между наблюдаемыми и прогнозируемыми выходными данными за конечное число прошедших периодов времени
шаги. Набор инструментов поддерживает оценку с конечной историей для
линейные по параметрам модели:Рекурсивные оценщики командной строки для линейного метода наименьших квадратов структуры моделей регрессии, AR, ARX и OE
Симулинк Блок рекурсивной оценки методом наименьших квадратов
Simulink Блок Recursive Polynomial Model Estimator, для Только конструкции AR, ARX и OE
Алгоритмы с конечной историей обычно легче настроить, чем алгоритмы с бесконечной историей, когда параметры имеют быстрые и потенциально большие колебания во времени.
 9(t|θ) по параметрам θ.
9(t|θ) по параметрам θ.Самый простой способ наглядно представить роль градиента ψ(t) параметров — рассмотреть модели с форма линейной регрессии:
y(t)=ψT(t)θ0(t)+e(t)
В этом уравнении ψ(t) представляет собой вектор регрессии , который вычисляется на основе предыдущих значений измеренных входов и выходов. θ0(t) представляет истинные параметры. е(т) есть источник шума ( 9(t−1) для общих структур модели см. раздел о рекурсивных методы предсказания ошибки в [1].
Типы алгоритмов рекурсивной оценки с бесконечной историей
Программное обеспечение System Identification Toolbox предоставляет следующие рекурсивные алгоритмы с бесконечной историей алгоритмы оценки для онлайн-оценки:
Фактор забывания
Фильтр Калмана
Нормализованный и ненормализованный градиент
Формулировки коэффициента забывания и фильтра Калмана более вычислительны.
 интенсивнее, чем градиентный и ненормированный градиентный методы. Однако они
обычно имеют лучшие свойства сходимости.
интенсивнее, чем градиентный и ненормированный градиентный методы. Однако они
обычно имеют лучшие свойства сходимости.Фактор забывания. Следующий набор уравнений резюмирует забывание фактор 9(t−1)
K(t)=Q(t)ψ(t)
Q(t)=P(t−1)λ+ψT(t)P(t−1)ψ(t)
P(t)=1λ(P(t−1)−P(t−1)ψ(t)ψ(t)TP(t−1)λ+ψ(t)TP(t−1)ψ(t ))
Программное обеспечение гарантирует, что P(t) является положительно определенной матрицей с помощью алгоритма извлечения квадратного корня для его обновления [2]. Программное обеспечение вычисляет
P, предполагая, что остатки (разница между расчетными и измеренными выходными данными) представляют собой белый шум, а дисперсия этих остатков равна 1. 9(k))2Подробнее см. раздел 11.2 в [1].
Этот подход дисконтирует старые измерения экспоненциально, так что наблюдение, имеющее возраст τ выборок, имеет вес, равный λτ, умноженному на вес самого последнего наблюдения.
 τ=11−λ представляет горизонт памяти этого
алгоритм. Измерения старше τ=11−λ обычно имеют вес меньше примерно 0,3.
τ=11−λ представляет горизонт памяти этого
алгоритм. Измерения старше τ=11−λ обычно имеют вес меньше примерно 0,3.λ называется фактором забывания и обычно имеет положительное значение между 9(t−1)
K(t)=Q(t)ψ(t)
Q(t)=P(t−1)R2+ψT(t)P(t−1)ψ(t)
P(t)=P(t−1)+R1−P(t−1)ψ(t)ψ(t)TP(t−1)R2+ψ(t)TP(t−1)ψ(t )
Программное обеспечение гарантирует, что P(t) является положительно определенной матрицей с помощью алгоритма извлечения квадратного корня для его обновления [2]. Программное обеспечение вычисляет
P, предполагая, что остатки (разница между расчетными и измеренными выходными данными) представляют собой белый шум, а дисперсия этих остатков равна 1. Р 2 *Ресть ковариационная матрица оцениваемых параметров, и Р 1 / R 2 — ковариация матрица изменения параметра. Где, R 1 — ковариационная матрица
изменения параметров, которые вы укажете.
Где, R 1 — ковариационная матрица
изменения параметров, которые вы укажете.Эта формулировка предполагает форму линейной регрессии модели:
y(t)=ψT(t)θ0(t)+e(t)
Q(t) вычисляется с использованием фильтра Калмана.
Эта формулировка также предполагает, что истинные параметры θ0(t) описываются случайным блужданием: шум со следующим ковариационная матрица или дрейфовая матрица R 1 :
Ew(t)wT(t)=R1
R 2 - это дисперсия инновации e(t) в следующем уравнении:
y(t)=ψT(t)θ0(t)+e(t)
Алгоритм фильтра Калмана полностью определяется последовательностью данных y(t) , градиент ψ(t), R 1 , R 2 , а начальный условия θ(t=0) (начальное предположение параметров) и P(t=0) (ковариационная матрица, указывающая параметры ошибки).
 9(t−1)
9(t−1)K(t)=Q(t)ψ(t)
В методе ненормированного градиента Q(t) дается по:
Q(t)=γ
В методе нормализованного градиента Q(t) дается by:
Q(t)=γ|ψ(t)|2+Bias
Алгоритм нормализованного градиента масштабирует усиление адаптации, γ , на каждом шаге квадратом 2-нормы вектор градиента. Если градиент близок к нулю, это может вызвать скачки в предполагаемые параметры. Чтобы предотвратить эти скачки, вводится член смещения в коэффициенте масштабирования. 9(k|θ) — прогнозируемый результат в момент времени k . Этот подход также известен как оценка скользящего окна. Оценка конечной истории подходы минимизируют ошибки предсказания для последних N временных шагов. Напротив, методы оценки с бесконечной историей минимизируют ошибки прогнозирования, начиная с с начала симуляции.
 (k|θ)=Ψ(k)θ(k−1). Программное обеспечение создает и поддерживает буфер регрессоров. ψ ( k ) и наблюдаемые результаты y ( k ) for k = t - N +1, т - с.ш. +2, … , т -2, т -1, т . Эти буферы содержат необходимые матрицы для базовой
задача линейной регрессии минимизации ‖Ψbufferθ−ybuffer‖22 по θ . Программное обеспечение решает эту линейную
проблема регрессии с использованием QR-факторинга с поворотом столбца.
(k|θ)=Ψ(k)θ(k−1). Программное обеспечение создает и поддерживает буфер регрессоров. ψ ( k ) и наблюдаемые результаты y ( k ) for k = t - N +1, т - с.ш. +2, … , т -2, т -1, т . Эти буферы содержат необходимые матрицы для базовой
задача линейной регрессии минимизации ‖Ψbufferθ−ybuffer‖22 по θ . Программное обеспечение решает эту линейную
проблема регрессии с использованием QR-факторинга с поворотом столбца.Ссылки
[1] Ljung, L. System Identification: Theory for the Пользователь . Река Аппер-Сэдл, Нью-Джерси: Prentice-Hall PTR, 1999.
[2] Карлсон, Н. А. «Быстрая треугольная формулировка квадрата корневой фильтр». Журнал AIAA , том 11, номер 9, 1973, стр.
 1259-1265 гг.
1259-1265 гг.[3] Чжан, В. "Некоторые Аспекты реализации алгоритмов наименьших квадратов со скользящим окном». IFAC Труды . Том. 33, выпуск 15, 2000, стр. 763-768.
См. также
Рекурсивный метод наименьших квадратов | Оценщик рекурсивной полиномиальной модели |
рекурсивныйAR|рекурсивныйARMA|рекурсивныйARX|рекурсивныйARMAX|рекурсивныйOE|рекурсивныйBJ|рекурсивныйLSСвязанные темы
- Что такое онлайн-оценка?
Рекурсивный алгоритм. - Решение всех больших проблем заключается в… | от Пушпи Карн
- Решение всех больших проблем лежит в более мелких проблемахПроблема с цифровой архитектурой заключается в том, что алгоритм может создавать бесконечные варианты, поэтому у архитектора есть много вариантов.

-Peter Eisenman
Прежде чем углубляться в технические термины, давайте разберемся с рекурсией на простом примере. Вы когда-нибудь видели русскую куклу? Что происходит, когда мы снимаем верхнюю половину куклы, мы видим внутри нее куклу чуть меньшего размера. Опять же, сняв куклу и отделив ее верхушку, мы видим внутри нее еще одну куклу и так продолжается до тех пор, пока не появится самая маленькая кукла.
На этой картинке видно, как одна большая матрешка была разделена на более мелкие.Основная идея рекурсии та же , чтобы решить проблему, решив меньшую проблему того же самого, если только проблема не настолько мала, что мы можем просто решить ее напрямую.
Процесс, в котором функция прямо или косвенно вызывает саму себя, называется рекурсией, а сама функция называется рекурсивной функцией.
Давайте поймем то же самое математически,
Предположим, вы хотите найти сумму первых n натуральных чисел, вы можете найти ее либо с помощью
- Простое добавление чисел от 1 до n, что будет выглядеть как
2.
Подход 2 Мы могли бы просто следовать рекурсивному методу, т.е. инициализировать функцию f(n)=1, где n=1, и добавить f( n-1) на n для каждого n>1
Мы могли бы просто следовать рекурсивному методу, т.е. инициализировать функцию f(n)=1, где n=1, и добавить f( n-1) на n для каждого n>1Во втором методе функция вызывает себя внутри функции, и это явление называется рекурсией.
Используя рекурсивные алгоритмы, некоторые сложные задачи могут быть решены довольно легко. Например, обход деревьев, Ханойская башня и т. д.
И рекурсивная, и итерационная программы обладают одинаковыми способностями к решению задач, т. е. рекурсивная функция может быть записана как итерационная программа, и наоборот. На первый взгляд и рекурсия, и итерация могут выглядеть одинаково, но они сильно отличаются друг от друга.
Рекурсия — это процесс, который всегда применяется к функции, он многократно вызывает сам себя. Принимая во внимание, что итерация происходит, когда цикл выполняется до тех пор, пока условие не станет ложным, и оно применяется к набору инструкций. С другой стороны, рекурсия завершается, когда распознан базовый случай.
 Рекурсия более эффективна, чем итерация.
Рекурсия более эффективна, чем итерация.Код для рекурсии :
Код рекурсииВывод: Фактор 5 IS 120
Код для итерации:
Код итерации. определить базовое состояние. Как упоминалось в предыдущем подразделе, рекурсия завершается, когда распознается базовый вариант. Исходя из базового случая, мы имеем в виду, что решение базового случая предоставляется, а решение большей проблемы выражается в терминах меньших проблем.
Каждая рекурсивная программа должна иметь базовый случай, чтобы гарантировать, что функция завершится в какой-то момент. Отсутствие базового случая приведет к неожиданному поведению.
Существуют определенные свойства рекурсивных алгоритмов, а именно
1. Базовые критерии - Должен быть хотя бы один базовый критерий, чтобы функция не переходила в бесконечное состояние.
2. Прогрессивный подход. Функции должны вызываться таким образом, чтобы базовый вариант был ближе, чтобы можно было найти окончательный ответ.

В этом примере определен базовый вариант n<=1, и для каждой более крупной проблемы, которая будет оцениваться, сначала будет решаться этот базовый вариант.
Каковы три закона рекурсии?
Все рекурсивные алгоритмы должны следовать этим трем очень важным правилам, чтобы они могли работать должным образом1. Этот алгоритм должен вызывать себя рекурсивно
2. Он должен иметь базовый случай
3. Алгоритм должен двигаться в сторону базового случая.
Большинство языков программирования реализуют рекурсию с использованием стеков. Основная идея состоит в том, чтобы представить проблему в виде более мелких задач и продолжать решать ее до тех пор, пока не будет достигнуто базовое условие. Например, при вычислении факториала n нам нужно знать значение факториала (n-1), и для этого базовым условием будет n=0, которое вернет 1 (как 0!=1 )
В приведенном выше примере n=4 нам нужно найти значение факториала 4, для которого определена функция fact.
 Чтобы вычислить то же самое, должно быть известно значение fact(3) и так далее. Таким образом, мы достигаем базового случая, который является фактом (0) = 1, который уже определен. С помощью этого мы вычисляем значение факта (1) до факта (4).
Чтобы вычислить то же самое, должно быть известно значение fact(3) и так далее. Таким образом, мы достигаем базового случая, который является фактом (0) = 1, который уже определен. С помощью этого мы вычисляем значение факта (1) до факта (4).Для нахождения временной сложности в рекурсии мы подсчитываем, сколько раз выполняется рекурсивный вызов. Вызов функции равен O(1), поэтому (n) количество раз, когда рекурсивный вызов выполняется, делает рекурсивную функцию O(n).
Объем дополнительного пространства, необходимого для выполнения модуля, зависит от его пространственной сложности. При рекурсии система должна сохранять запись активации каждый раз, когда выполняется рекурсивный вызов. Отсюда считается, что объемная сложность рекурсии выше, чем итерации.
Рекурсия использует стековую память. Когда какая-либо функция вызывается из основной функции, она выделяется ей в стеке. Поскольку рекурсивная функция вызывает сама себя, память для вызываемой функции выделяется поверх памяти, выделенной вызывающей функции, и для каждого вызова функции создается другая копия локальных переменных.


 При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.
 (например, треугольник Серпинского).
(например, треугольник Серпинского).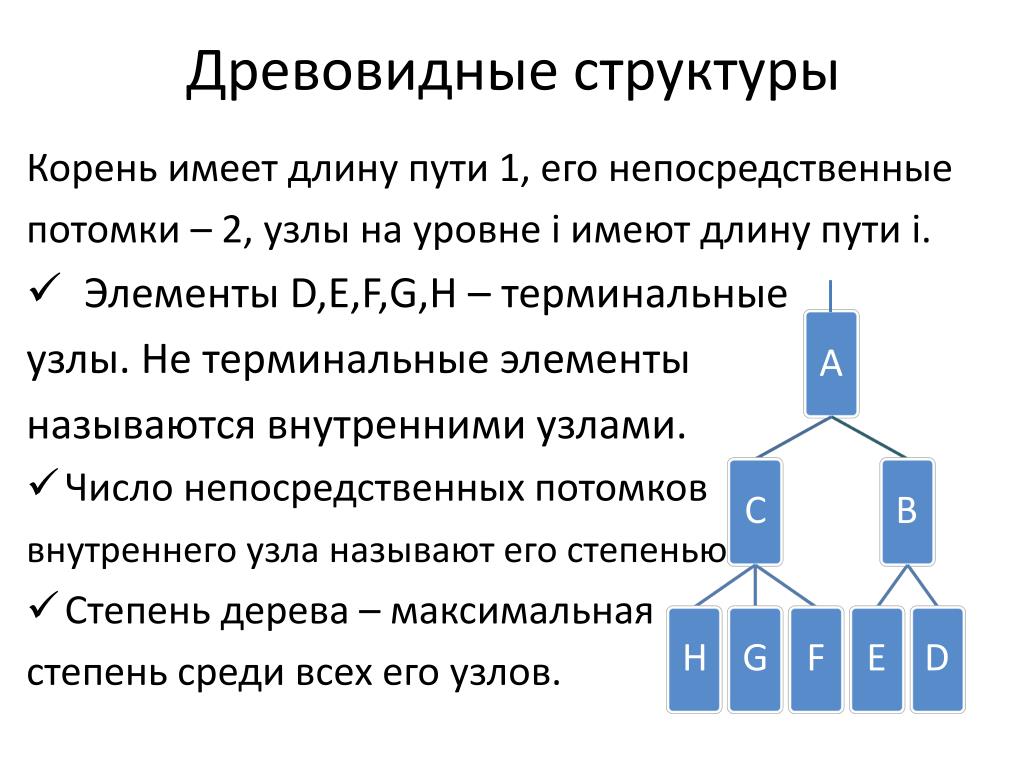 рекурсия
рекурсия (например, треугольник Серпинского).
(например, треугольник Серпинского). рекурсия
рекурсия (например, треугольник Серпинского).
(например, треугольник Серпинского).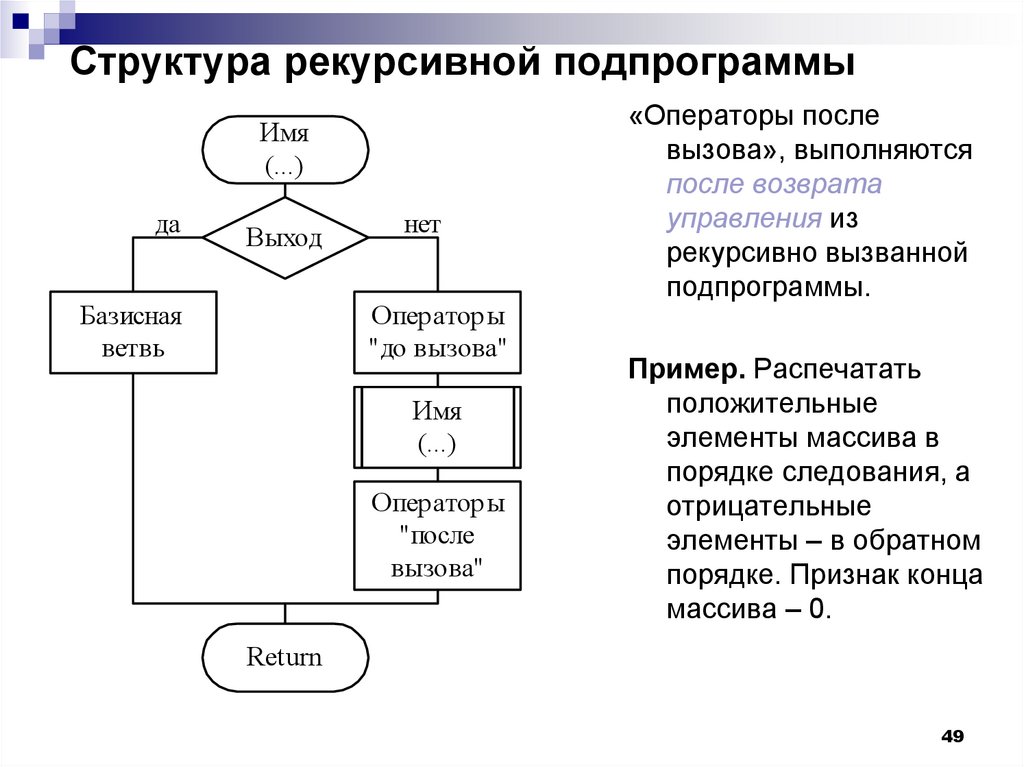 рекурсия
рекурсия

 ..
>>> факториал(4)
factorial() вызывается с n = 4
factorial() вызывается с n = 3
factorial() вызывается с n = 2
factorial() вызывается с n = 1
-> факториал(1) возвращает 1
-> факториал(2) возвращает 2
-> факториал(3) возвращает 6
-> факториал(4) возвращает 24
24
..
>>> факториал(4)
factorial() вызывается с n = 4
factorial() вызывается с n = 3
factorial() вызывается с n = 2
factorial() вызывается с n = 1
-> факториал(1) возвращает 1
-> факториал(2) возвращает 2
-> факториал(3) возвращает 6
-> факториал(4) возвращает 24
24
 .. возвращаемое_значение = 1
... для i в диапазоне (2, n + 1):
... возвращаемое_значение *= я
... вернуть возвращаемое_значение
...
>>> факториал(4)
24
.. возвращаемое_значение = 1
... для i в диапазоне (2, n + 1):
... возвращаемое_значение *= я
... вернуть возвращаемое_значение
...
>>> факториал(4)
24
 .. print("Итеративно:")
... факториал по умолчанию (n):
... возвращаемое_значение = 1
... для i в диапазоне (2, n + 1):
... возвращаемое_значение *= я
... вернуть возвращаемое_значение
... """
>>> из timeit импортировать timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Итеративный:
3.733752099999947
.. print("Итеративно:")
... факториал по умолчанию (n):
... возвращаемое_значение = 1
... для i в диапазоне (2, n + 1):
... возвращаемое_значение *= я
... вернуть возвращаемое_значение
... """
>>> из timeit импортировать timeit
>>> timeit("factorial(4)", setup=setup_string, number=10000000)
Итеративный:
3.733752099999947
 1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(имена)
10
>>> # Успех!
1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(имена)
10
>>> # Успех!
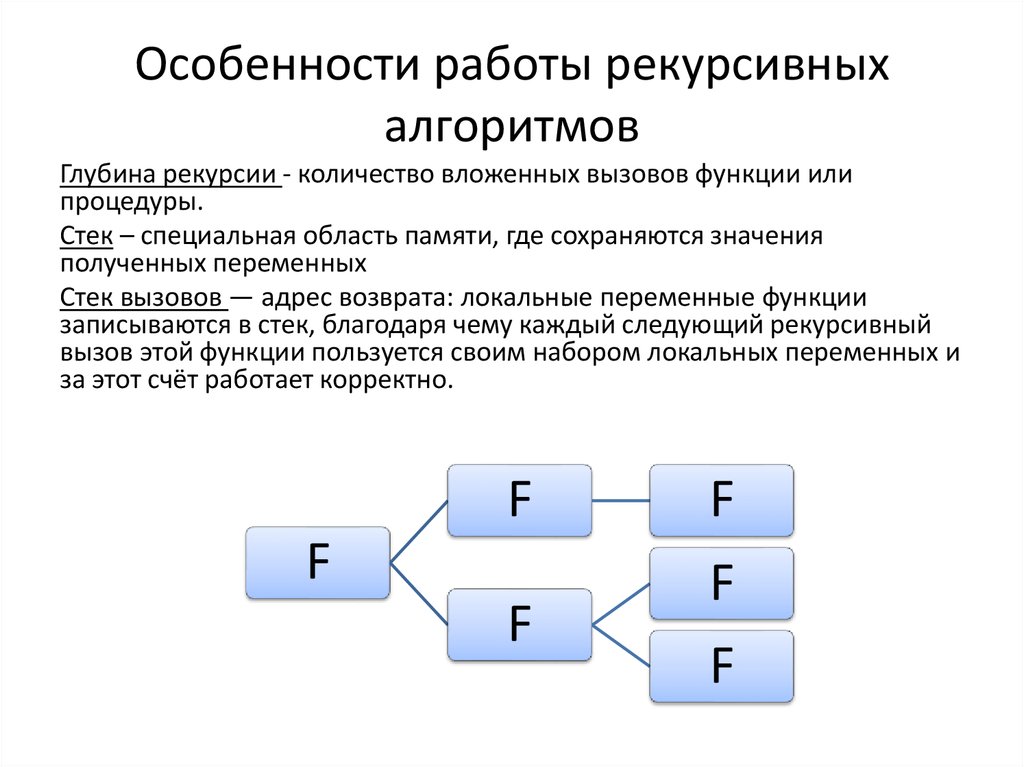
 1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(имена)
10
>>> # Успех!
1, 2.2], 3])
4
>>> count_leaf_items([])
0
>>> count_leaf_items(имена)
10
>>> # Успех!

