Рекурсия в алгоритме будет прямой когда: НОУ ИНТУИТ | Лекция | Рекурсия и рекурсивные алгоритмы

Тест: Теория алгоритмов №3 — Информатика 11 класс

Тест: Теория алгоритмов №3 — Информатика 11 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP — доступ

• Предметы
»
• Информатика
»
• 11 класс
»
• Теория алгоритмов №3

Теория алгоритмов №3

Информатика 11 класс | Автор: Гайнанова Эльвина Назимовна | ID: 9292 | Дата: 21.3.2017

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Вопрос № 1

Рекурсия в алгоритме будет прямой, когда:

рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;
порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.

Вопрос № 2

Рекурсия в алгоритме будет косвенной, когда:

рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;

порядок следования команд определяется в зависимости от результатов проверки некоторых условий;
команда обращения алгоритма к самому себе находится в самом алгоритме;
один вызов алгоритма прямо следует за другим.

Вопрос № 3

Команда машины Поста имеет структуру п Km, где:

n — действие, выполняемое головкой; К — номер следующей команды, подлежащей выполнению; m — порядковый номер команды;
n — порядковый номер команды; К — действие, выполняемое головкой; m — номер следующей команды, подлежащей выполнению;

n — порядковый номер команды; К — номер следующей команды, подлежащей выполнению; m — действие, выполняемое головкой;
n — порядковый номер команды; К- действие, выполняемое головкой; m — номер клетки, с которой данную команду надо произвести.

Вопрос № 4

Сколько существует команд у машины Поста:

2
4
6
8

Вопрос № 5

В машине Поста останов будет результативным:

при выполнении недопустимой команды;
если машина не останавливается никогда;
если результат выполнения программы такой, какой и ожидался;
по команде «Стоп».

Вопрос № 6

В машине Поста некорректным алгоритм будет в следующем случае:

при выполнении недопустимой команды;
результат выполнения программы такой, какой и ожидался;
машина не останавливается никогда;
по команде «Стоп».

Вопрос № 7

В машине Тьюринга предписание L для лентопротяжного механизма означает:

переместить ленту вправо;
переместить ленту влево;
остановить машину;
занести в ячейку символ.

Вопрос № 8

В машине Тьюринга предписание R для лентопротяжного механизма означает:

переместить ленту вправо;
переместить ленту влево;
остановить машину;
занести в ячейку символ.

Вопрос № 9

В машине Тьюринга предписание S для лентопротяжного механизма означает:

переместить ленту вправо;
переместить ленту влево;
остановить машину;
занести в ячейку символ.

Вопрос № 10

В алгоритме Маркова ассоциативным исчислением называется:

совокупность всех слов в данном алфавите;
совокупность всех допустимых систем подстановок;
совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;
когда все слова в алфавите являются смежными.

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu.ru 2013-2022

E-mail администратора: [email protected]

Теория алгоритмов, Прямой анализ рекурсивного дерева вызовов

Алгоритм сортировки слиянием

Рассмотрим подход к получению функции трудоемкости рекурсивного алгоритма, основанный на непосредственном подсчете вершин дерева рекурсивных вызовов, на примере алгоритма сортировки слиянием.

Рекурсивная процедура Merge Sort – MS получает на вход массив А и два индекса p и q, указывающие на ту часть массива, которая будет сортироваться при данном вызове. Вспомогательные массивы Bp и Bq используются для слияния отсортированных частей массива.

MS(A, p ,q, Bp, Bq)
If pq (проверка останов рекурсии при p=q)
then
r MS(A, p, r, Bp,Bq) (рекурсивный вызов для первой части)
MS(A, r+1, q, Bp,Bq) (рекурсивный вызов для второй части)
Merge(A, p, r, q, Bp, Bq) (слияние отсортированных частей)
Return (A)
End

Слияние отсортированных частей (Merge)

Рассмотрим процедуру слияния отсортированных частей массива А, использующую дополнительные массивы Bp и Bq, в конец которых с целью остановки движения индекса помещается максимальное значение.

Поскольку сам алгоритм рекурсивной сортировки устроен так, что объединяемые части массива А находятся рядом друг с другом, то алгоритм слияния вначале копирует отсортированные части в промежуточные массивы, а затем формирует объединенный массив непосредственно в массиве А.

Merge (A,p,r,q,Bp,Bq) (В {} взято количество операций в данной строке)

Max If Max Max kp p1 For i Bp [ i ] Bp[ kp+1] kq For i Bq [ i ] Bq [ kq+ 1] (заметим, что m=kp + kq = q – p + 1 – длина объединенного массива)
pp pq For i If Bp [ pp ] Then

A[ i ] pp Else
A [ i ] pq Return(A)
End

На основании указанного количества операций можно получить трудоемкость процедуры слияния отсортированных массивов в среднем:

(m) = 2+2+1+3+2+1+kp*7+3+2+1+kq*7+3+1+2+1+m*(3+3+3+2) = 11*m + 7*(kp+kq) + 23 = 18*m+23. (10.1)

Подсчет вершин в дереве рекурсивных вызовов

Алгоритм, получая на входе массив из n элементов, делит его пополам при первом вызове, поэтому рассмотрим случай, когда n=, k =

В этом случае мы имеем полное дерево рекурсивных вызовов глубиной k, содержащее n листьев, фрагмент дерева показан на рис 10. 1.

Рис 10.1 Фрагмент рекурсивного дерева при сортировке слиянием

Обозначим количество вершин дерева через V:
V = n + n/2+n/4+n/8+…+1 = n*(1+1/2+1/4+1/8+…+1)=2n — 1= — 1

Из них все внутренние вершины порождают рекурсию, количество таких вершин – Vr = n-1, остальные n вершин – это вершины в которых рассматривается только один элемент массива, что приводит к останову рекурсии.

Анализ трудоемкости алгоритма сортировка слиянием

Таким образом, для n листьев дерева выполняется вызов процедуры MS c вычислением r+1, проверка условия p=q и возврат в вызывающую процедуру для слияния, что в сумме с учетом трудоемкости вызова даёт:
F1(n) = n*2*(5+4+1) + n*2(If p=q и r+1) = 22*n;

Для n-1 рекурсивных вершин выполняется проверка длины переданного массива, вычисление середины массива, рекурсивный вызов процедур MS, и возврат, поскольку трудоемкость вызова считается при входе в процедуру, то мы получаем:

Fr(n) = (n-1)*2*(5+4+1) + (n-1)*(1+3+1) = 24*n — 24;

Процедура слияния отсортированных массивов будет вызвана n-1 раз, при этом трудоемкость складывается из трудоемкости вызова и собственной трудоемкости процедуры Merge:
Трудоемкость вызова составит (для 6 параметров и 4-х регистров):
Fm(n) = (n-1)*2*(6+4+1) = 22*n — 22;

Поскольку трудоемкость процедуры слияния для массива длиной m составляет 18*m + 23 (10.

1), и процедура вызывается n-1 раз с длинами массива равными n, n/2, n/4, …, причем 2 раза с длиной n/2, 4 раза с длиной n/4, то со-вокупно имеем:
Fm(n) = (n-1)*23 + 18*n + 2*18*(n/2) + 4*18*(n/4) + … + =
= {учитывая, что таким образом обрабатывается k-1 уровней}
= 18*n *( – 1) + 23*(n-1) = 18*n* + 5*n — 23;

Учитывая все компоненты функции трудоемкости, получаем окончательную оценку:
Fa(n) = F1(n) + Fr(n) + Fm(n) + Fm(n) =
= 22*n + 24*n — 24 + 22*n — 22 +18*n* + 5*n — 23 =
= 18*n* + 73*n — 69 (10.2)

Если количество чисел на входе алгоритма не равно степени двойки, то необходимо проводить более глубокий анализ, основанный на изучении поведения рекурсивного дерева, однако при любых ситуациях с данными оценка главного порядка Q( n* ) не измениться.

Рекурсия: прямая против косвенной | Baeldung по компьютерным наукам

1. Введение

В этом руководстве мы рассмотрим концепции прямой и косвенной рекурсии , которые являются фундаментальными принципами программирования.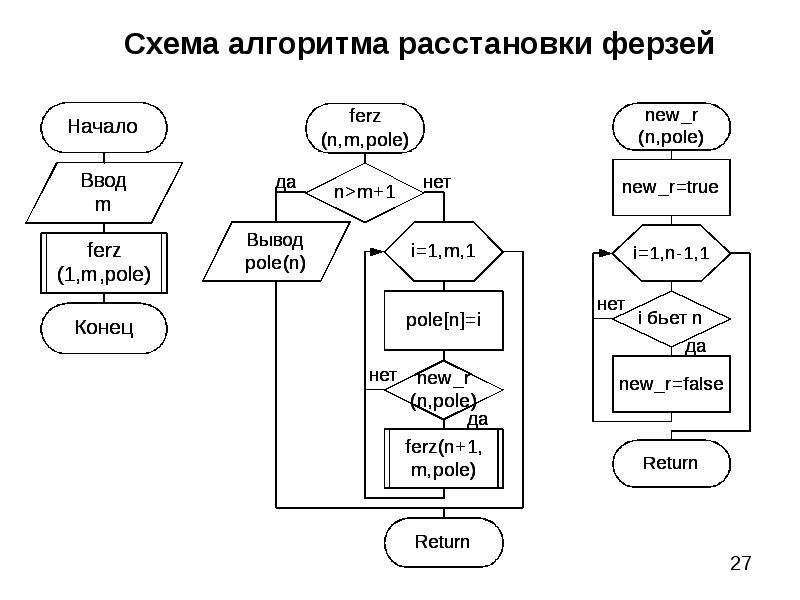 Мы также выделим их преимущества и недостатки. Понимание разницы между прямой и косвенной рекурсией необходимо для ее эффективного использования.

2. Рекурсия

Рекурсия — это подход к программированию, при котором функция вызывает сама себя, намереваясь решить проблему. Это мощный инструмент для решения широкого круга задач. Однако важно использовать его осторожно, чтобы избежать бесконечных циклов и других проблем.

Рекурсивная функция состоит из двух ключевых элементов: базового и рекурсивного случая. Базовый случай относится к условию остановки рекурсии. С другой стороны, рекурсивный случай определяет логику функции для решения проблемы, вызывая саму себя с модифицированной версией исходного ввода.

Вот пример простой рекурсивной функции, которая суммирует все элементы в списке:

В этом примере базовым случаем является условие if <= 0 , которое верно, когда входной список пуст.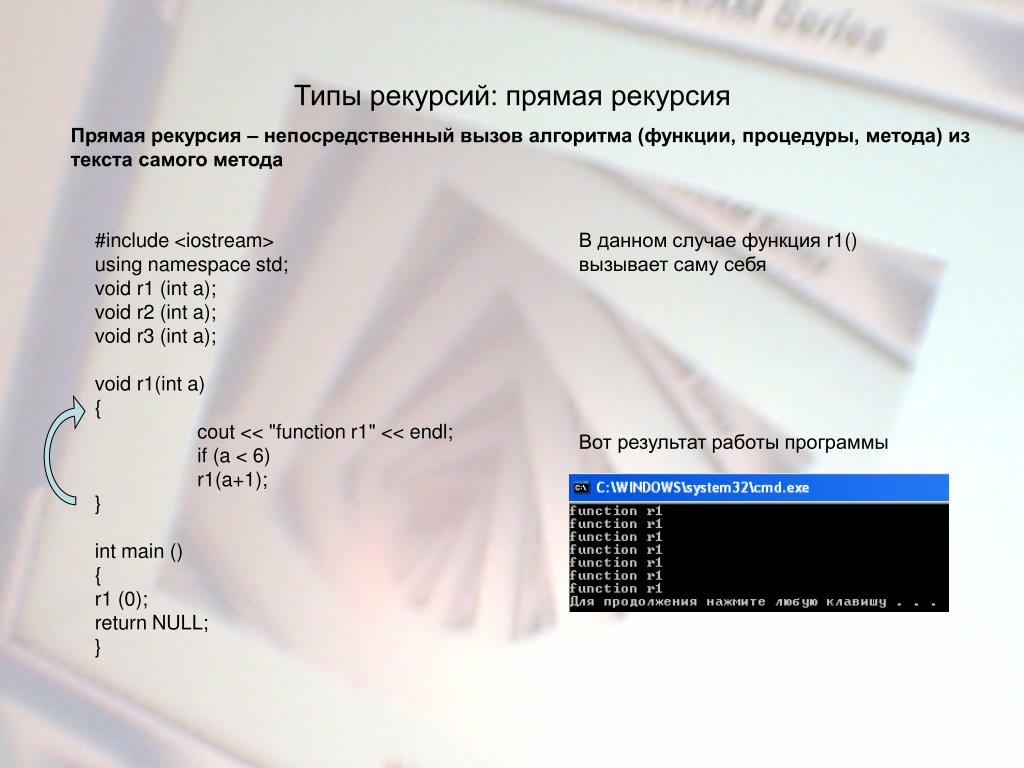 Рекурсивный случай — это оператор return return my_list[size-1] + sum_my_list(my_list, size-1) , который вызывает саму функцию с измененным списком, в котором отсутствует первый элемент. Рекурсия продолжается до тех пор, пока не будет достигнут базовый вариант, после чего функция возвращает окончательный результат.

важно понимать, как работает рекурсия и как ее использовать для достижения оптимальных результатов, чтобы избежать распространенных ошибок. В следующих разделах мы рассмотрим два типа рекурсии: прямую рекурсию и косвенную рекурсию.

3. Прямая рекурсия

Прямая рекурсия — это тип рекурсии, при котором функция напрямую вызывает сама себя в своем собственном блоке кода . Это означает, что функция появляется как часть определения функции, и функция вызывает себя для выполнения своей задачи.

Прямая рекурсивная функция для вычисления факториала заданного числа является примером прямой рекурсии. Факториал числа получается путем умножения всех положительных целых чисел, меньших или равных этому числу. Например, если мы возьмем число 6, факториал 6 (записывается как 6!) будет 6x5x4x3x2x1=720. Следующее определение представляет прямую рекурсивную функцию для определения факториала числа:

В этом примере функция вызывается со значением число-1 в качестве параметра. Рекурсия заканчивается, когда выполняется базовый случай number=1 . На этом этапе функция возвращает окончательный результат.

3.1. Преимущества и недостатки прямой рекурсии

Существует несколько преимуществ использования прямой рекурсии. Одним из преимуществ является то, что часто проще писать и понимать прямые рекурсивные функции , так как базовый и рекурсивный случаи четко определены в одной и той же функции.

Кроме того, в некоторых сценариях использование прямой рекурсии может привести к повышению эффективности, поскольку позволяет избежать накладных расходов на вызов дополнительной функции.

Однако у прямой рекурсии есть и недостатки:

Одним из недостатков является то, что отладка прямых рекурсивных функций может представлять большие трудности , так как стек вызовов может стать очень большим и, вероятно, станет трудно отслеживать выполнение функции. Кроме того, прямая рекурсия может потреблять большой объем памяти, если рекурсия не завершена должным образом, поскольку каждый рекурсивный вызов добавляет новый уровень в стек вызовов.

В целом, крайне важно вдумчиво оценить баланс между простотой, эффективностью и отладкой при принятии решения об использовании прямой рекурсии в данной ситуации.

4. Косвенная рекурсия

При косвенной рекурсии функция вызывает другую функцию, которая затем снова вызывает первую функцию . Рекурсия заканчивается, когда выполняется базовый случай, на этом этапе процесс останавливается.

Примером косвенно-рекурсивной функции является функция, которая решает, является ли заданное число четным или нечетным. Рассмотрим пример:

В этом примере функция isEven определяется с помощью функции isOdd , а функция isOdd определяется с помощью функции isEven . Это создает косвенную рекурсивную связь между двумя функциями.

Функция isEven является базовым вариантом для функции isOdd , а функция isOdd является базовым вариантом для функции isEven . Рекурсия продолжается до тех пор, пока не будет достигнут один из базовых случаев, после чего функция выдает истинный или ложный вывод, показывающий, является ли входное число четным или нечетным.

4.1. Преимущества и недостатки косвенной рекурсии

Одним из преимуществ косвенной рекурсии является то, что часто легче понять и отладить , так как базовый и рекурсивный случаи определяются в отдельных функциях.

Кроме того, непрямая рекурсия в некоторых случаях может привести к повышению эффективности, поскольку она допускает более модульную структуру и может уменьшить размер стека вызовов.

Однако у использования косвенной рекурсии есть и недостатки:

Одним из недостатков является сложность написания и понимания , так как логика разделена между двумя функциями. Кроме того, косвенная рекурсия в некоторых случаях может потреблять больше памяти, так как требует создания дополнительных вызовов функций. Крайне важно вдумчиво оценить баланс между сложностью, эффективностью и модульностью при принятии решения об использовании косвенной рекурсии в данной ситуации.

5. Различия между прямой и косвенной рекурсией

6. Заключение

В этой статье мы рассмотрели концепции прямой и косвенной рекурсии, а также преимущества и недостатки каждого типа рекурсии. Мы также сравнили сходства и различия между двумя типами рекурсии.

Мы узнали, что при прямой рекурсии функция вызывает сама себя непосредственно в своем собственном теле. Принимая во внимание, что косвенная рекурсия обычно включает как минимум две функции. Функция вызывает вторую функцию, которая затем снова вызывает первую функцию.

Алгоритмический дизайн: рекурсия — проект CodeIT

Рекурсия — это мощный инструмент, с помощью которого алгоритм может быть выражен в терминах самого себя. Он обеспечивает простой и мощный способ решения множества проблем. Часто бывает трудно думать о том, как решить проблему рекурсивно. Также очень легко написать рекурсивный алгоритм, который либо слишком долго выполняется, либо не завершается должным образом.

В этом подразделе мы рассмотрим основы рекурсии, чтобы предоставить читателю возможность понять, как можно легко решить сложные проблемы с помощью рекурсивного мышления.

Первое, что нужно сделать, это ответить на вопрос: «что такое рекурсия?»

Рисунок 7 – Рекурсия
Источник: Shutterstock.com

Матрешки предлагают полезную аналогию для понимания рекурсии . Предположим, у вас есть алгоритм открытия каждой куклы. Затем, чтобы добраться до последней куклы, которую больше нельзя открыть, чтобы получить уменьшенную версию, вы будете выполнять один и тот же алгоритм каждый раз, пока не останется кукол, которые нужно открыть.

В разработке алгоритмов алгоритм называется рекурсивным, если он называет себя . Очевидно, что при работе с алгоритмом, который вызывает сам себя, возникает проблема, связанная с тем, что алгоритм в конечном итоге завершится и выдаст правильный результат. Цикличность рекурсивных алгоритмов можно избежать, гарантируя, что каждый раз входные данные для последовательного выполнения уменьшаются на некоторое число, так что в какой-то момент оно в конечном итоге станет равным нулю, и алгоритм завершится.

Для реализации рекурсивного алгоритма задача должна удовлетворять следующим условиям:

• Ее можно разбить на более простую версию той же задачи
• Она имеет один или несколько базовых случаев, значения которых известны

Вот реальный пример рекурсии: представьте, что вы сидите в последнем ряду кинотеатра и хотите подсчитать количество рядов. Вы просите человека, сидящего перед вами, сказать вам, сколько рядов перед ним. Этот человек делает то же самое и спрашивает человека, сидящего перед ним, и так далее, пока вопрос не будет задан человеку, сидящему в первом ряду. Этот человек может ответить ноль человеку позади него, потому что он видит, что перед ним больше нет рядов. Это базовый случай. Человек во втором ряду добавляет 1 к ответу и сообщает его человеку позади него в третьем ряду и так далее, пока ответ не дойдет до вас. Обратите внимание, что на каждом этапе задача сводится к более простой версии той же задачи.

Давайте теперь рассмотрим пример с использованием алгоритма. Во-первых, рассмотрим модуль (в языках программирования это называется процедурой, функцией, процессом или подпрограммой), который печатает фразу «Привет, энтузиасты CodeIT» всего X раз:

модуль Hello(X)
if(X<1 )
return print(«Привет, энтузиасты CodeIT!»)
Hello(X – 1)

Давайте смоделируем выполнение, вызвав модуль Hello со значением для X = 10.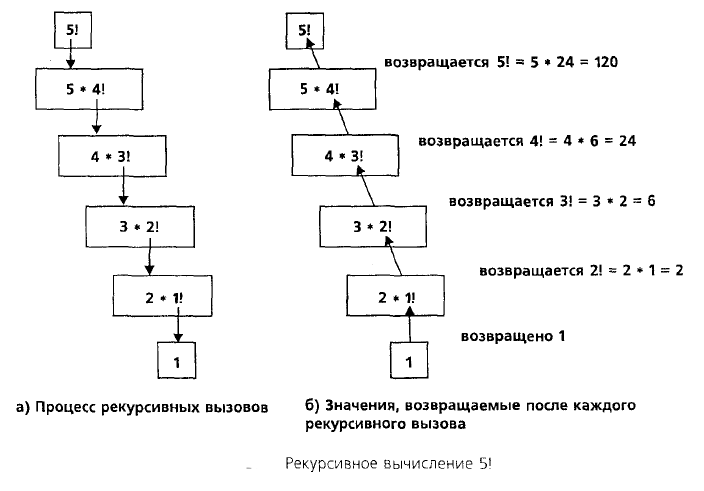 Поскольку X не меньше 1, мы ничего не делаем на первая строка. Далее мы печатаем «Привет, энтузиасты CodeIT!» один раз. На данный момент нам нужно напечатать нашу фразу 9больше раз. Поскольку теперь у нас есть модуль Hello, который может сделать именно это, мы просто вызываем Hello (на этот раз с X, установленным на 9), чтобы напечатать оставшиеся копии. Этот экземпляр Hello напечатает фразу один раз, а затем вызовет другую копию Hello, чтобы напечатать оставшиеся 8. Это будет продолжаться до тех пор, пока, наконец, мы не вызовем Hello с X, равным нулю. Hello(0) ничего не делает; он просто возвращается. Как только Hello(0) завершается, Hello(1) также завершается и возвращается. Это продолжается вплоть до нашего первоначального вызова Hello(10), который завершает выполнение, выводя в общей сложности 10 «Привет, энтузиасты CodeIT!».

Вот некоторые ключевые соображения при разработке рекурсивного алгоритма:

• Он обрабатывает простую общую ситуацию без использования рекурсии: В приведенном выше примере общей ситуацией является Hello(0). Если модулю предлагается напечатать ноль раз, он возвращается, не порождая больше «Привет, энтузиасты CodeIT».
• Позволяет избежать циклов. Представьте, что Hello(10) вызывает Hello(10), который вызывает Hello(10). В итоге вы получите бесконечный цикл вызовов, и это обычно приводит к ошибке «переполнения стека» при работе на компьютере. Во многих рекурсивных программах можно избежать циклов, вызывая каждый модуль для решения задачи, которая каким-то образом меньше или проще исходной задачи. В этом случае, например, X будет с каждым вызовом все меньше и меньше. По мере того, как задача становится все проще и проще (в этом случае мы будем считать «простым» напечатать что-то ноль раз, а не 5 раз), в конечном итоге она придет к общей ситуации и остановит рекурсию. Есть много способов избежать бесконечных циклов, но хорошее эмпирическое правило заключается в том, чтобы убедиться, что мы имеем дело с постепенно меньшими или более простыми проблемами.
• Каждый вызов модуля представляет собой полную обработку данной задачи. Иногда кажется, что рекурсия волшебным образом решает большие проблемы, но на самом деле это не так. Когда нашему модулю передается аргумент 10, мы печатаем «Привет, энтузиасты CodeIT!» один раз, а затем мы печатаем его еще 9 раз. Мы можем передать часть задания рекурсивному вызову, но исходная функция все равно должна каким-то образом учитывать все 10 копий.

Одна из причин, по которой рекурсия немного сбивает с толку, заключается в том, что она не следует прямому естественному образу мышления, как в случае с итерацией.

Рекурсивный алгоритм подразумевает, что рекурсивная модульная часть алгоритма должна сначала вызываться извне модуля, но затем она продолжает вызывать себя внутри модуля, пока не достигнет условия завершения. С точки зрения компьютера, если модуль вызывает сам себя или вызывает другой модуль, это все еще обычный вызов модуля, если предоставлены необходимые входные параметры.

Рекурсия следует методу разработки алгоритма «разделяй и властвуй», который означает разбиение проблемы на подзадачи того же или родственного типа, пока подзадача не станет достаточно простой, чтобы ее можно было решить напрямую. Затем решения подзадач объединяются, чтобы дать решение исходной проблемы. Итак, как разделяй и властвуй относится к модулю, вызывающему сам себя? При первом вызове рекурсивного модуля предоставляется полное входное значение, в тот момент, когда модуль начинает вызывать сам себя, каждый раз, когда в каждой единице вызова, входные данные достаточно просты, чтобы обеспечить решение в одном вызов.

Оказывается, для любого алгоритма, использующего рекурсию, может быть эквивалентный алгоритм, использующий итерацию. Таким образом, рекурсию также можно рассматривать как другую форму итерации. Тем не менее, рекурсивный алгоритм описания конкретного процесса часто гораздо более лаконичен, чем итерационный.

Возможно, самым известным примером проблемы, которую можно решить с помощью рекурсии более эффективно, чем понять и решить с помощью итерации, являются Ханойские башни.

Наконец, как известно, рекурсия очень важна в разработке игр. Вот несколько примеров частого использования в разработке игр (Quora.