Связанные списки в Python
Связанный список — это линейная структура данных, элементы которой не хранятся в непрерывном месте. Это означает, что связанный список содержит отдельные вакуоли, известные как «узлы», которые содержат данные, для которых они были созданы, и ссылку на другой узел в списке.
Некоторыми преимуществами связного списка являются его прерывистый характер и время чтения, никогда не превышающее O(n). Связанный список не нужно хранить постоянно, потому что он имеет ссылки, встроенные в каждый узел, для расположения следующего по порядку. Если в памяти вашего компьютера мало места, идеально подойдет связанный список, поскольку всю структуру не нужно хранить в одном месте. Это также означает, что чтение связанного списка является линейным, поскольку размер списка приближается к бесконечности.
Однако недостатки делают его особенным. Кроме того, если в список вносится добавление, необходимо обновить весь список, чтобы ссылки оставались правильными.
В этой статье мы рассмотрим концепцию единственных и двусвязных списков и некоторые общие вопросы интервью, которые могут появиться для каждого из них.
Односвязный список состоит из нескольких узлов, каждый из которых содержит а) данные и б) ссылку на следующий узел.
На изображении выше мы видим макет связанного списка. Начиная слева и продвигаясь вправо, мы видим, что заголовок списка содержит данные и указатель на следующий узел. Этот шаблон продолжается до конца списка, где он не является узлом. Значение NULL означает, что список закончился.
Посмотрите ниже код для создания односвязного списка.
# Node class
class Node:
# Function to initialize the node object
def __init__(self, data):
self.data = data # Assign data
self. nextnode = None # Initialize next as null
a = Node(1) # declaring data in each node
b = Node(2)
c = Node(3)
a.nextnode = b # link first node to second node
b.nextnode = c # link second node to third node
a.next.value # will return the value of the next node b = 2
nextnode = None # Initialize next as null
a = Node(1) # declaring data in each node
b = Node(2)
c = Node(3)
a.nextnode = b # link first node to second node
b.nextnode = c # link second node to third node
a.next.value # will return the value of the next node b = 2
В двусвязном списке каждый узел содержит данные, ссылку на узел, после него, и ссылку на узел, предшествующий ему.
Разница между односвязным списком и двусвязным списком — это «предыдущие» стрелки, указанные на рисунке выше. Преимущества дополнительного указателя означают, что список можно перемещать в любом направлении при доступе к информации — это означает, что переход от узла 5 к узлу 8 может быть проще, чем обход с начала списка.
Новые узлы в начале и в конце списка называются «дозорными». Эти узлы заменяют значения NULL, которые вы видите выше. Они позволяют быстро вставлять или удалять вверху или внизу списка.
Посмотрите ниже код для двусвязного списка.
# Code to create the nodes for a doubly linked list
# A linked list node
class Node:
def __init__(self):
self. data = None # container of the data
self.next_node = None # standard pointer to next node
self.prev_node = None # pointer to previous node
# Creating each node
a = Node(1)
b = Node(2)
c = Node(3)
# Connect the nodes
# Connect nodes a & b to each other in both directions
a.next_node = b
b.prev_node = a
# Connect nodes b & c to each other in both directions
b.next_node = c
c.prev_node = b
"""
We could create a circularly linked list by connecting the head of the list
to the tail
"""
data = None # container of the data
self.next_node = None # standard pointer to next node
self.prev_node = None # pointer to previous node
# Creating each node
a = Node(1)
b = Node(2)
c = Node(3)
# Connect the nodes
# Connect nodes a & b to each other in both directions
a.next_node = b
b.prev_node = a
# Connect nodes b & c to each other in both directions
b.next_node = c
c.prev_node = b
"""
We could create a circularly linked list by connecting the head of the list
to the tail
"""
Теперь, когда у нас есть код, необходимый для создания связанных списков, давайте рассмотрим некоторые общие вопросы собеседования, варианты которых вы можете найти на Leetcode.
1. Сторнирование связанного списка
Создайте функцию, чтобы перевернуть связанный список на месте. Вы будете использовать заголовок исходного списка и возвращать заголовок перевернутого списка.
Уловка, стоящая за этой проблемой, заключается в том, что разворот должен происходить в постоянном пространстве. Поэтому мы не создаем новый список и не добавляем или не используем прокси. Это необходимо сделать, работая непосредственно с этим списком.
Поэтому мы не создаем новый список и не добавляем или не используем прокси. Это необходимо сделать, работая непосредственно с этим списком.
def reversal(head):
# set variables for the node position
current = head #
prev = None
next_node = None
# let's us know that we haven't reached the end of the list
while current:
# copy the pointer of the head before we override it
next_node = current.nextnode
# change the pointer to point at None (because it is the new tail)
current.nextnode = prev
# move us along on the list, current becomes previous
prev = current
# and the next node becomes the current node we are looking at
current = nextnode
return prev
Как объяснено в приведенном выше коде, мы, по сути, просто переключаем указатели для каждого узла. Входными данными является текущая глава связанного списка — или в наших примерах. Затем функция проходит через каждый узел и переключает направление атрибута nextnode.
Этот подход имеет то преимущество, что снижает затраты на память и впечатляет интервьюеров своей способностью работать без создания нового списка и удержания процесса на O(n) времени.
2. Связанный список с N-го до последнего узла
Создайте функцию, которая принимает головной узел и целое число n, а затем возвращает n-й и последний узел из списка.
Уловка для этой задачи состоит в том, чтобы пройти по списку двумя маркерами. Первый маркер выполняет итерацию и проверяет, действительно ли существует предпоследний узел. Второй маркер идет позади и заканчивается в этом узле.
def nth_last_node(n,head):
# create two pointers that both start at the head of the list
pointer_1 = head
pointer_2 = head
# we will iterate through the list, moving the right pointer
# until there are n-spaces between them
for i in range(n-1):
# edge case, if no nextnode, raise an error
if not pointer_1. nextnode:
raise LookupError('Error: Command continues past index of list')
# if not edge case, move the right pointer to next node
pointer_1 = pointer_1.nextnode
# now there is a n-size block between them
# as long as the right pointer does not reach the end of the list
# the left pointer will move
while pointer_1.nextnode:
# once the right pointer hits the end the left pointer has found the
# nth to last node from the end
pointer_2 = pointer_2.nextnode
pointer_1 = pointer_1.nextnode
# return the nth to last node
return pointer_2
nextnode:
raise LookupError('Error: Command continues past index of list')
# if not edge case, move the right pointer to next node
pointer_1 = pointer_1.nextnode
# now there is a n-size block between them
# as long as the right pointer does not reach the end of the list
# the left pointer will move
while pointer_1.nextnode:
# once the right pointer hits the end the left pointer has found the
# nth to last node from the end
pointer_2 = pointer_2.nextnode
pointer_1 = pointer_1.nextnode
# return the nth to last node
return pointer_2
Хотя код отлично справляется с созданием пространства между ними, давайте посмотрим на визуальный элемент.

Вот и все. У нас были базовые основы того, что такое связанный список, и какие вопросы по нему можно задать.
16. Связные списки — Учимся с Python
16.1. Знакомьтесь: связный список
Мы уже видели примеры атрибутов, которые ссылаются на другие объекты. Ссылки на объекты использует и широко известная структура данных связный список
Связные списки состоят из узлов, каждый из которых содержит ссылку на следующий узел в списке. Кроме того, каждый узел содержит какие-то полезные данные.
Связный список относится к рекурсивным структурам данных, поскольку его определение рекурсивно.
Связный список представляет собой либо
- пустой список, представленный значением None, либо
- узел, содержащий данные и ссылку на связный список.
Рекурсивные структуры данных могут обрабатываться рекурсивными методами.
16.2. Класс Node
Как обычно при определении нового класса, мы начнем с инициализирующего метода и метода __str__, обеспечив возможность создания и отображения объектов нового класса:
class Node:
def __init__(self, cargo=None, next=None):
self. cargo = cargo
self.next = next
def __str__(self):
return str(self.cargo)
cargo = cargo
self.next = next
def __str__(self):
return str(self.cargo)
Параметры инициализирующего метода опциональны. По умолчанию и данные, cargo, и ссылка, next, получают значения None.
Строковым представлением узла будет строковое представление данных этого узла. Поскольку функции str можно передать любое значение, в нашем узле можно хранить любое значение.
Для тестирования создадим объект Node и выведем его на печать:
>>> node = Node("test")
>>> print node
test
Чтобы было интереснее, нам нужен список с более чем одним узлом:
>>> node1 = Node(1) >>> node2 = Node(2) >>> node3 = Node(3)
Этот код создает три узла, но у нас нет списка, так как ни один узел не связан с другим. Посмотрите на рисунок:
Чтобы связать узлы, нам нужно заставить первый узел ссылаться на второй, а второй — на третий:
>>> node1.next = node2 >>> node2.next = node3
Ссылка в третьем узле имеет значение None, что означает конец списка.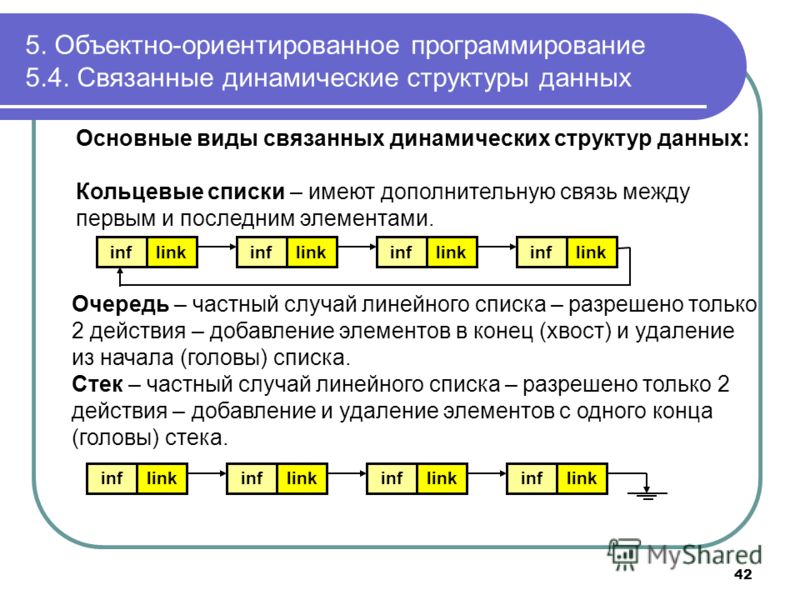
Теперь вы знаете, как создавать узлы и связывать их в списки. Но, возможно, пока не понимаете, зачем это нужно.
16.3. Списки как коллекции
Списки полезны, поскольку дают возможность собрать многочисленные объекты в единую сущность, иногда называемую коллекцией. В примере выше, первый узел списка может служить ссылкой на весь список.
Чтобы передать связный список в качестве аргумента, достаточно передать ссылку на первый узел. Например, функция print_list принимает один узел в качестве аргумента. Начиная с первого узла списка, она выводит на печать каждый узел, пока не достигнет конца списка:
def print_list(node):
while node:
print node,
node = node.next
print
Вызовем функцию, передав ей ссылку на первый узел:
>>> print_list(node1) 1 2 3
Хотя у print_list есть ссылка на первый узел списка, внутри функции нет переменных, ссылающихся на другие узлы. Функция получает ссылку на следующий узел, используя значение атрибута next каждого узла.
Чтобы пройти весь связный список, обычно используют переменную цикла вроде node, которая последовательно получает значения, ссылающиеся на узлы списка.
16.4. Списки и рекурсия
Многие операции над списком естественно реализовать с помощью рекурсивных методов. Вот рекурсивный алгоритм для вывода на печать списка в обратном порядке:
- Разделить список на две части: первый узел (голова) и все остальные (хвост).
- Распечатать хвост в обратном порядке.
- Распечатать голову.
Разумеется, шаг 2, рекурсивный вызов, предполагает, что у нас имеется способ распечатать список в обратном порядке. Но если мы примем, что рекурсивный вызов работает – нужно в это поверить – то мы можем убедиться в том, что алгоритм работает.
Все, что нам нужно, это простейший случай списка (базовый случай) и доказательство того, что, какой бы список мы ни взяли, наш алгоритм в конце концов приведет нас к этому базовому случаю. Имея рекурсивное определение списка, приведенное выше, в качестве базового случая возьмем пустой список, представленный значением None:
def print_backward(list):
if list == None: return
head = list
tail = list. next
print_backward(tail)
print head,
next
print_backward(tail)
print head,
Первая строка обрабатывает базовый случай. Две следующие строки кода разделяют список на head (англ.: голова) и tail (англ.: хвост). Две последние строки кода выводят список на печать. Запятая в конце последней строки удерживает Python от перевода строки после печати каждого узла.
Вызовем функцию так же, как вызывали print_list:
>>> print_backward(node1) 3 2 1
В результате на печать выведен список в обратном порядке.
Возможно, вы недоумеваете, почему print_list и print_backward являются функциями, а не методами класса Node. Причина в том, что мы используем None для представления пустого списка, а вызвать метод для None нельзя. Это ограничение не позволяет написать чистый объектно-ориентированный код для манипулирования списком.
Но можем ли мы доказать, что print_backward всегда завершится? Другими словами, всегда ли алгоритм приведет нас к базовому случаю? На самом деле, ответ отрицательный.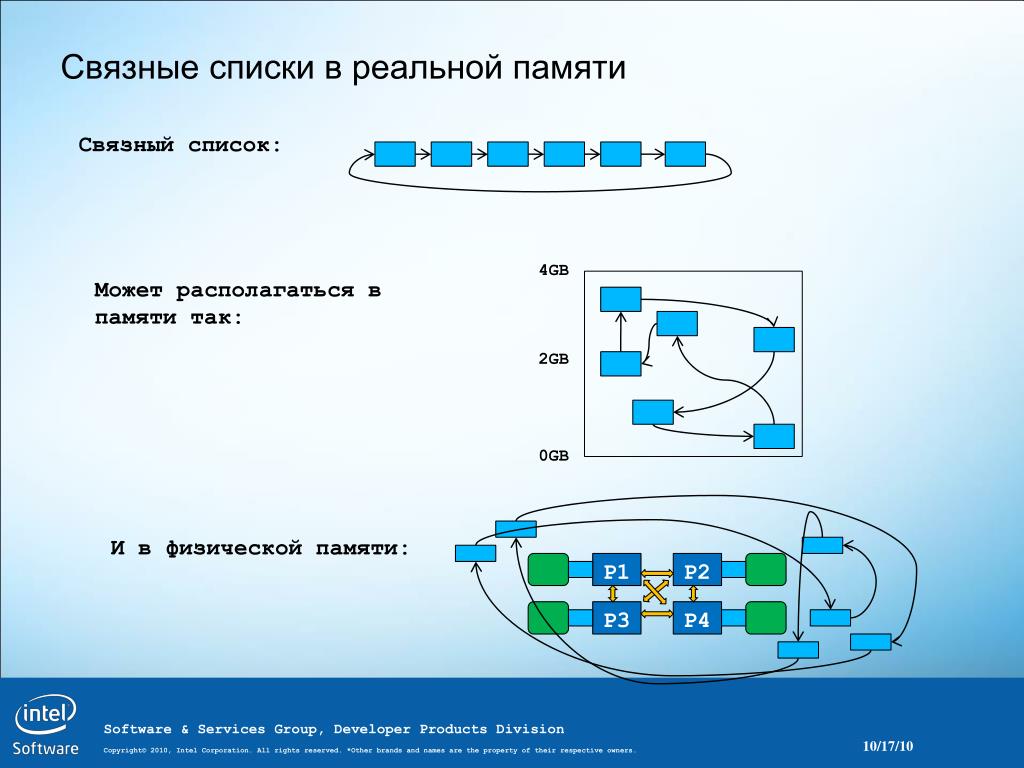 Некоторые списки сломают наш метод.
Некоторые списки сломают наш метод.
16.5. Бесконечные списки
Нет ничего, что помешало бы некоторому узлу ссылаться на узел, который идет в списке раньше этого узла, или ссылаться на самого себя. Например, этот рисунок показывает список с двумя узлами, один из которых ссылается на себя!
Если вызвать print_list с этим списком, функция зациклится. Если вызвать print_backward, возникнет бесконечная рекурсия. Таким образом, работа с бесконечными списками сопряжена с определенными сложностями.
Тем не менее, иногда бесконечные списки полезны. Например, можно представить число как список цифр, и воспользоваться бесконечным списком для представления дробного периода этого числа.
И все же тот факт, что мы не можем доказать, что print_list и print_backward завершатся, представляет проблему. Лучшее, что мы можем сделать, это выдвинуть гипотезу: Если список не содержит циклов, то эти методы завершатся. Такого рода утверждения называются предусловием. Предусловие налагает ограничение на параметры и описывает поведение функции в случае, когда это ограничение выполняется. Вскоре мы встретимся с другими примерами предусловий.
Предусловие налагает ограничение на параметры и описывает поведение функции в случае, когда это ограничение выполняется. Вскоре мы встретимся с другими примерами предусловий.
16.6. Неоднозначность ссылки на узел списка
Следующий фрагмент print_backward может вызвать удивление:
head = list tail = list.next
После выполнения первого предложения присваивания head и list имеют один и тот же тип и одно и то же значение. В таком случае, зачем мы создаем новую переменную?
Причина в том, что эти две переменные играют разные роли. Мы думаем о head как о ссылке на один узел, а о list – как о ссылке на первый узел списка. Эти роли не являются частью программы; они существуют в уме программиста.
В общем случае, глядя на код программы, мы не можем сказать, какую роль играет та или иная переменная. Эта неоднозначность может быть полезной, но также может затруднить чтение программы. Часто, чтобы подчеркнуть роль, которую играет переменная, мы используем переменные с “говорящими” именами, например, node и list, а иногда создаем дополнительные переменные с этой целью.
Можно переписать print_backward без переменных head и tail, что сделает функцию более компактной, но менее ясной:
def print_backward(list) :
if list == None : return
print_backward(list.next)
print list,
Глядя на два вызова функции, нужно помнить, что print_backward рассматривает свой аргумент как коллекцию, а print – как единичный объект.
Если же взять ссылку на узел связного списка вне контекста, то ее семантика неоднозначна. Ссылка на узел связного списка может рассматриваться как ссылка на один узел или как ссылка на список.
16.7. Изменение списков
Можно изменить список двумя способами. Очевидно, что мы можем изменить данные одного из узлов. Но более интересны операции по добавлению, удалению и перестановке узлов.
В качестве примера давайте напишем функцию, которая удаляет второй узел из списка и возвращает ссылку на удаленный узел:
def remove_second(list):
if list == None: return
first = list
second = list. next
# make the first node refer to the third
first.next = second.next
# separate the second node from the rest of the list
second.next = None
return second
next
# make the first node refer to the third
first.next = second.next
# separate the second node from the rest of the list
second.next = None
return second
Здесь мы вновь используем временные переменные для того, чтобы сделать код яснее. Воспользуемся этой функцией:
>>> print_list(node1) 1 2 3 >>> removed = remove_second(node1) >>> print_list(removed) 2 >>> print_list(node1) 1 3
Следующий рисунок иллюстрирует результат работы функции remove_second:
А что случится, если вызвать эту функцию со списком из одного элемента? С пустым списком? Существует ли предусловие для этой функции? Если да, то добавьте в функцию проверку предусловия и обработку его нарушения.
16.8. Обертки и помощники
Если нам понадобится вывести связный список в обратном порядке, заключенный в квадратные скобки, то, как вариант, мы можем воспользоваться функцией print_backward чтобы вывести 3 2 1, и отдельно вывести открывающую и закрывающую скобки. Назовем новую функцию print_backward_nicely:
Назовем новую функцию print_backward_nicely:
def print_backward_nicely(list) :
print "[",
print_backward(list)
print "]",
В любом месте программы можно вызвать функцию print_backward_nicely, а она, в свою очередь, вызовет print_backward. Здесь print_backward_nicely работает как обертка, используя функцию print_backward в качестве помощника.
16.9. Класс LinkedList
У нашей реализации связных списков есть одна проблема, неочевидная на первый взгляд. Поменяв местами причину и следствие, предложим вначале альтернативную реализацию, а затем рассмотрим, какую проблему она решает.
Создадим новый класс LinkedList. Его атрибутами будут целое число, представляющее длину списка, и ссылка на первый узел списка. С помощью объектов LinkedList удобно манипулировать списками объектов Node:
class LinkedList:
def __init__(self):
self.length = 0
self.head = None
Класс LinkedList оказывается удобным местом для помещения в него таких функций, как print_backward_nicely, и превращения их в методы этого класса:
class LinkedList:
. ..
def print_backward(self):
print "[",
if self.head != None:
self.head.print_backward()
print "]",
class Node:
...
def print_backward(self):
if self.next != None:
tail = self.next
tail.print_backward()
print self.cargo,
..
def print_backward(self):
print "[",
if self.head != None:
self.head.print_backward()
print "]",
class Node:
...
def print_backward(self):
if self.next != None:
tail = self.next
tail.print_backward()
print self.cargo,
Мы переименовали print_backward_nicely, и теперь у нас два метода с именами print_backward: один в классе Node (помощник), и один в классе LinkedList (обертка). Когда метод-обертка вызывает self.head.print_backward, он вызывает метод-помощник, поскольку self.head ссылается на объект Node.
Еще один плюс класса LinkedList состоит в том, что он облегчает добавление и удаление первого элемента списка. Например, следующий метод add_first класса LinkedList принимает в качестве аргумента данные для узла и помещает новый узел с этими данными в начало списка:
class LinkedList:
...
def add_first(self, cargo):
node = Node(cargo)
node.next = self.head
self. head = node
self.length += 1
head = node
self.length += 1
Создадим связный список, добавим в него три узла и выведем его на печать в обратном порядке:
>>> linkedlist = LinkedList() >>> linkedlist.add_first(1) >>> linkedlist.add_first(2) >>> linkedlist.add_first(3) >>> linkedlist.print_backward() [ 1 2 3 ]
Поскольку каждый раз новый узел добавляется в начало списка, то последовательно добавленные нами узлы со значениями 1, 2, 3 расположились в обратном порядке, и метод print_backward вывел узлы в порядке их добавления.
В качестве упражнений вам будет предложено добавить другие полезные методы в класс LinkedList и поэкспериментировать с ними.
16.10. Инварианты
Некоторые списки построены правильно; другие нет. Например, если список содержит цикл, он сломает многие из наших методов. Поэтому мы можем потребовать, чтобы списки не содержали циклов. Другое разумное требование состоит в том, чтобы значение length в объекте LinkedList всегда равнялось реальному числу узлов в списке.
Требования, подобные этим, называются инвариантами, поскольку, в идеале, они должны выполняться для каждого объекта в любой момент времени. Указание инвариантов для объектов — полезный прием программирования. Он облегчает доказательство корректности кода, проверку целостности структур данных, и способствует обнаружению ошибок.
Заметим, что в отдельные моменты времени инварианты все же не выполняются. Например, в середине метода addFirst, после того, как мы добавили узел, но перед тем, как мы увеличили length, инвариант оказывается нарушенным. Такого рода нарушение приемлемо; действительно, часто невозможно изменить объект, не нарушая инвариант хотя бы ненадолго. Достаточно потребовать, чтобы метод, который нарушает инвариант, восстанавливал его.
Если имеется значительный участок кода, в котором инвариант нарушен, важно отразить это в комментариях. Чтобы операции, зависящие от инварианта, не выполнялись, пока инвариант не восстановлен.
16.11. Глоссарий
- инвариант
- Утверждение, которое должно выполняться для объекта в любое время (за
исключением того времени, когда объект изменяется).

- обертка
- Метод, который выступает посредником между вызывающим кодом и методом-помощником; способствует упрощению и повышению надежности кода.
- помощник
- Метод, не вызываемый непосредственно, а используемый вызываемым методом для выполнения части работы.
- предусловие
- Утверждение, которое должно быть справедливым, для того чтобы функция выполнялась корректно.
- связный список
- Структура данных, реализующая коллекцию, используя последовательность связанных узлов.
- узел списка
- Элемент списка, обычно реализуемый как объект, содержащий ссылку на объект того же типа и некоторые полезные данные.
16.12. Упражнения
- Традиционно списки выводятся на печать в скобках, с запятыми между элементами, например: [1, 2, 3]. Добавьте в класс LinkedList метод print_list так, чтобы он возвращал список в таком формате.
- Добавьте в класс LinkedList метод last, который вернет последний узел в списке или None
в случае, когда список пуст.
 Протестируйте работу метода для пустого и непустого списков.
Протестируйте работу метода для пустого и непустого списков. - Добавьте в класс LinkedList метод append(self, cargo) для добавления узла в конец списка. Используйте метод list из предыдущего упражнения для получения узла, к которому будет добавляться новый узел. Протестируйте работу метода.
- Добавьте в класс LinkedList метод find(self, cargo) для поиска в списке узла с cargo, ближайшего к началу списка. Протестируйте метод для пустого списка, списка, содержащего узел с искомым cargo, и для списка, не содержащего такого узла.
- Добавьте в класс LinkedList метод __contains__(self, cargo) чтобы реализовать оператор in для LinkedList. Используйте метод find из предыдущего упражнения в методе __contains__. Протестируйте работу оператора in для пустого списка, списка, содержащего узел с cargo, и списка, не содержащего такого узла.
Связанные списки Python — pythobyte.com
Автор оригинала: Frank Hofmann.
Связанный список-одна из наиболее распространенных структур данных, используемых в информатике. Он также является одним из самых простых и фундаментален для структур более высокого уровня, таких как стеки, циклические буферы и очереди.
Он также является одним из самых простых и фундаментален для структур более высокого уровня, таких как стеки, циклические буферы и очереди.
Вообще говоря, список-это набор отдельных элементов данных, связанных ссылками. Программисты на языке Си знают это как указатели. Например, элемент данных может состоять из адресных данных, географических данных, геометрических данных, маршрутной информации или сведений о транзакциях. Обычно каждый элемент связанного списка имеет один и тот же тип данных, специфичный для данного списка.
Один элемент списка называется узлом. Узлы не похожи на массивы, которые последовательно хранятся в памяти. Вместо этого он, скорее всего, найдет их в разных сегментах памяти, которые вы можете найти, следуя указателям от одного узла к другому. Обычно конец списка помечается нулевым элементом, представленным эквивалентом Python None .
Рисунок 1: Односвязный список
Существует два вида списков – одинарные и двусвязные списки . Узел в односвязном списке указывает только на следующий элемент в списке, тогда как узел в двусвязном списке также указывает на предыдущий узел. Структура данных занимает больше места, потому что вам понадобится дополнительная переменная для хранения дальнейшей ссылки.
Структура данных занимает больше места, потому что вам понадобится дополнительная переменная для хранения дальнейшей ссылки.
Рисунок 2: Двусвязный список
Односвязный список можно пройти от головы до хвоста, в то время как обратный путь не так прост. Напротив, двусвязный список позволяет обходить узлы в обоих направлениях с одинаковой стоимостью, независимо от того, с какого узла вы начинаете. Кроме того, добавление и удаление узлов, а также разбиение односвязных списков выполняется не более чем в два этапа. В двусвязном списке необходимо изменить четыре указателя.
Язык Python не содержит предопределенного типа данных для связанных списков. Чтобы справиться с этой ситуацией, мы должны либо создать свой собственный тип данных, либо использовать дополнительные модули Python, которые обеспечивают реализацию такого типа данных.
В этой статье мы рассмотрим шаги по созданию собственной структуры данных связанного списка. Сначала мы создаем соответствующую структуру данных для узла. Во-вторых, вы узнаете, как реализовать и использовать как односвязный список, так и, наконец, двусвязный список.
Во-вторых, вы узнаете, как реализовать и использовать как односвязный список, так и, наконец, двусвязный список.
Шаг 1: Узел как структура данных
Чтобы иметь структуру данных, с которой мы можем работать, мы определяем узел. Узел реализуется как класс с именем ListNode . Класс содержит определение для создания экземпляра объекта, в данном случае с двумя переменными – data для сохранения значения узла и next для хранения ссылки на следующий узел в списке. Кроме того, узел имеет следующие методы и свойства:
__init_(): инициализировать узел с даннымиself.data: значение, хранящееся в узлеself.next: опорный указатель на следующий узелhas_value(): сравнение значения со значением узла
Эти методы гарантируют, что мы можем правильно инициализировать узел с нашими данными ( __init__ () ) и покрывать как извлечение данных, так и их хранение (через свойство self. ), а также получение ссылки на подключенный узел (через свойство  data
dataself.next ). Метод has_value() позволяет сравнить значение узла со значением другого узла.
Листинг 1: Класс ListNode
class ListNode:
def __init__(self, data):
"constructor to initiate this object"
# store data
self.data = data
# store reference (next item)
self.next = None
return
def has_value(self, value):
"method to compare the value with the node data"
if self.data == value:
return True
else:
return False
Создание узла так же просто, как и создание экземпляра объекта класса ListNode :
Листинг 2: Создание экземпляров узлов
node1 = ListNode(15) node2 = ListNode(8.2) node3 = ListNode("Berlin")
Сделав это, мы имеем в наличии три экземпляра класса ListNode . Эти экземпляры представляют собой три независимых узла, которые содержат значения 15 (целое число), 8.2 (поплавок) и “Берлин” (строка).
Шаг 2: Создание класса для односвязного списка
В качестве второго шага мы определяем класс с именем Single Linked List , который охватывает методы, необходимые для управления узлами списка. Он содержит эти методы:
__init__(): инициировать объектlist_length(): возвращает количество узловoutput_list(): выводит значения узловadd_list_item(): добавить узел в конец спискаunordered_search(): поиск в списке узлов с заданным значениемremove_list_item_by_id(): удалить узел в соответствии с его идентификатором
Мы рассмотрим каждый из этих методов шаг за шагом.
Метод __init__() определяет две внутренние переменные класса с именами head и tail . Они представляют собой начальный и конечный узлы списка. Изначально и
Они представляют собой начальный и конечный узлы списка. Изначально и head , и tail имеют значение None до тех пор, пока список пуст.
Листинг 3: Класс Single Linked List (часть первая)
class SingleLinkedList:
def __init__(self):
"constructor to initiate this object"
self.head = None
self.tail = None
return
Шаг 3: Добавление узлов
Добавление элементов в список осуществляется через add_list_item() . Этот метод требует узла в качестве дополнительного параметра. Чтобы убедиться, что это правильный узел (экземпляр класса ListNode ), параметр сначала проверяется с помощью встроенной функции Python isinstance() . В случае успеха узел будет добавлен в конец списка. Если
В случае успеха узел будет добавлен в конец списка. Если item не является ListNode , то он создается.
В случае, если список (все еще) пуст, новый узел становится главой списка. Если узел уже находится в списке, то значение tail корректируется соответствующим образом.
Листинг 4: Класс Single Linked List (часть вторая)
def add_list_item(self, item):
"add an item at the end of the list"
if not isinstance(item, ListNode):
item = ListNode(item)
if self.head is None:
self.head = item
else:
self.tail.next = item
self.tail = item
return
Метод list_length() подсчитывает узлы и возвращает длину списка.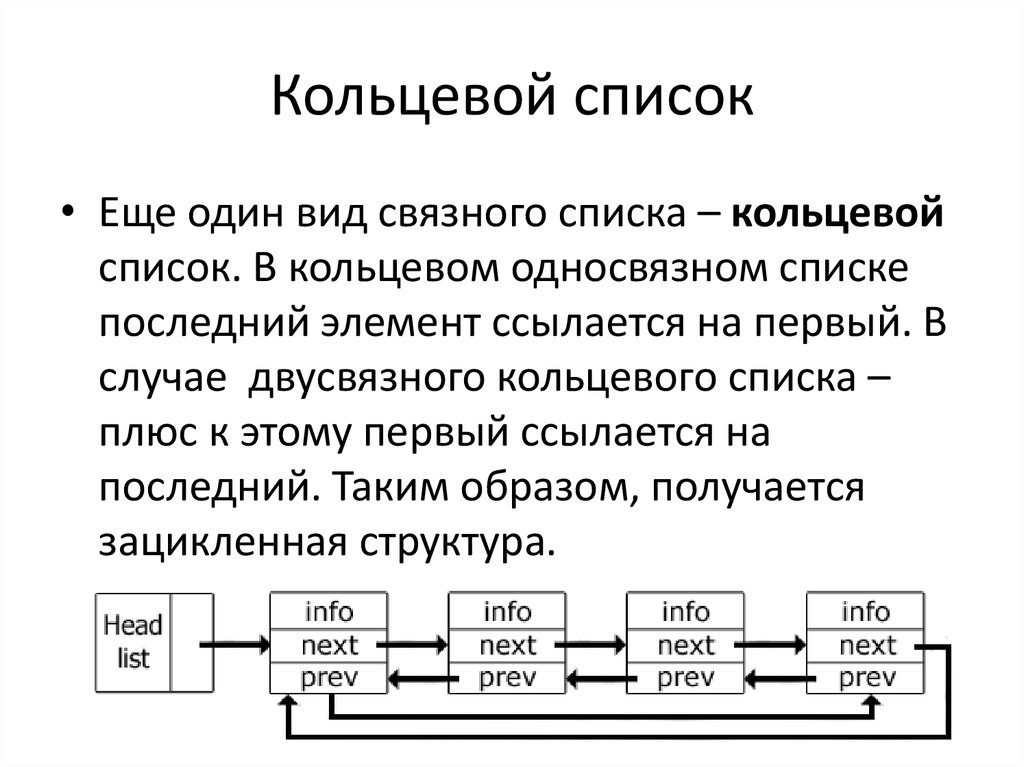 Чтобы перейти от одного узла к следующему в списке, в игру вступает свойство узла
Чтобы перейти от одного узла к следующему в списке, в игру вступает свойство узла self.next и возвращает ссылку на следующий узел. Подсчет узлов выполняется в цикле while до тех пор, пока мы не достигнем конца списка, который представлен ссылкой None на следующий узел.
Листинг 5: Класс Единого связанного списка (часть третья)
def list_length(self):
"returns the number of list items"
count = 0
current_node = self.head
while current_node is not None:
# increase counter by one
count = count + 1
# jump to the linked node
current_node = current_node. next
return count
next
return count
Метод output_list() выводит значения узлов с помощью свойства node data . Опять же, для перехода от одного узла к другому используется ссылка, предоставляемая через свойство next .
Листинг 6: Класс Single Linked List (часть четвертая)
def output_list(self):
"outputs the list (the value of the node, actually)"
current_node = self.head
while current_node is not None:
print(current_node.data)
# jump to the linked node
current_node = current_node.next
return
На основе класса SingleLinkedList мы можем создать правильный список с именем track и играть с его методами , как уже описано выше в Listings 3-6 . Поэтому мы создаем четыре узла списка, оцениваем их в цикле
Поэтому мы создаем четыре узла списка, оцениваем их в цикле for и выводим содержимое списка. Листинг 7 показывает, как это запрограммировать, а Листинг 8 показывает выходные данные.
Листинг 7: Создание узлов и вывод списка
# create four single nodes
node1 = ListNode(15)
node2 = ListNode(8.2)
item3 = "Berlin"
node4 = ListNode(15)
track = SingleLinkedList()
print("track length: %i" % track.list_length())
for current_item in [node1, node2, item3, node4]:
track.add_list_item(current_item)
print("track length: %i" % track.list_length())
track.output_list()
Вывод выглядит следующим образом и показывает, как растет список:
Листинг 8: Добавление узлов в список
$ python3 simple-list.py track length: 0 track length: 1 15 track length: 2 15 8.2 track length: 3 15 8.2 Berlin track length: 4 15 8.2 Berlin 15
Шаг 4: Поиск по списку
Поиск по всему списку осуществляется с помощью метода unordered_search() . Для поиска значения требуется дополнительный параметр. Глава списка-это отправная точка.
Во время поиска мы подсчитываем узлы. Чтобы указать совпадение, мы используем соответствующий номер узла. Метод unordered_search() возвращает список номеров узлов, представляющих совпадения. Например, и первый, и четвертый узел содержат значение 15. Поиск 15 результатов в списке с двумя элементами: [1, 4] .
Листинг 9: Метод поиска unordered_search()
def unordered_search (self, value):
"search the linked list for the node that has this value"
# define current_node
current_node = self. head
# define position
node_id = 1
# define list of results
results = []
while current_node is not None:
if current_node.has_value(value):
results.append(node_id)
# jump to the linked node
current_node = current_node.next
node_id = node_id + 1
return results
head
# define position
node_id = 1
# define list of results
results = []
while current_node is not None:
if current_node.has_value(value):
results.append(node_id)
# jump to the linked node
current_node = current_node.next
node_id = node_id + 1
return results
Шаг 5: Удаление элемента из списка
Удаление узла из списка требует корректировки только одной ссылки – та, которая указывает на удаляемый узел, теперь должна указывать на следующий. Эта ссылка хранится удаляемым узлом и должна быть заменена. В фоновом режиме сборщик мусора Python заботится о несвязанных объектах и приводит их в порядок.
Следующий метод называется remove_list_item_by_id() . В качестве параметра он ссылается на номер узла, аналогичный значению, возвращаемому функцией unordered_search() .
Листинг 10: Удаление узла по номеру узла
def remove_list_item_by_id(self, item_id):
"remove the list item with the item id"
current_id = 1
current_node = self. head
previous_node = None
while current_node is not None:
if current_id == item_id:
# if this is the first node (head)
if previous_node is not None:
previous_node.next = current_node.next
else:
self.head = current_node.next
# we don't have to look any further
return
# needed for the next iteration
previous_node = current_node
current_node = current_node.next
current_id = current_id + 1
return
head
previous_node = None
while current_node is not None:
if current_id == item_id:
# if this is the first node (head)
if previous_node is not None:
previous_node.next = current_node.next
else:
self.head = current_node.next
# we don't have to look any further
return
# needed for the next iteration
previous_node = current_node
current_node = current_node.next
current_id = current_id + 1
return
Шаг 6: Создание Двусвязного списка
Чтобы создать двусвязный список, естественно просто расширить класс ListNode , создав дополнительную ссылку на предыдущий узел. Это влияет на методы добавления, удаления и сортировки узлов. Как показано в Листинге 11 , для хранения ссылочного указателя на предыдущий узел в списке было добавлено новое свойство с именем previous . Мы изменим наши методы, чтобы использовать это свойство также для отслеживания и обхода узлов.
Мы изменим наши методы, чтобы использовать это свойство также для отслеживания и обхода узлов.
Листинг 11: Класс узлов расширенного списка
class ListNode:
def __init__(self, data):
"constructor class to initiate this object"
# store data
self.data = data
# store reference (next item)
self.next = None
# store reference (previous item)
self.previous = None
return
def has_value(self, value):
"method to compare the value with the node data"
if self.data == value:
return True
else:
return False
Теперь мы можем определить двусвязный список следующим образом:
Листинг 12: Класс Двойного Связанного списка
class DoubleLinkedList:
def __init__(self):
"constructor to initiate this object"
self. head = None
self.tail = None
return
def list_length(self):
"returns the number of list items"
count = 0
current_node = self.head
while current_node is not None:
# increase counter by one
count = count + 1
# jump to the linked node
current_node = current_node.next
return count
def output_list(self):
"outputs the list (the value of the node, actually)"
current_node = self.head
while current_node is not None:
print(current_node.data)
# jump to the linked node
current_node = current_node.next
return
def unordered_search (self, value):
"search the linked list for the node that has this value"
# define current_node
current_node = self.head
# define position
node_id = 1
# define list of results
results = []
while current_node is not None:
if current_node.
head = None
self.tail = None
return
def list_length(self):
"returns the number of list items"
count = 0
current_node = self.head
while current_node is not None:
# increase counter by one
count = count + 1
# jump to the linked node
current_node = current_node.next
return count
def output_list(self):
"outputs the list (the value of the node, actually)"
current_node = self.head
while current_node is not None:
print(current_node.data)
# jump to the linked node
current_node = current_node.next
return
def unordered_search (self, value):
"search the linked list for the node that has this value"
# define current_node
current_node = self.head
# define position
node_id = 1
# define list of results
results = []
while current_node is not None:
if current_node. has_value(value):
results.append(node_id)
# jump to the linked node
current_node = current_node.next
node_id = node_id + 1
return results
has_value(value):
results.append(node_id)
# jump to the linked node
current_node = current_node.next
node_id = node_id + 1
return results
Как было описано ранее, добавление узлов требует немного больше действий. Листинг 13 показывает, как это реализовать:
Листинг 13: Добавление узлов в двусвязный список
def add_list_item(self, item):
"add an item at the end of the list"
if isinstance(item, ListNode):
if self.head is None:
self.head = item
item.previous = None
item.next = None
self. tail = item
else:
self.tail.next = item
item.previous = self.tail
self.tail = item
return
tail = item
else:
self.tail.next = item
item.previous = self.tail
self.tail = item
return
При удалении элемента из списка необходимо учитывать аналогичные затраты. Листинг 14 показывает, как это сделать:
Листинг 14: Удаление элемента из двусвязного списка
def remove_list_item_by_id(self, item_id):
"remove the list item with the item id"
current_id = 1
current_node = self.head
while current_node is not None:
previous_node = current_node.previous
next_node = current_node.next
if current_id == item_id:
# if this is the first node (head)
if previous_node is not None:
previous_node. next = next_node
if next_node is not None:
next_node.previous = previous_node
else:
self.head = next_node
if next_node is not None:
next_node.previous = None
# we don't have to look any further
return
# needed for the next iteration
current_node = next_node
current_id = current_id + 1
return
next = next_node
if next_node is not None:
next_node.previous = previous_node
else:
self.head = next_node
if next_node is not None:
next_node.previous = None
# we don't have to look any further
return
# needed for the next iteration
current_node = next_node
current_id = current_id + 1
return
В листинге 15 показано, как использовать класс в программе Python.
Листинг 15: Построение двусвязного списка
# create three single nodes node1 = ListNode(15) node2 = ListNode(8.2) node3 = ListNode("Berlin") node4 = ListNode(15) track = DoubleLinkedList() print("track length: %i" % track.list_length()) for current_node in [node1, node2, node3, node4]: track.add_list_item(current_node) print("track length: %i" % track.list_length()) track.output_list() results = track.unordered_search(15) print(results) track.remove_list_item_by_id(4) track.output_list()
Как вы можете видеть, мы можем использовать класс точно так же, как и раньше, когда он был просто односвязным списком. Единственное изменение – это внутренняя структура данных.
Шаг 7: Создание Двусвязных списков с помощью deque
Поскольку другие инженеры столкнулись с той же проблемой, мы можем упростить вещи для себя и использовать одну из немногих существующих реализаций. В Python мы можем использовать объект deque из модуля collections . Согласно документации модуля:
Деки-это обобщение стеков и очередей (название произносится как “колода” и является сокращением от “двусторонняя очередь”). Deques поддерживают потокобезопасные, эффективные с точки зрения памяти приложения и всплывающие окна с обеих сторон deque с примерно одинаковой производительностью O(1) в любом направлении.
Deques поддерживают потокобезопасные, эффективные с точки зрения памяти приложения и всплывающие окна с обеих сторон deque с примерно одинаковой производительностью O(1) в любом направлении.
Например, этот объект содержит следующие методы:
append(): добавить элемент в правую часть списка (конец)append_left(): добавить элемент в левую часть списка (head)clear(): удалить все элементы из спискаcount(): подсчет количества элементов с определенным значениемcount(): подсчет количества элементов с определенным значениемcount(): подсчет количества элементов с определенным значениемpop(): удаление элемента из правой части списка (конец)pop left(): удаление элемента из левой части списка (head)remove(): удаление элемента из спискаreverse(): перевернуть список
Базовая структура данных deque представляет собой список Python, который является двусвязным. Первый узел списка имеет индекс 0. Использование
Первый узел списка имеет индекс 0. Использование deque приводит к значительному упрощению класса ListNode . Единственное, что мы сохраняем, – это переменная класса data для хранения значения узла. Листинг 16 выглядит следующим образом:
Листинг 16: Класс ListNode с deque (упрощенный)
from collections import deque
class ListNode:
def __init__(self, data):
"constructor class to initiate this object"
# store data
self.data = data
return
Определение узлов не меняется и аналогично Листингу 2 . С учетом этих знаний мы создаем список узлов следующим образом:
Листинг 17: Создание списка с помощью deque
track = deque([node1, node2, node3])
print("three items (initial list):")
for item in track:
print(item. data)
data)
Добавление элемента в начало списка работает с помощью метода append_left() как показано в листинге 18 :
Листинг 18: Добавление элемента в начало списка
# add an item at the beginning
node4 = ListNode(15)
track.append_left(node4)
print("four items (added as the head):")
for item in track:
print(item.data)
Аналогично, append() добавляет узел в конец списка, как показано в Листинге 19 :
Листинг 19: Добавление элемента в конец списка
# add an item at the end
node5 = ListNode("Moscow")
print("five items (added at the end):")
track. append(node5)
for item in track:
print(item.data)
append(node5)
for item in track:
print(item.data)
Вывод
Связанные списки как структуры данных просты в реализации и обеспечивают большую гибкость использования. Это делается с помощью нескольких строк кода. В качестве улучшения вы можете добавить счетчик узлов – переменную класса, которая просто содержит количество узлов в списке. Это уменьшает определение длины списка до одной операции с O(1), и вам не нужно проходить весь список.
Для дальнейшего чтения и альтернативных реализаций вы можете посмотреть здесь:
Признание
Автор хотел бы поблагодарить Герольда Рупрехта и Мэнди Ноймайер за их поддержку и комментарии при подготовке этой статьи.
что это такое и как его реализовать
Давайте поговорим немного о связных списках. Вероятно, вы о них слышали. Скажем, на лекциях по структурам данных. И возможно, вы думали, что это как-то сильно заумно. Почему бы не использовать массив? На самом деле связные списки имеют некоторые преимущества перед массивами и простыми списками. Поначалу эта тема может показаться сложной, но не волнуйтесь: мы все разберем.
Поначалу эта тема может показаться сложной, но не волнуйтесь: мы все разберем.
Если вы представите себе фотографию людей, взявшихся за руки в хороводе, вы получите примерное представление о такой структуре, как связный список. Это некоторое количество отдельных узлов, связанных между собой ссылками, т. е. ссылками на другие узлы. Связные списки бывают двух видов: однонаправленные и двунаправленные (односвязные и двусвязные).
Источник: Medium.comВ односвязных списках каждый узел имеет одну стрелку, указывающую вперед, а в двусвязных узлы имеют еще и стрелки, указывающие назад. Но на собеседованиях в вопросах, касающихся связных списков, чаще всего имеются в виду односвязные. Почему? Их проще реализовать. Да, у вас не будет возможности перемещаться по списку в обратном направлении, но для отслеживания узлов хватит и однонаправленных связей.
Давайте попробуем реализовать связный список на Python. Возможно, вы бы начали с class Linked_list, а затем создали в нем узлы, но все можно сделать куда проще. Представьте цепочку из скрепок. Мы берем кучку скрепок и соединяем их, цепляя друг за дружку.
Представьте цепочку из скрепок. Мы берем кучку скрепок и соединяем их, цепляя друг за дружку.
Цепочку создают отдельные скрепки плюс тот факт, что они сцеплены между собой. Поэтому вместо создания класса Linked_list мы просто создадим класс Node и позволим отдельным узлам связываться друг с другом.
class Node:
Далее, как обычно при создании класса на Python, мы создаем метод __init__. Этот метод инициализирует все поля, например, переменные в классе, при создании каждого нового объекта Node.
Мы будем принимать переменную data — это значение, которое мы хотим сохранять в узле. Также нам нужно определить ссылку, направленную вперед, она традиционно называется next. Сначала узел не связан ни с чем, поэтому мы устанавливаем next в None.
class Node:
def __init__(self, data):
self. data = data
self.next = None
data = data
self.next = NoneЭто почти все, что нам нужно. Можно оставить, как есть, но в книге «Cracking the Coding Interview» также реализуется метод appendToTail(), который создает новый узел и добавляет его в конец списка, проходя его, так что нам не приходится делать это вручную.
Начнем с определения этого метода в классе Node. Метод будет принимать значение, которое мы хотим поместить в новый узел, и ключевое слово self (это специфично для Python).
class Node:
def __init__(self, data):
self.data = data
self.next = None
def append(self, val):
passПервое, что мы делаем, это создаем новый узел с заданным значением. Назовем его end.
def append(self, val):
end = Node(val)Затем мы создаем указатель (поинтер). Это может звучать слишком технически, но по сути мы создаем ссылку на головной элемент (
Это может звучать слишком технически, но по сути мы создаем ссылку на головной элемент (head) нашего списка. Мы делаем так, потому что хотим проходить по списку, не переназначая в нем ничего. Итак, мы делаем ссылку на первый узел, self, и сохраняем его в переменной n.
def append(self, val):
end = Node(val)
n = selfНаконец, мы проходим список. Как мы это делаем? Нам нужно всего лишь перемещаться к следующему узлу, если он есть. А если следующего узла нет, мы поймем, что мы уже в конце списка. Для прохождения списка до предпоследнего узла мы используем простой цикл while.
def append(self, val):
end = Node(val)
n = self
while (n. next):
n = n.next
next):
n = n.nextНаконец, мы указываем на последний узел, за которым нет следующего узла. Мы просто берем end — наш новый узел — и устанавливаем n.next = end.
def append(self, val):
end = Node(val)
n = self
while (n.next):
n = n.next
n.next = endВот и все! Вот как выглядит наш класс полностью:
list_node.py
class Node:
def __init__(self, data):
self.next = None
self.data = data
def append(self, val):
end = Node(val)
n = self
while (n.next):
n = n.next
n. next = end
next = endПроверяем наш связный список
Давайте все это проверим. Начнем с создания нового объекта Node. Назовем его ll (две латинские буквы «l» в нижнем регистре как сокращение Linked List). Назначим ему значение 1.
ll = Node(1)
Поскольку мы написали такой классный метод append(), мы можем вызывать его для добавления в наш список новых узлов.
ll.append(2) ll.append(3)
Как нам увидеть, как выглядит наш список? Теоретически, выглядеть он должен следующим образом:
[1] --> [2] --> [3]
Но нет способа вывести его именно в таком виде. Нам нужно пройти список, выводя каждое значение. Вы же помните, как проходить список? Мы только что это делали. Повторим:
- Создаем переменную, указывающую на
head. - Если есть следующий узел, перемещаемся к этому узлу.
И просто выводим data в каждом узле. Мы начинаем с шага № 1: создаем новую переменную и назначаем ее головным элементом списка.
node = ll
Далее мы выводим первый узел. Почему мы не начали с цикла while? Цикл while проитерируется только дважды, потому что только у двух узлов есть next (у последнего узла его нет). В информатике это называется ошибкой на единицу (когда нужно сделать что-то Х раз плюс 1). Это можно представить в виде забора. Вы ставите столб, затем секцию забора, и чередуете пару столб + секция столько раз, сколько нужно по длине.
Но вы не можете оставить последнюю секцию забора висящей в воздухе. Ограда должна закончиться столбом, а не секцией. Поэтому вам приходится либо добавлять еще один столб в конце, либо (что в информатике более распространено) начать с постановки столба, а затем добавлять пары секция + столб. Это мы и сделаем.
Для начала мы выведем первый узел, а затем запустим цикл while для вывода всех последующих узлов.
node = ll print(node.data) while node.next: node = node.next print(node.data)
Запустив это для нашего предыдущего списка, мы получим в консоли:
1 2 3
Ура! Наш связный список работает.
Зачем уметь создавать связный список на Python?
Зачем вообще может понадобиться создавать собственный связный список на Python? Это хороший вопрос. Использование связных списков имеет некоторые преимущества по сравнению с использованием просто списков Python.
Традиционно вопрос звучит как «чем использование связного списка лучше использования массива». Основная идея в том, что массивы в Java и других ООП-языках имеют фиксированный размер, поэтому для добавления элемента приходится создавать новый массив с размером N + 1 и помещать в него все значения из предыдущего массива. Пространственная и временная сложность этой операции — O(N). А вот добавление элемента в конец связного списка имеет постоянную временную сложность (O(1)).
Списки в Python это не настоящие массивы, а скорее реализация динамического массива, что имеет свои преимущества и недостатки. В Википедии есть таблица со сравнением производительности связных списков, массивов и динамических массивов.
В Википедии есть таблица со сравнением производительности связных списков, массивов и динамических массивов.
Если вопрос производительности вас не тревожит, тогда да, проще реализовать обычный список Python. Но научиться реализовывать собственный связный список все равно полезно. Это как изучение математики: у нас есть калькуляторы, но основные концепции мы все-таки изучаем.
В сообществе разработчиков постоянно ведутся горячие споры о том, насколько целесообразно давать на технических интервью задания, связанные с алгоритмами и структурами данных. Возможно, в этом и нет никакого смысла, но на собеседовании вас вполне могут попросить реализовать связный список на Python. И теперь вы знаете, как это сделать.
Связанные списки в деталях с примерами Python: одинарные связанные списки
Связанные списки — одна из наиболее часто используемых структур данных в
любом языке программирования. В этой статье мы подробно изучим связанные
списки. Мы увидим, какие существуют типы связанных списков, как
перемещаться по связанному списку, как вставлять и удалять элементы из
связанного списка, каковы различные методы сортировки связанного списка,
как перевернуть связанный список и т. Д. .
Д. .
Прочитав эту статью, вы сможете взломать все вопросы собеседования по связному списку.
Что такое связанный список?
Прежде чем мы изучим, что такое связанные списки, давайте сначала кратко рассмотрим, как массивы хранят данные. В массивах данные хранятся в непрерывных ячейках памяти. Например, если первый элемент в массиве хранится в индексе 10 памяти и имеет размер 15 байт, второй элемент будет сохранен в индексе 10 + 15 + 1 = 26-й индекс. Следовательно, можно легко пройти по массиву.
Чтобы найти третий элемент в массиве, вы можете просто использовать начальный индекс первого элемента плюс размер первого элемента плюс размер второго элемента плюс 1.
Как связанные списки хранят данные
Связанные списки, с другой стороны, разные. Связанные списки не хранят
данные в непрерывных ячейках памяти. Для каждого элемента в ячейке
памяти связанный список хранит значение элемента и ссылку или указатель
на следующий элемент. Одна пара элемента связанного списка и ссылка на
следующий элемент составляет узел.
Например, если узел состоит из 34 | 10, это означает, что значение узла равно 30, а следующий элемент сохраняется в ячейке памяти «10». Чтобы пройти по связанному списку, вам просто нужно знать местоположение в памяти или ссылку на первый узел, остальные узлы могут быть последовательно перемещены, используя ссылку на следующий элемент в каждом узле.
Ссылка на первый узел также известна как начальный узел.
Связанные списки и массивы:
- Связанный список — это динамическая структура данных, что означает,
что память, зарезервированная для списка ссылок, может быть
увеличена или уменьшена во время выполнения. Память для структуры
данных связанного списка заранее не выделяется. Всякий раз, когда
требуется добавить новый элемент в связанный, память для нового узла
создается во время выполнения. С другой стороны, в случае массива
память должна быть выделена заранее для определенного количества
элементов. В случаях, когда недостаточно элементов для заполнения
всего индекса массива, память тратится впустую.

- Поскольку для массивов требуются непрерывные ячейки памяти, очень сложно удалить или вставить элемент в массив, так как ячейки памяти большого количества элементов должны быть обновлены. С другой стороны, элементы связанного списка не хранятся в непрерывной области памяти, поэтому вы можете легко обновить связанные списки.
- Благодаря своей гибкости связанный список больше подходит для реализации таких структур данных, как стеки, очереди и списки.
Однако у связанного списка есть и недостатки.
- Поскольку каждый элемент связанного списка должен хранить ссылку на следующий элемент, требуется дополнительная память.
- В отличие от массивов, где вы можете получить прямой доступ к элементу, вы не можете напрямую получить доступ к элементу связанного списка, поскольку единственная информация, которую вы имеете, — это ссылка на первый элемент. В терминах Big O время доступа в наихудшем случае — O (n).
В этой серии статей мы изучим следующие типы связанных списков, а также
их различные функции.
- Единый связанный список
- Двусвязный список
- Циркулярный связанный список
- Связанный список с заголовком
- Отсортированный связанный список
В этой первой части статьи мы сосредоточимся на едином связном списке и его различных операциях.
Единый связанный список
Создание класса узла
Создание класса единого связанного
списка
Обход элементов связанного списка
Вставка элементов
Подсчет элементов
Поиск элементов
Создание связного списка
Удаление элементов
Обращение связного списка
Единый связанный список
Единый связанный список — самый простой из всех вариантов связанных списков. Каждый узел в едином связанном списке содержит элемент и ссылку на следующий элемент, и все.
В этом разделе мы увидим, как создать узел для единого связанного списка вместе с функциями для различных типов вставки, обхода и удаления.
Создание класса узла
Первое, что вам нужно сделать, это создать класс для узлов. Объекты
этого класса будут фактическими узлами, которые мы вставим в наш
связанный список. Мы знаем, что узел для единственного связанного списка
содержит элемент и ссылку на следующий узел. Следовательно, наш класс
узла будет содержать две переменные-члены:
Объекты
этого класса будут фактическими узлами, которые мы вставим в наш
связанный список. Мы знаем, что узел для единственного связанного списка
содержит элемент и ссылку на следующий узел. Следовательно, наш класс
узла будет содержать две переменные-члены: item и ref . Значение item будет установлено значением, переданным через конструктор, в то
время как ссылка будет изначально установлена на null.
Выполните следующий скрипт:
class Node: def __init__(self, data): self.item = data self.ref = None
Создание класса единого связанного списка
Затем нам нужно создать класс для связанного списка. Этот класс будет
содержать методы для вставки, удаления, обхода и сортировки списка.
Первоначально класс будет содержать только один член start_node который будет указывать на начальный или первый узел списка. Значение start_node будет установлено равным null с помощью конструктора,
поскольку связанный список будет пуст во время создания. Следующий
сценарий создает класс для связанного списка.
Следующий
сценарий создает класс для связанного списка.
class LinkedList: def __init__(self): self.start_node = None
Теперь мы создали класс для нашего единственного списка. Следующим шагом является добавление функции вставки для вставки элементов в связанный список. Но перед этим мы добавим функцию для просмотра связанного списка. Эта функция поможет нам прочитать данные в нашем списке.
Просмотр элементов связанного списка
Код Python для функции перемещения выглядит следующим образом. Добавьте
приведенную ниже функцию в LinkedList который мы создали в предыдущем
разделе.
def traverse_list(self):
if self.start_node is None:
print("List has no element")
return
else:
n = self.start_node
while n is not None:
print(n.item , " ")
n = n.ref
Посмотрим, что происходит в приведенной выше функции. Функция состоит из двух основных частей. Во-первых, он проверяет, пуст ли связанный список. Следующий код проверяет это:
if self.start_node is None: print("List has no element") return
Если связанный список пуст, это означает, что нет элемента для
повторения. В таких случаях traverse_list() просто выводит утверждение
о том, что в списке нет элементов.
В противном случае, если в списке есть элемент, будет выполнен следующий фрагмент кода:
n = self.start_node while n is not None: print(n.item , " ") n = n.ref
Как мы уже говорили ранее, start будет содержать ссылку на первые
узлы. Поэтому мы инициализируем переменную n с start . Затем мы
выполняем цикл, который выполняется до тех пор, пока n станет равным
нулю. Внутри цикла мы печатаем элемент, хранящийся в текущем узле, а
затем устанавливаем значение переменной n n.ref , которое содержит
ссылку на следующий узел. Ссылка на последний узел — None поскольку
после этого узла нет. Следовательно, когда n становится None , цикл
завершается.
Теперь у нас есть функция для обхода связанного списка, давайте посмотрим, как мы можем добавлять элементы в один связанный список.
Вставка предметов
В зависимости от места, куда вы хотите вставить элемент, существуют разные способы вставки элементов в один связанный список.
Вставка элементов в начале
Самый простой способ вставить элемент в один связанный список — это
добавить элемент в начало списка. Следующая функция вставляет элемент в
начало списка. Добавьте эту функцию в созданный нами ранее класс LinkedList
def insert_at_start(self, data): new_node = Node(data) new_node.ref = self.start_node self.start_node= new_node
В приведенном выше скрипте мы создаем метод insert_at_start() , метод
принимает один параметр, который в основном является значением элемента,
который мы хотим вставить. Внутри метода мы просто создаем объект Node и устанавливаем его ссылку на start_node поскольку start_node ранее
хранил первый узел, который после вставки нового узла в начало станет
вторым узлом.
Поэтому мы добавляем ссылку на start_node в ref нового узла. Теперь
, так как new_node является первым узлом, мы устанавливаем значение start_node переменной в new_node .
Вставка элементов в конец
Следующая функция используется для добавления элемента в конец связанного списка.
def insert_at_end(self, data): new_node = Node(data) if self.start_node is None: self.start_node = new_node return n = self.start_node while n.ref is not None: n= n.ref n.ref = new_node;
В приведенном выше скрипте мы создаем функцию insert_at_end() ,
которая вставляет элемент в конец связанного списка. Значение элемента,
который мы хотим вставить, передается в качестве аргумента функции.
Функция состоит из двух частей. Сначала мы проверяем , если связанный
список пуст или нет, если связанный список пуст, все , что мы должны
сделать , это установить значение start_node переменной в new_node объекта.
С другой стороны, если список уже содержит какие-то узлы. Мы
инициализируем переменную n с помощью начального узла. Затем мы
перебираем все узлы в списке, используя цикл while, как мы это делали в
случае функции traverse_list Цикл завершается, когда мы достигаем
последнего узла. Затем мы устанавливаем ссылку последнего узла на вновь
созданный new_node .
Добавьте insert_at_end() в класс LinkedList
Вставка элемента после другого элемента
Возможно, нам потребуется добавить элемент после другого элемента в один
связанный список. Для этого мы можем использовать insert_after_item() как определено ниже:
def insert_after_item(self, x, data):
n = self.start_node
print(n.ref)
while n is not None:
if n.item == x:
break
n = n.ref
if n is None:
print("item not in the list")
else:
new_node = Node(data)
new_node.ref = n.ref
n.ref = new_node
Функция insert_after_item() принимает два параметра: x и data . Первый параметр — это элемент, после которого вы хотите вставить новый
узел, а второй параметр содержит значение для нового узла.
Первый параметр — это элемент, после которого вы хотите вставить новый
узел, а второй параметр содержит значение для нового узла.
Начнем с создания новой переменной n и присвоения start_node переменной start_node. Затем мы просматриваем связанный список,
используя цикл while. Цикл while выполняется до тех пор, пока n станет None . Во время каждой итерации мы проверяем, равно ли значение,
хранящееся в текущем узле, значению, переданному параметром x Если
сравнение вернет истину, мы прервем цикл.
Затем, если элемент найден, n не будет None . Ссылка new_node устанавливается на ссылку, сохраненную n а ссылка n устанавливается
на new_node . Добавьте insert_after_item() в класс LinkesList
Вставка элемента перед другим элементом
def insert_before_item(self, x, data):
if self.start_node is None:
print("List has no element")
return
if x == self. start_node.item:
new_node = Node(data)
new_node.ref = self.start_node
self.start_node = new_node
return
n = self.start_node
print(n.ref)
while n.ref is not None:
if n.ref.item == x:
break
n = n.ref
if n.ref is None:
print("item not in the list")
else:
new_node = Node(data)
new_node.ref = n.ref
n.ref = new_node
start_node.item:
new_node = Node(data)
new_node.ref = self.start_node
self.start_node = new_node
return
n = self.start_node
print(n.ref)
while n.ref is not None:
if n.ref.item == x:
break
n = n.ref
if n.ref is None:
print("item not in the list")
else:
new_node = Node(data)
new_node.ref = n.ref
n.ref = new_node
В приведенном выше скрипте мы определяем insert_before_item() .
Функция состоит из трех частей. Давайте подробно рассмотрим каждую
часть.
if self.start_node is None:
print("List has no element")
return
В приведенном выше скрипте мы проверяем, пуст ли список. Если он действительно пуст, мы просто печатаем, что в списке нет элемента, и возвращаемся из функции.
Затем мы проверяем, находится ли элемент по первому индексу. Взгляните на следующий сценарий:
if x == self.start_node.item: new_node = Node(data) new_node.ref = self.start_node self.start_node = new_node return
Если элемент, после которого мы хотим вставить новый узел, находится в
первом index. Мы просто устанавливаем ссылку на вновь вставленный узел
на
Мы просто устанавливаем ссылку на вновь вставленный узел
на start_node а затем устанавливаем значение start_node на new_node .
Наконец, если список не равен None и элемент не найден по первому
индексу, мы создаем новую переменную n и присваиваем start_node переменную start_node. Затем мы просматриваем связанный список,
используя цикл while. Цикл while выполняется до n.ref станет None .
Во время каждой итерации мы проверяем, равно ли значение, хранящееся в
ссылке текущего узла, значению, переданному параметром x Если
сравнение вернет истину, мы прервем цикл.
Затем, если элемент найден, n.ref не будет None . Ссылка new_node устанавливается на ссылку n а ссылка n устанавливается на new_node . Взгляните на следующий сценарий:
if n.ref is None:
print("item not in the list")
else:
new_node = Node(data)
new_node. ref = n.ref
n.ref = new_node
ref = n.ref
n.ref = new_node
Добавьте insert_before_item() в класс LinkedList
Вставка элемента по определенному индексу
Иногда нам нужно вставить элемент по определенному индексу, мы можем сделать это с помощью следующего скрипта:
def insert_at_index (self, index, data):
if index == 1:
new_node = Node(data)
new_node.ref = self.start_node
self.start_node = new_node
i = 1
n = self.start_node
while i < index-1 and n is not None:
n = n.ref
i = i+1
if n is None:
print("Index out of bound")
else:
new_node = Node(data)
new_node.ref = n.ref
n.ref = new_node
В скрипте мы сначала проверяем, равен ли индекс, в котором мы хотим
сохранить элемент, 1, затем просто назначаем start_node ссылке на new_node а затем устанавливаем значение start_node на new_node .
Затем выполните цикл while, который выполняется до тех пор, пока счетчик i станет больше или равным index-1 . Например, если вы хотите
добавить новый узел в третий index. Во время первой итерации цикла while
Например, если вы хотите
добавить новый узел в третий index. Во время первой итерации цикла while i станет равным 2, а текущий итерируемый узел будет равен «2». Цикл не
будет выполняться снова, поскольку i равно 2, что равно index-1 (3-1 =
2). Следовательно, петля разорвется. Затем мы добавляем новый узел после
текущего итеративного узла (который является узлом 2), следовательно,
новый узел добавляется по индексу.
Важно отметить, что если индекс или местоположение, переданное в качестве аргумента, больше, чем размер связанного списка, пользователю будет отображаться сообщение о том, что индекс находится вне диапазона или вне диапазона.
Тестирование функций вставки
Теперь мы определили все наши функции вставки, давайте протестируем их.
Сначала создайте объект класса связанного списка следующим образом:
new_linked_list = LinkedList()
Затем давайте сначала insert_at_end() чтобы добавить три элемента в
связанный список. Выполните следующий скрипт:
Выполните следующий скрипт:
new_linked_list.insert_at_end(5) new_linked_list.insert_at_end(10) new_linked_list.insert_at_end(15)
Чтобы увидеть, действительно ли элементы были вставлены, давайте пройдемся по связанному списку, используя функцию обхода.
new_linked_list.traverse_list()
Вы должны увидеть следующий результат:
5 10 15
Затем давайте добавим элемент в начало:
new_linked_list.insert_at_start(20)
Теперь, если вы пройдете по списку, вы должны увидеть следующий вывод:
20 5 10 15
Добавим после пункта 10 новый элемент 17:
new_linked_list.insert_after_item(10, 17)
Теперь при обходе списка возвращается следующий результат:
20 5 10 17 15
Вы можете увидеть 17 вставленных после 10.
Давайте теперь вставим еще один элемент 25 перед элементом 17, используя insert_before_item() как показано ниже:
new_linked_list.insert_before_item(17, 25)
Теперь список будет содержать следующие элементы:
20 5 10 25 17 15
Наконец, давайте добавим элемент в третье место, которое в настоящее
время занято 10. Вы увидите, что 10 переместит на одно место вперед, и
новый элемент будет вставлен на его место. Для этого можно использовать
функцию insert_at_index() Следующий скрипт вставляет элемент 8 в
третий индекс списка.
new_linked_list.insert_at_index(3,8)
Теперь, если вы пройдете по списку, вы должны увидеть следующий вывод:
20 5 8 10 25 17 15
И с этим мы протестировали все наши функции вставки. В настоящее время в нашем списке 7 элементов. Напишем функцию, которая возвращает количество элементов в связанном списке.
Подсчет элементов
Следующая функция подсчитывает общее количество элементов.
def get_count(self): if self.start_node is None: return 0; n = self.start_node count = 0; while n is not None: count = count + 1 n = n.ref return count
В приведенном выше скрипте мы создаем get_count() которая просто
подсчитывает количество элементов в связанном списке. Функция просто
проходит через все узлы в массиве и увеличивает счетчик, используя цикл
while. В конце цикла счетчик содержит общее количество элементов в
цикле.
LinkedList выше функцию в класс LinkedList, скомпилируйте LinkedList и затем вставьте некоторые элементы в LinkedList как мы это делали в
предыдущем разделе. К концу последнего раздела у нас было 7 элементов в
нашем связанном списке.
Давайте воспользуемся get_count() чтобы получить общее количество
элементов в списке:
new_linked_list.get_count()
На выходе вы должны увидеть количество элементов в связанном списке.
В качестве альтернативы, другой способ получить «счетчик» списка — это
отслеживать количество элементов, вставленных и удаленных из списка, в
простой переменной счетчика, принадлежащей классу LinkedList Это
работает хорошо и быстрее, чем get_count выше, если базовая структура
данных списка не может управляться извне класса.
Поиск элементов
Поиск элемента очень похож на подсчет или обход связанного списка, все, что вам нужно сделать, — это сравнить значение, которое нужно найти, со значением узла во время каждой итерации. Если значение найдено, выведите, что значение найдено, и прервите цикл. Если элемент не найден после обхода всех узлов, просто выведите, что элемент не найден.
Скрипт для search_item() выглядит следующим образом:
def search_item(self, x):
if self.start_node is None:
print("List has no elements")
return
n = self.start_node
while n is not None:
if n.item == x:
print("Item found")
return True
n = n.ref
print("item not found")
return False
LinkedList выше функцию в класс LinkedList. Выполним поиск элемента в
ранее созданном списке. Выполните следующий скрипт:
new_linked_list.search_item(5)
Поскольку мы вставили 5 в наш связанный список, вышеуказанная функция вернет true. Результат будет выглядеть так:
Item found True
Создание связанного списка
Хотя мы можем добавлять элементы по одному, используя любую из функций
вставки. Давайте создадим функцию, которая просит пользователя ввести
количество элементов в узле, а затем в отдельный элемент, и вводит этот
элемент в связанный список.
Давайте создадим функцию, которая просит пользователя ввести
количество элементов в узле, а затем в отдельный элемент, и вводит этот
элемент в связанный список.
def make_new_list(self):
nums = int(input("How many nodes do you want to create: "))
if nums == 0:
return
for i in range(nums):
value = int(input("Enter the value for the node:"))
self.insert_at_end(value)
В приведенном выше сценарии make_new_list() сначала запрашивает у
пользователя количество элементов в списке. Затем, используя цикл for,
пользователю предлагается ввести значение для каждого узла, которое
затем вставляется в связанный список с помощью функции insert_at_end() .
На следующем make_new_list() в действии.
{.ezlazyload .img-responsive}
Удаление элементов
В этом разделе мы увидим различные способы удаления элемента из единого связанного списка.
Удаление с самого начала
Удалить элемент или элемент из начала связанного списка очень просто. Мы
должны установить ссылку
Мы
должны установить ссылку start_node на второй узел, что мы можем
сделать, просто присвоив значение ссылки начального узла (который
указывает на второй узел) начальному узлу, как показано ниже:
def delete_at_start(self):
if self.start_node is None:
print("The list has no element to delete")
return
self.start_node = self.start_node.ref
В приведенном выше сценарии мы сначала проверяем, пуст список или нет.
Если список пуст, мы отображаем сообщение о том, что в списке нет
элемента для удаления. В противном случае мы присваиваем значение start_node.ref start_node . start_node теперь будет указывать на
второй элемент. Добавьте delete_at_start() в класс LinkedList
Удаление в конце
Чтобы удалить элемент из конца списка, нам просто нужно перебрать
связанный список до второго последнего элемента, а затем нам нужно
установить ссылку на второй последний элемент на none, что преобразует
второй последний элемент в последний элемент.
Скрипт для функции delete_at_end выглядит следующим образом:
def delete_at_end(self):
if self.start_node is None:
print("The list has no element to delete")
return
n = self.start_node
while n.ref.ref is not None:
n = n.ref
n.ref = None
Добавьте приведенный выше сценарий в класс LinkedList()
Удаление по значению элемента
Чтобы удалить элемент по значению, мы сначала должны найти узел, содержащий элемент с указанным значением, а затем удалить узел. Поиск элемента с указанным значением очень похож на поиск элемента. Как только удаляемый элемент найден, ссылка на узел перед этим элементом устанавливается на узел, который существует после удаляемого элемента. Взгляните на следующий сценарий:
def delete_element_by_value(self, x):
if self.start_node is None:
print("The list has no element to delete")
return
# Deleting first node
if self.start_node.item == x:
self.start_node = self.start_node. ref
return
n = self.start_node
while n.ref is not None:
if n.ref.item == x:
break
n = n.ref
if n.ref is None:
print("item not found in the list")
else:
n.ref = n.ref.ref
ref
return
n = self.start_node
while n.ref is not None:
if n.ref.item == x:
break
n = n.ref
if n.ref is None:
print("item not found in the list")
else:
n.ref = n.ref.ref
В приведенном выше сценарии мы сначала проверяем, пуст ли список. Затем мы проверяем, находится ли удаляемый элемент в начале связанного списка. Если элемент найден в начале, мы удаляем его, устанавливая первый узел на ссылку первого узла (который в основном относится ко второму узлу).
Наконец, если элемент не найден по первому индексу, мы перебираем связанный список и проверяем, равно ли значение повторяемого узла значению, которое нужно удалить. Если сравнение возвращает истину, мы устанавливаем ссылку предыдущего узла на узел, который существует после удаляемого узла.
Тестирование функций удаления
Давайте протестируем функции удаления, которые мы только что создали. Но перед этим добавьте фиктивные данные в наш связанный список, используя следующий скрипт:
new_linked_list.insert_at_end(10) new_linked_list.insert_at_end(20) new_linked_list.insert_at_end(30) new_linked_list.insert_at_end(40) new_linked_list.insert_at_end(50)
Приведенный выше сценарий вставляет 5 элементов в связанный список. Если вы пройдете по списку, вы должны увидеть следующие элементы:
10 20 30 40 50
Давайте сначала удалим элемент с самого начала:
new_linked_list.delete_at_start()
Теперь, если вы пройдете по списку, вы должны увидеть следующий вывод:
20 30 40 50
Теперь удалим элемент с конца:
new_linked_list.delete_at_end()
Список теперь содержит следующие элементы:
20 30 40
Наконец, давайте удалим элемент по значению, скажем 30.
new_linked_list.delete_element_by_value(30)
Теперь, если вы пройдете по списку, вы не должны увидеть элемент 30.
Переворачивание связного списка
Чтобы перевернуть связанный список, вам нужно иметь три переменные: prev , n и next .
prev отследит предыдущий узел, то next будет
отслеживать следующий узел будет ли n будет соответствовать текущему
узлу.
Мы запускаем цикл while, присваивая начальный узел переменной n а prev не инициализируется значением none. Цикл выполняется до тех пор,
пока n станет равным нулю. Внутри цикла while вам необходимо выполнить
следующие функции.
- Присвойте значение ссылки текущего узла
next. - Установите значение ссылки текущего узла
nнаprev - Установите
prevна текущий узелn. - Установите текущий узел
nна значениеnextузла.
В конце цикла prev будет указывать на последний узел, нам нужно
сделать его первым узлом, поэтому мы устанавливаем значение переменной self.start_node prev . Цикл while заставит каждый узел указывать на
его предыдущий узел, в результате чего будет получен обратный связанный
список. Сценарий выглядит следующим образом:
Сценарий выглядит следующим образом:
def reverse_linkedlist(self): prev = None n = self.start_node while n is not None: next = n.ref n.ref = prev prev = n n = next self.start_node = prev
LinkedList выше функцию в класс LinkedList. Создайте связанный список
случайных чисел, а затем посмотрите, можно ли его отменить, используя
функцию reverse_linkedlist()
Заключение
В этой статье мы начали обсуждение единого связного списка. Мы увидели, какие различные функции могут выполняться в связанном списке, такие как переход по связному списку, вставка элементов в связанный список, поиск и подсчет элементов связанного списка, удаление элементов из связанного списка и реверсирование единственного связанного списка.
Это первая часть серии статей о связанном списке. В следующей части ( скоро ) мы увидим, как отсортировать единый связанный список, как
объединить отсортированные связанные списки и как удалить циклы из
единого связанного списка.
Глава 3. Связные списки, стеки и очереди. Фундаментальные алгоритмы и структуры данных в Delphi
Глава 3. Связные списки, стеки и очереди. Фундаментальные алгоритмы и структуры данных в DelphiВикиЧтение
Фундаментальные алгоритмы и структуры данных в Delphi
Бакнелл Джулиан М.
Содержание
Глава 3. Связные списки, стеки и очереди
Как и массивы, связные списки представляют собой универсальную структуру данных, широко используемую многими программистами. Однако, в отличие от массивов, связные списки не входят в состав стандартного языка Object Pascal. Тем не менее, в Object Pascal создать связный список достаточно просто. Все что для этого нужно — наличие в составе языка указателя, хотя фактически могут использоваться и классы или объекты.
На основе связных списков можно легко организовать стеки и очереди — еще две простые, но эффективные структуры данных. Несмотря на то что они, на первый взгляд, не имеют ничего общего со связными списками, их можно написать на базе односвязных списков. И, как мы увидим чуть позже, иногда удобнее реализовать стеки и очереди на базе массивов, а не связных списков.
Несмотря на то что они, на первый взгляд, не имеют ничего общего со связными списками, их можно написать на базе односвязных списков. И, как мы увидим чуть позже, иногда удобнее реализовать стеки и очереди на базе массивов, а не связных списков.
Начнем наше рассмотрение со связного списка и операций, которые такой список должен поддерживать.
Глава 3 Альтернативные стеки протоколов
Глава 3 Альтернативные стеки протоколов Компьютерная программа — идеальный инструмент для решения тех задач, которые предполагают скрупулезное следование предписаниям. В ситуациях, не предусмотренных инструкциями, компьютер становится практически беспомощным.
I.3.1 Протоколы, элементы, стеки и наборы
I.3.1 Протоколы, элементы, стеки и наборы
Протоколом (protocol) называется набор правил для одной из коммуникационных функций. Например, протокол IP представляет собой набор правил для маршрутизации данных, a TCP определяет правила для надежной и последовательной доставки
Например, протокол IP представляет собой набор правил для маршрутизации данных, a TCP определяет правила для надежной и последовательной доставки
ГЛАВА 5 Очереди сообщений Posix
ГЛАВА 5 Очереди сообщений Posix 5.1. Введение Очередь сообщений можно рассматривать как связный список сообщений. Программные потоки с соответствующими разрешениями могут помещать сообщения в очередь, а потоки с другими соответствующими разрешениями могут извлекать их
ГЛАВА 6 Очереди сообщений System V
ГЛАВА 6 Очереди сообщений System V 6.1. Введениеы Каждой очереди сообщений System V сопоставляется свой идентификатор очереди сообщений. Любой процесс с соответствующими привилегиями (раздел 3.5) может поместить сообщение в очередь, и любой процесс с другими соответствующими
9.
 2. Стеки и очереди
2. Стеки и очереди9.2. Стеки и очереди Стеки и очереди — это первые из встретившихся нам структур, которые, строго говоря, не встроены в Ruby. Иными словами, в Ruby нет классов Stack и Queue, в отличие от Array и Hash (впрочем, класс Queue есть в библиотеке thread.rb, которую мы еще будем рассматривать).И все же в
Связные списки
Связные списки В связных списках последовательный поиск выполняется точно так же, как и в массивах. Тем не менее, элементы проходятся не по индексу, а по указателю Next. Для класса TtdSingleLinkList, описанного в главе 3, можно разработать две следующих функции: первая — для
Связные списки
Связные списки Изучая код листинга 4.9, можно придти к выводу, что маловероятно, чтобы бинарный поиск использовался для связных списков, если, конечно, не воспользоваться индексным доступом к элементам списка, который, как уже упоминалось в главе 3, приводит к снижению
Глава 9.
 Очереди по приоритету и пирамидальная сортировка.
Очереди по приоритету и пирамидальная сортировка.Глава 9. Очереди по приоритету и пирамидальная сортировка. В главе 3 мы рассмотрели несколько очень простых структур данных. Одной из них была очередь. В эту структуру можно было добавлять элементы, а затем извлекать их в порядке поступления. При этом сохранение даты и
Глава 24. Списки команд
Глава 24. Списки команд Средством обработки последовательности из нескольких команд служат списки: «И-списки» и «ИЛИ-списки». Они эффективно могут заменить сложную последовательность вложенных if/then или даже case.Объединение команд в цепочкиИ-списокcommand-1 && command-2 &&
Глава 3 Списки, операторы, арифметика
Глава 3
Списки, операторы, арифметика
В этой главе мы будем изучать специальные способы представления списков. Список — один из самых простых и полезных типов структур. Мы рассмотрим также некоторые программы для выполнения типовых операций над списками и, кроме того,
Список — один из самых простых и полезных типов структур. Мы рассмотрим также некоторые программы для выполнения типовых операций над списками и, кроме того,
У6.9 Ограниченные стеки
У6.9 Ограниченные стеки Измените приведенную в этой лекции спецификацию стеков так, чтобы она описывала стеки ограниченной емкости. (Указание: введите емкость как явную функцию-запрос и сделайте функцию put
У15.5 Связанные стеки
У15.5 Связанные стеки Основываясь на классах STACK и LINKED_LIST, постройте класс LINKED_STACK, описывающий реализацию стека как связного
Типы связанных списков в структурах данных
Связанный список подобен поезду, в котором каждая тележка соединена звеньями. Для облегчения жизни существуют различные типы связанных списков, например средство просмотра изображений, музыкальный проигрыватель или перемещение по веб-страницам.
Существует четыре основных типа связанных списков:
- Односвязные списки
- Двусвязные списки
- Круговые связанные списки
- Циклические двусвязные списки
Односвязный список — это однонаправленный связанный список. Таким образом, вы можете пройти его только в одном направлении, то есть от головного узла к хвостовому узлу.
Структура односвязного списка
Существует множество приложений для односвязных списков. Одним из распространенных приложений является хранение списка элементов, которые необходимо обрабатывать по порядку. Например, односвязный список можно использовать для хранения списка задач, которые необходимо выполнить, при этом головной узел представляет первую задачу, которую необходимо выполнить, а хвостовой узел представляет последнюю задачу, которую необходимо выполнить.
Односвязные списки также часто используются в алгоритмах, которым необходимо обрабатывать список элементов в обратном порядке. Например, популярный алгоритм быстрой сортировки использует односвязный список для хранения списка элементов, которые необходимо отсортировать. Обрабатывая список в обратном порядке, быстрая сортировка может более эффективно сортировать список.
Например, популярный алгоритм быстрой сортировки использует односвязный список для хранения списка элементов, которые необходимо отсортировать. Обрабатывая список в обратном порядке, быстрая сортировка может более эффективно сортировать список.
Создание и обход односвязного списка
Связный список — это структура данных, в которой хранится последовательность элементов. Каждый элемент в списке называется узлом, и каждый узел имеет ссылку на следующий узел в списке. Первый узел в списке называется головным, а последний узел в списке — хвостовым.
Чтобы создать односвязный список, нам сначала нужно создать класс узлов. Каждый узел будет иметь два члена данных: целочисленное значение и ссылку на следующий узел в списке. Далее нам нужно создать класс LinkedList. Этот класс будет иметь два члена данных: головной узел и хвостовой узел. Головной узел будет хранить первый элемент в списке, а хвостовой узел будет хранить последний элемент в списке.
Чтобы добавить элемент в список, нам нужно создать новый узел и установить следующую ссылку предыдущего хвостового узла, чтобы она указывала на новый узел. Затем мы можем установить новый узел в качестве нового хвоста списка.
Затем мы можем установить новый узел в качестве нового хвоста списка.
Чтобы удалить элемент из списка, нам нужно найти узел, содержащий значение, которое мы хотим удалить. Мы можем сделать это, обходя список, пока не найдем узел с совпадающим значением. Как только мы найдем узел, нам нужно установить следующую ссылку предыдущего узла, чтобы она указывала на следующий узел. Чтобы найти элемент в списке, нам нужно пройти по списку, пока мы не найдем узел с совпадающим значением. Чтобы пройти по списку, мы можем начать с головного узла и следовать следующим ссылкам, пока не достигнем хвостового узла.
Двунаправленный связанный список — это двунаправленный связанный список. Таким образом, вы можете пройти его в обоих направлениях. В отличие от односвязных списков, его узлы содержат один дополнительный указатель, называемый предыдущим указателем. Этот указатель указывает на предыдущий узел.
Структура двусвязного списка
Двусвязный список односвязных списков — это структура данных, состоящая из набора односвязных списков (SLL), каждый из которых является двусвязным. Он используется для хранения данных таким образом, чтобы можно было быстро вставлять и удалять элементы.
Он используется для хранения данных таким образом, чтобы можно было быстро вставлять и удалять элементы.
Каждый SLL состоит из двух частей: головы и хвоста. В начале каждого SLL находится указатель на первый элемент в списке, а в конце — указатель на последний элемент.
Преимущество по сравнению с другими структурами данных, поскольку позволяет быстро вставлять и удалять элементы. Кроме того, он прост в реализации и может использоваться в различных приложениях.
Создание и обход двусвязного списка
Двусвязный список — это тип структуры данных, который позволяет хранить данные линейным образом, подобно односвязному списку. Однако, в отличие от односвязного списка, двусвязный список допускает как прямой, так и обратный обход данных, хранящихся в нем. Это делает ее идеальной структурой данных для приложений, которым требуется возможность перемещаться как вперед, так и назад по списку данных.
Чтобы создать двусвязный список, нам сначала нужно создать класс Node, который будет использоваться для хранения наших данных. Этот класс Node будет иметь два атрибута: data и next. Атрибут data будет использоваться для хранения фактических данных, которые мы хотим сохранить в нашем списке, а атрибут next будет использоваться для хранения ссылки на следующий узел в списке.
Этот класс Node будет иметь два атрибута: data и next. Атрибут data будет использоваться для хранения фактических данных, которые мы хотим сохранить в нашем списке, а атрибут next будет использоваться для хранения ссылки на следующий узел в списке.
Когда у нас есть класс Node, мы можем создать двусвязный список. Для этого нам нужно создать класс, который будет представлять наш список. У этого класса будет два атрибута: голова и хвост. Атрибут head будет использоваться для хранения ссылки на первый узел в нашем списке, а атрибут tail будет использоваться для хранения ссылки на последний узел в нашем списке.
После создания класса списка мы можем начать добавлять в него данные. Чтобы добавить данные в наш список, нам нужно создать новый узел и установить для его атрибута данных данные, которые мы хотим добавить. Затем нам нужно установить следующий атрибут нового узла, чтобы он указывал на головной узел нашего списка. Наконец, нам нужно установить головной узел нашего списка так, чтобы он указывал на новый узел.
Теперь, когда мы знаем, как добавлять данные в наш список, мы можем написать функцию для обхода нашего списка. Для этого нам нужно создать переменную, которая будет отслеживать текущий узел, который мы проходим. Мы можем установить эту переменную в головной узел нашего списка, чтобы начать. Затем нам нужно создать цикл while, который будет продолжаться до тех пор, пока текущий узел не станет None, что указывает на то, что мы достигли конца нашего списка.
В нашем цикле while нам нужно распечатать данные, хранящиеся в текущем узле. Затем нам нужно установить текущий узел на следующий узел в нашем списке, прежде чем перейти к следующей итерации цикла.
Круговой связанный список — это однонаправленный связанный список. Таким образом, вы можете пройти его только в одном направлении. Но у этого типа связанного списка последний узел указывает на головной узел. Поэтому во время обхода вам нужно быть осторожным и прекращать обход при повторном посещении головного узла.
Структура кругового связанного списка
Циклический связанный список — это тип структуры данных, в которой используется технология связанных списков для хранения данных линейным последовательным образом. Однако, в отличие от традиционного связанного списка, круговой связанный список не имеет ни начала, ни конца — по сути, это кольцо узлов. Это делает круговые связанные списки идеальными для приложений, в которых данные должны обрабатываться в непрерывном цикле, например, в приложениях реального времени или симуляциях.
Циклические связанные списки обычно реализуются с использованием структуры данных односвязного списка. Это означает, что каждый узел в списке соединен со следующим узлом через указатель. Затем последний узел в списке снова соединяется с первым узлом, создавая кольцевую структуру.
Доступ к данным в циклическом связанном списке аналогичен доступу к данным в традиционном связанном списке. Однако из-за того, что в списке нет определенного начала или конца, может быть трудно понять, с чего начать просмотр списка. В результате во многих реализациях круговых связанных списков используется «головной» указатель, указывающий на первый узел в списке.
В результате во многих реализациях круговых связанных списков используется «головной» указатель, указывающий на первый узел в списке.
Циклические связанные списки имеют ряд преимуществ по сравнению с традиционными связанными списками. Во-первых, поскольку у списка нет определенного начала или конца, данные можно добавлять и удалять из списка в любое время. Это делает круговые связанные списки идеальными для приложений, в которых данные необходимо постоянно добавлять или удалять, например, в приложениях реального времени.
Во-вторых, поскольку данные хранятся в кольцевой структуре, к ним можно обращаться в непрерывном цикле. Это делает круговые связанные списки идеальными для приложений, в которых данные должны обрабатываться в непрерывном цикле, например, в приложении реального времени или моделировании.
В-третьих, поскольку у списка нет определенного начала или конца, круговые связанные списки обычно более эффективны, чем традиционные связанные списки, когда речь идет об использовании памяти. Это связано с тем, что традиционные связанные списки часто требуют дополнительной памяти для указателей, указывающих на начало и конец списка. Циклические связанные списки, с другой стороны, требуют только одного указателя для хранения в памяти — указателя на начало.
Это связано с тем, что традиционные связанные списки часто требуют дополнительной памяти для указателей, указывающих на начало и конец списка. Циклические связанные списки, с другой стороны, требуют только одного указателя для хранения в памяти — указателя на начало.
Наконец, круговые связанные списки часто легче реализовать, чем традиционные связанные списки. Это связано с тем, что традиционные связанные списки часто требуют использования дополнительных структур данных, таких как стеки и очереди, для отслеживания начала и конца списка. Циклические связанные списки, с другой стороны, требуют только структуры данных односвязного списка.
Создание и обход кругового связанного списка
Циклический связанный список — это тип структуры данных, в которой может храниться набор элементов. Это относится как к односвязному списку, так и к двусвязному списку. В отличие от односвязного списка, который имеет указатель NULL в конце списка, круговой связанный список имеет указатель, указывающий на первый узел в списке. Это позволяет просматривать весь список без необходимости отслеживать конец списка.
Это позволяет просматривать весь список без необходимости отслеживать конец списка.
Существует два типа циклических связанных списков: односвязные и двусвязные. В односвязном круговом связанном списке каждый узел имеет указатель, указывающий на следующий узел в списке. Последний узел в списке указывает на первый узел. В двусвязном круговом связанном списке каждый узел имеет указатели, которые указывают как на следующий узел, так и на предыдущий узел.
Круговые связанные списки имеют множество применений. Их можно использовать для реализации очередей, стеков или деков. Их также можно использовать для приложений, которым требуются кольцевые буферы или кольцевые массивы.
Существует два способа создания кругового связанного списка:
- Создайте односвязный список и сделайте так, чтобы последний узел указывал на первый узел.
- Создайте двусвязный список и сделайте так, чтобы последний узел указывал на первый узел, а первый узел указывал на последний узел.

Чтобы создать односвязный циклический связанный список, нам сначала нужно создать односвязный список. Мы можем сделать это, создав класс Node и класс LinkedList. Класс Node будет представлять каждый узел в списке, а класс LinkedList будет представлять сам список.
Чтобы создать двусвязный круговой связанный список, нам сначала нужно создать двусвязный список. Мы можем сделать это, создав класс Node и класс LinkedList. Класс Node будет представлять каждый узел в списке, а класс LinkedList будет представлять сам список.
Создав классы Node и LinkedList, мы можем создать круговой связанный список, создав несколько узлов и связав их вместе. Для этого нам сначала нужно создать несколько узлов. Затем нам нужно связать узлы вместе, чтобы сформировать круговой связанный список. Мы также можем связать узлы вместе в двусвязном списке.
Существует два способа обхода кругового связанного списка:
- Перемещайтесь по списку, пока снова не достигнете головного узла.

- Следите за узлами, которые вы посетили.
Чтобы просмотреть список, пока вы снова не достигнете головного узла, вы можете использовать цикл while. Если вы хотите отслеживать узлы, которые вы посетили, вы можете использовать список или набор.
Круговой двусвязный список представляет собой смесь двусвязного списка и циклического связанного списка. Как и двусвязный список, он имеет дополнительный указатель, называемый предыдущим указателем, и, как и циклический связанный список, его последний узел указывает на головной узел. Этот тип связанного списка является двунаправленным списком. Таким образом, вы можете пройти его в обоих направлениях.
Структура дважды циклически связанного списка
Дважды циклический связанный список (DCL) — это разновидность стандартного двусвязного списка. В DCL первый и последний узлы связаны вместе, образуя круг. Это позволяет быстро и легко перемещаться по всему списку без необходимости специальной обработки регистра в начале или в конце списка. DCL часто используются в приложениях, где данные должны обрабатываться последовательно, например, в видео- или аудиоплеере. Циклический характер списка позволяет быстро и легко перемещаться от одного узла к другому без необходимости обработки особых случаев. DCL также иногда используются в приложениях, где к данным требуется произвольный доступ, например, в базе данных. В этом случае круговой характер списка позволяет быстро и легко перемещаться к любому узлу в списке без необходимости обработки особых случаев.
DCL часто используются в приложениях, где данные должны обрабатываться последовательно, например, в видео- или аудиоплеере. Циклический характер списка позволяет быстро и легко перемещаться от одного узла к другому без необходимости обработки особых случаев. DCL также иногда используются в приложениях, где к данным требуется произвольный доступ, например, в базе данных. В этом случае круговой характер списка позволяет быстро и легко перемещаться к любому узлу в списке без необходимости обработки особых случаев.
Создание и обход дважды кругового связанного списка
Чтобы создать дважды круговой связанный список, нам сначала нужно создать структуру узлов, которая будет содержать наши данные и указатели. Затем мы можем создать указатель на голову и инициализировать его значением null. Далее нам нужно создать функцию для вставки новых узлов в список. Эта функция должна принимать в качестве входных данных данные, которые мы хотим вставить, и указатель на заголовок. Затем он должен создать новый узел с этими данными и вставить его в список. Наконец, нам нужно написать функцию для обхода списка и вывода данных, содержащихся в каждом узле. Эта функция должна принимать в качестве входных данных указатель головы. Затем он должен перебирать каждый узел в списке, распечатывая данные, содержащиеся в этом узле.
Наконец, нам нужно написать функцию для обхода списка и вывода данных, содержащихся в каждом узле. Эта функция должна принимать в качестве входных данных указатель головы. Затем он должен перебирать каждый узел в списке, распечатывая данные, содержащиеся в этом узле.
Далее вы познакомитесь с некоторыми приложениями этих связанных списков.
- Связанный список используется для реализации стека и очередей
- Связный список используется для представления разреженных матриц
- Вы можете реализовать средство просмотра изображений, используя круговой связанный список
- Вы можете использовать концепцию связанного списка для навигации по веб-страницам
- Вы можете использовать круговой двусвязный список для реализации кучи Фибоначчи
Если вы хотите получить навыки, необходимые для работы в сложной, полезной и динамичной роли в сфере ИТ, мы вас поддержим! Откройте для себя бесконечные возможности с помощью этой инновационной программы для аспирантов по курсу Full Stack Web Development, разработанному нашими партнерами из Caltech CTME.Зарегистрируйтесь сегодня!
Следующие шаги
Погружение в особенности «Односвязных списков» может стать вашей следующей остановкой. Связанные списки состоят из узлов, которые указывают на следующий узел. Связанные списки являются динамическими и имеют более быстрое время вставки/удаления.
Ищете онлайн-обучение и сертификацию в области разработки программного обеспечения? Simplilearn предлагает множество программ, в том числе программу для аспирантов по веб-разработке полного стека в сотрудничестве с Caltech CTME.
Если у вас есть какие-либо вопросы об этом руководстве, пожалуйста, не стесняйтесь оставлять их в разделе комментариев ниже. Наша круглосуточная команда экспертов обязательно ответит на все ваши вопросы как можно скорее.
Как реализовать связанный список в JavaScript
Если вы изучаете структуры данных, вам следует знать связанный список. Если вы не совсем понимаете, как это реализовано в JavaScript, эта статья поможет вам.
В этой статье мы обсудим, что такое связанный список, чем он отличается от массива и как его реализовать в JavaScript. Давайте начнем.
Связный список — это линейная структура данных, похожая на массив. Однако, в отличие от массивов, элементы не хранятся в определенной ячейке памяти или индексе. Скорее каждый элемент представляет собой отдельный объект, который содержит указатель или ссылку на следующий объект в этом списке.
Каждый элемент (обычно называемый узлами) содержит два элемента: сохраненные данные и ссылку на следующий узел. Данные могут быть любого допустимого типа данных. Вы можете увидеть это на диаграмме ниже.
Точка входа в связанный список называется головой. Голова — это ссылка на первый узел в связанном списке. Последний узел в списке указывает на ноль. Если список пуст, заголовок является нулевой ссылкой.
В JavaScript связанный список выглядит так:
const list = {
глава: {
значение: 6
следующий: {
значение: 10
следующий: {
значение: 12
следующий: {
значение: 3
следующий: ноль
}
}
}
}
}
}; РЕКЛАМА
- Узлы можно легко удалять или добавлять из связанного списка без реорганизации всей структуры данных.
 Это одно из его преимуществ перед массивами.
Это одно из его преимуществ перед массивами.
- Операции поиска в связанных списках выполняются медленно. В отличие от массивов, произвольный доступ к элементам данных не допускается. Доступ к узлам осуществляется последовательно, начиная с первого узла.
- Использует больше памяти, чем массивы, из-за хранения указателей.
Существует три типа связанных списков:
- Односвязные списки : Каждый узел содержит только один указатель на следующий узел. Это то, о чем мы говорили до сих пор.
- Двусвязные списки : Каждый узел содержит два указателя, указатель на следующий узел и указатель на предыдущий узел.
- Циклические связанные списки : Циклические связанные списки представляют собой вариант связанного списка, в котором последний узел указывает на первый узел или любой другой узел перед ним, тем самым образуя петлю.
РЕКЛАМА
Реализация узла списка в JavaScript
Как было сказано ранее, узел списка содержит два элемента: данные и указатель на следующий узел. Мы можем реализовать узел списка в JavaScript следующим образом:
Мы можем реализовать узел списка в JavaScript следующим образом:
class ListNode {
конструктор (данные) {
это.данные = данные
это.следующее = ноль
}
} В приведенном ниже коде показана реализация класса связанного списка с конструктором. Обратите внимание, что если головной узел не передается, он инициализируется нулем.
класс LinkedList {
конструктор (голова = ноль) {
это.голова = голова
}
} Собираем все вместе
Давайте создадим связанный список с только что созданным классом. Сначала мы создаем два узла списка, node1 и node2 , а также указатель с узла 1 на узел 2.
let node1 = new ListNode(2) пусть node2 = новый ListNode (5) node1.next = node2
Далее мы создадим связанный список с node1 .
пусть список = новый LinkedList (узел 1)
Давайте попробуем получить доступ к узлам в списке, который мы только что создали.
console.log(list.head.next.data) // возвращает 5
РЕКЛАМА
Далее мы реализуем четыре вспомогательных метода для связанного списка. Вот они:
- size()
- clear()
- getLast()
- getFirst()
1. size()
Этот метод возвращает количество узлов, присутствующих в связанном списке.
размер() {
пусть счет = 0;
пусть узел = this.head;
в то время как (узел) {
количество++;
узел = узел.следующий
}
количество возвратов;
}
2. clear()
Этот метод очищает список.
очистить () {
this.head = ноль;
} РЕКЛАМА
3. getLast()
Этот метод возвращает последний узел связанного списка.
получитьПоследнее() {
пусть lastNode = this.head;
если (последний узел) {
в то время как (последний узел. следующий) {
последнийУзел = последнийУзел.следующий
}
}
вернуть последний узел
} 4.
 getFirst()
getFirst()Этот метод возвращает первый узел связанного списка.
получитьПервый() {
вернуть this.head;
} Резюме
В этой статье мы обсудили, что такое связанный список и как его можно реализовать в JavaScript. Мы также обсудили различные типы связанных списков, а также их общие преимущества и недостатки.
Надеюсь, вам понравилось читать.
Хотите получать уведомления, когда я публикую новую статью? Кликните сюда.
Научитесь программировать бесплатно. Учебная программа freeCodeCamp с открытым исходным кодом помогла более чем 40 000 человек получить работу в качестве разработчиков. Начать
РЕКЛАМА
С#. Каковы реальные примеры использования связанных списков?
спросил
Изменено 13 дней назад
Просмотрено 25 тысяч раз
Другой программист упомянул, что за всю его карьеру они не нашли варианта использования структуры данных связанного списка ни в одном профессиональном программном обеспечении. Я не мог придумать ни одного хорошего примера из головы. Он в основном разработчик C# и Java
Я не мог придумать ни одного хорошего примера из головы. Он в основном разработчик C# и Java
Может ли кто-нибудь привести несколько примеров, когда это была правильная структура данных для решения конкретной реальной проблемы?
Связанный: Каков практический, реальный пример связанного списка?
Связанный список структур данных Java в С#
1
Связанные списки имеют ряд преимуществ по сравнению с сопоставимыми структурами данных, такими как статические или динамически расширяемые массивы.
- LinkedLists не требует непрерывных блоков памяти, поэтому может помочь уменьшить фрагментацию памяти
- LinkedLists поддерживают эффективное удаление элементов (динамические массивы обычно вызывают сдвиг всех элементов).
- LinkedLists поддерживают эффективное добавление элементов (динамические массивы могут вызвать перераспределение + копирование, если конкретное добавление превышает текущую емкость)
Любое место, где эти преимущества были бы очень ценны для программы (а недостатки LinkedList были незначительными), можно было бы использовать LinkedList.
9
Реальным примером может быть очередь FIFO. Простой список на основе массива довольно плох для этого, потому что вам нужно добавить на одном конце и удалить на другом конце, и одна из этих операций будет O (n) со списком на основе массива (если вы не добавите дополнительную логику к работать с начальным И конечным индексом), в то время как оба являются O (1) со связанным списком без дополнительных усилий.
5
Назойливые связанные списки — интересные звери для разработки игр. Например, довольно распространенной практикой является наличие назойливого одно- или двусвязного списка «рендеринга»:
класс Renderable /* или класс Object, что угодно */
{
// ...
Рендеринг * m_pNext;
Рендеринг * m_pPrev; // или нет, если односвязный
// ...
}
Когда Renderables появляются и исчезают, они могут регистрироваться в этом списке, не вызывая выделения памяти. Если их глубина рендеринга или приоритет изменены, они могут удалить и снова вставить себя и т. д.
Если их глубина рендеринга или приоритет изменены, они могут удалить и снова вставить себя и т. д.
Когда придет время рендеринга, все, что вам нужно сделать, это найти начало списка и прокрутить его, вызвав соответствующий метод!
(Есть, конечно, много вариаций на эту тему, с несколькими отдельными списками и т. д. И вам не нужно иметь навязчивый список, чтобы это работало, я просто нахожу навязчивые интересные.)
1
Связанные списки (в паре с хеш-таблицей) действительно полезны для кэшей LRU.
Каждому Get необходимо поместить узел в начало списка, что очень дешево для связанных списков.
Пример односвязного списка.
- Кнопка отмены любого приложения, такого как Microsoft Word, Paint и т. д.: связанный список состояний.
- GPS-навигация: связанный список картографических данных. Путешествие от источника к месту назначения является примером обхода всех узлов.
 Перенаправление
с помощью GPS является примером операций добавления и удаления картографических данных.
Перенаправление
с помощью GPS является примером операций добавления и удаления картографических данных.
Пример двусвязного списка.
- Кнопки браузера «Далее» и «Назад»: связанный список URL-адресов.
- Кнопки «Далее» и «Назад» средства просмотра изображений: связанный список изображений
- Кнопка «Отменить» и «Повторить» в Photoshop, связанный список состояний.
Стеки и очереди — очень наглядные примеры связанных списков, но, поскольку другие уже упоминали о них, я хотел бы добавить еще несколько примеров:
DOM хранит узлы в виде связанных списков. Простой пример javascript, который действительно одинаков на любом языке:
for (var node = parent.firstChild; node != null; node = node.nextSibling) {
// ..
}
Я полагаю, что разработчик Java в какой-то момент столкнулся с XML.
Деревья — еще один хороший пример связанных списков, хотя они и не являются простыми одномерными списками. Кто-то, кто занимался разработкой Java, вероятно, сталкивался с TreeMaps и TreeSets.
Кто-то, кто занимался разработкой Java, вероятно, сталкивался с TreeMaps и TreeSets.
Все обсуждение кажется мне немного глупым. Связанные списки — это фундаментальная структура данных, которая используется повсеместно. Единственная причина, по которой кто-то может подумать, что он или она не сталкивался с ними, заключается в том, что вам не нужно беспокоиться о реализации структур данных в современных языках высокого уровня, но, конечно, они все еще там.
Они возникают постоянно, везде, где объект имеет свойство, указывающее на другой объект того же типа. В среде CLR исключения образуют связанный список из-за свойства InnerException .
Неизменяемый связанный список является очень ценной структурой, так как вы можете «делить структуру» с другими списками с тем же хвостом. Большинство функциональных языков включают тип неизменяемого связанного списка в качестве одной из своих основных структур данных, и эти типы используются повсеместно.
1
Я написал расширение BIOS (по сути, драйвер устройства для BIOS, написанный на ассемблере) для хост-контроллера USB. — Реализация высокоуровневой, казалось бы, абстрактной структуры данных, такой как связанный список в ассемблере, не так сложна, как кажется. — Контроллер обслуживал запросы ввода-вывода для клавиатуры и диска, используя связанный список пакетов в основной памяти. Я поддерживал пул бесплатных пакетов в другом связанном списке. Выполнение ввода-вывода в основном включало захват свободного пакета из начала списка свободных, настройку пакета, добавление пакета в список устройств и повторное добавление пакета в начало свободного пула после завершения ввода-вывода. Связанные списки позволяют молниеносно перемещаться по таким объектам, особенно когда объекты большие, поскольку на самом деле им не нужно двигаться. Только их указатели должны быть обновлены.
— Реализация высокоуровневой, казалось бы, абстрактной структуры данных, такой как связанный список в ассемблере, не так сложна, как кажется. — Контроллер обслуживал запросы ввода-вывода для клавиатуры и диска, используя связанный список пакетов в основной памяти. Я поддерживал пул бесплатных пакетов в другом связанном списке. Выполнение ввода-вывода в основном включало захват свободного пакета из начала списка свободных, настройку пакета, добавление пакета в список устройств и повторное добавление пакета в начало свободного пула после завершения ввода-вывода. Связанные списки позволяют молниеносно перемещаться по таким объектам, особенно когда объекты большие, поскольку на самом деле им не нужно двигаться. Только их указатели должны быть обновлены.
Очередь на основе массива потребовала бы:
- с использованием указателя индекса начала/конца, который работает быстро, но требует фиксирования размера очереди, чтобы производителю приходилось ждать, когда очередь потребителя заполнится, и блокировать очередь при этом заполняется весь пакет, если производителей более одного
- сдвигает все элементы в очереди всякий раз, когда вы вставляете/удаляете их, что замедляет работу с большими объектами
Таким образом, связанные списки — хороший способ реализовать произвольно длинную очередь больших объектов в порядке поступления.
Еще одна вещь, о которой следует быть осторожным, это то, что для небольших объектов или когда вы размещаете объекты из обычной кучи вместо пользовательского свободного пула, массивы могут быть быстрее, потому что копирование на самом деле не такое уж медленное, если оно не выполняется так часто, и повторное выделение из кучи, которое потребовалось бы для связанного списка каждый раз, когда добавляется новый элемент, происходит медленно.
Конечно, вы можете захотеть смоделировать и измерить конкретный сценарий с помощью одноразового тестового кода, чтобы найти ответ. Мне нравится запускать циклы несколько миллионов раз со связанными списками и массивами, с маленькими и большими объектами, и измерять, сколько времени занимает каждый из них в реальном времени. Иногда вы будете удивлены.
В качестве, возможно, лучшего реального примера в .Net рассмотрим MultiCastDelegate.
Связанные списки, реализованные таким образом, где аспект цепочки списков поддерживается непосредственно в типе, а не в отдельном контейнере, могут быть чрезвычайно мощными и эффективными. Однако они приходят с различными компромиссами.
Однако они приходят с различными компромиссами.
Одним из очевидных является дублирование кода, вы должны запечь эту логику в каждом типе. Такие методы, как расширение базового класса, предоставляющего указатель, запутаны (вы теряете строгую типизацию без обобщений) и часто неприемлемы с точки зрения производительности.
Другое дело, что вы ограничены одной реализацией каждого типа. Вы не можете превратить односвязную структуру в двусвязную без вставки дополнительного поля в каждый экземпляр и обновления всего соответствующего кода.
Как уже было сказано, уже связанные списки очень полезны, когда вам нужно вставлять и удалять элементы.
Например, чтобы облегчить отладку управления памятью в моем коде, я недавно реализовал список ссылок между всеми моими объектами с подсчетом ссылок, чтобы в конце программы (когда все ссылки должны были достичь нуля и удалить объекты) я мог точно видеть то, что еще оставалось, что обычно приводило к тому, что я мог найти единственный объект в корне проблемы.
CPython реализует что-то похожее с массивным связанным списком почти каждый раз, когда он построен с отладкой.
Отвечая тегу «Структуры данных», на низком уровне, таком как сборка, связанные списки являются идеальным способом хранения списков переменной длины других структур данных. Нет дополнительных затрат на поддержание длины или конца списка, и нет необходимости в элементах списка фиксированного размера. Последняя причина также относится к языкам более высокого уровня.
Связный список — это основная структура данных для Dancing Links, метода, используемого для эффективной реализации алгоритма X, который представляет собой алгоритм поиска с возвратом для поиска всех решений NP-полной задачи точного покрытия, к которой естественным образом сводятся многие сложные задачи. к.
Стеки и очереди являются примерами связанных списков.
2
Как указывает daustin777, связанные списки окружают вас повсюду, и вы можете даже не подозревать об этом. Но практичность вопроса в том, что они позволяют выполнять некоторые довольно простые операции с относительной легкостью и гибкостью. Например, не сортировать, а просто поменять местами указатели. Нужно вставить или удалить в произвольных местах? Вставьте или удалите указатели в списке. Нужно перебирать вперед и назад… связанный список. Хотя это и не совсем бизнес-пример, я надеюсь, что это достаточно проясняет его для вас, чтобы применить его к вашему реальному бизнес-кейсу.
Но практичность вопроса в том, что они позволяют выполнять некоторые довольно простые операции с относительной легкостью и гибкостью. Например, не сортировать, а просто поменять местами указатели. Нужно вставить или удалить в произвольных местах? Вставьте или удалите указатели в списке. Нужно перебирать вперед и назад… связанный список. Хотя это и не совсем бизнес-пример, я надеюсь, что это достаточно проясняет его для вас, чтобы применить его к вашему реальному бизнес-кейсу.
Если я могу ответить на этот вопрос немного иначе, чем другие, то в последнее время я использую связанные списки для организации музыкальных списков. Списки обеспечивают отличный способ хранения и сортировки музыки по исполнителю, песне, альбому, даже по рейтингу или продолжительности песни. У меня двусвязный список, но я вижу, что он применим и к односвязному списку. Списки покупок тоже подойдут, а если у вас ОКР, как у моей мамы, вы можете легко организовать его между рядами и замороженными продуктами в последнюю очередь!
Если мы включим стеки и очереди, очевидным для очередей будет очередь печати или музыкальный плейлист (списки в любом смысле, очевидно, хороши).
Для задач, где максимальное количество узлов ограничено 100 или меньше или около того, разумным решением являются связанные списки. То же самое можно сказать и о таких вещах, как пузырьковая сортировка и других вещах, которые считаются неоптимальными.
Реализация связанного списка обнаружена в дикой природе:
Кэш Python LRU:
...
...
cache_get = cache.get # связанный метод для поиска ключа или возврата None
cache_len = cache.__len__ # получить размер кеша без вызова len()
lock = RLock() # потому что обновления связанного списка не являются потокобезопасными
root = [] # корень кругового двусвязного списка
...
...
Однако обратите внимание, что функция _lru_cache_wrapper на самом деле импортирована из реализации C-модуля :
...
...
структура typedef lru_list_elem {
PyObject_HEAD
структура lru_list_elem *пред., *след.; /* заимствованные ссылки */
хэш Py_hash_t;
PyObject *ключ, *результат;
} lru_list_elem;
. ..
...
..
...
Плюсы связанного списка:
- Динамическое хранилище сводит на нет фрагментацию
- Быстрая установка/удаление
- Быстрый доступ к первому элементу (и конец, если реализован двунаправленный)
- Эффективное использование памяти
Минусы связанного списка:
- Медленное перемещение
Внезапно я бы реализовал стеки, очереди и насосы сообщений, используя связанные списки. Я бы также реализовал дерево данных, используя связанные списки с несколькими ссылками для быстрой вставки/удаления.
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Введение — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Работа со связанными списками в Python
Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Работа со связанными списками в Python
Связанные списки похожи на менее известный родственник списков. Они не так популярны и не так круты, и вы можете даже не помнить их из своего класса алгоритмов. Но в правильном контексте они действительно могут блистать.
В этой статье вы узнаете:
- Что такое связанные списки и когда их следует использовать
- Как использовать
collections.dequeдля всех потребностей вашего связанного списка - Как реализовать собственные связанные списки
- Какие существуют другие типы связанных списков и для чего их можно использовать
Если вы хотите освежить свои навыки программирования для собеседования или если вы хотите узнать больше о структурах данных Python помимо обычных словарей и списков, то вы попали в нужное место!
Вы можете следовать примерам из этого руководства, загрузив исходный код, доступный по ссылке ниже:
Общие сведения о связанных списках
Связанные списки — это упорядоченный набор объектов. Так чем же они отличаются от обычных списков? Связанные списки отличаются от списков способом хранения элементов в памяти. В то время как списки используют непрерывный блок памяти для хранения ссылок на свои данные, связанные списки хранят ссылки как часть своих собственных элементов.
Так чем же они отличаются от обычных списков? Связанные списки отличаются от списков способом хранения элементов в памяти. В то время как списки используют непрерывный блок памяти для хранения ссылок на свои данные, связанные списки хранят ссылки как часть своих собственных элементов.
Удалить рекламу
Основные понятия
Прежде чем углубляться в то, что такое связанные списки и как вы можете их использовать, вы должны сначала узнать, как они структурированы. Каждый элемент связанного списка называется узлом , и каждый узел имеет два разных поля:
.- Данные содержат значение, которое должно быть сохранено в узле.
- Next содержит ссылку на следующий узел в списке.
Вот как выглядит типичный узел:
Узел Связный список — это набор узлов. Первый узел называется head и используется в качестве отправной точки для любой итерации по списку. Последний узел должен иметь ссылку
Последний узел должен иметь ссылку next , указывающую на None , чтобы определить конец списка. Вот как это выглядит:
Теперь, когда вы знаете, как устроен связанный список, вы готовы рассмотреть некоторые практические варианты его использования.
Практическое применение
Связанные списки служат различным целям в реальном мире. Их можно использовать для реализации ( предупреждение о спойлере! ) очередей или стеков, а также графов. Они также полезны для гораздо более сложных задач, таких как управление жизненным циклом приложения операционной системы.
Очереди или стеки
Очереди и стеки различаются только способом извлечения элементов. Для очереди используется подход First In/First Out (FIFO). Это означает, что первый элемент, вставленный в список, будет извлечен первым:
Очередь На диаграмме выше вы можете увидеть передних и задних элементов очереди. Когда вы добавляете новые элементы в очередь, они переходят в конец очереди. Когда вы извлекаете элементы, они берутся из начала очереди.
Когда вы добавляете новые элементы в очередь, они переходят в конец очереди. Когда вы извлекаете элементы, они берутся из начала очереди.
Для стека используется подход Last-In/Fist-Out (LIFO), означающий, что последний элемент, вставленный в список, извлекается первым:
Stack На приведенной выше диаграмме видно, что первый элемент, вставленный в стек (индекс 0 ) находится внизу, а последний вставленный элемент — вверху. Поскольку в стеках используется подход LIFO, последний вставленный элемент (сверху) будет извлечен первым.
Из-за способа вставки и извлечения элементов из краев очередей и стеков связанные списки являются одним из наиболее удобных способов реализации этих структур данных. Вы увидите примеры этих реализаций позже в статье.
Графики
Графики можно использовать для отображения взаимосвязей между объектами или для представления различных типов сетей. Например, визуальное представление графа — скажем, ориентированного ациклического графа (DAG) — может выглядеть так:
Направленный ациклический граф Существуют разные способы реализации графов, подобных приведенным выше, но один из наиболее распространенных — использование списка смежности . Список смежности — это, по сути, список связанных списков, в котором каждая вершина графа хранится вместе с набором связанных вершин:
Список смежности — это, по сути, список связанных списков, в котором каждая вершина графа хранится вместе с набором связанных вершин:
| Вершина | Связанный список вершин |
|---|---|
| 1 | 2 → 3 → Нет |
| 2 | 4 → Нет |
| 3 | Нет |
| 4 | 5 → 6 → Нет |
| 5 | 6 → Нет |
| 6 | Нет |
В приведенной выше таблице каждая вершина вашего графа указана в левом столбце. Правый столбец содержит ряд связанных списков, в которых хранятся другие вершины, связанные с соответствующей вершиной в левом столбце. Этот список смежности также может быть представлен в коде с помощью дикт :
>>>
>>> график = {
... 1: [2, 3, Нет],
... 2: [4, Нет],
... 3: [Нет],
... 4: [5, 6, Нет],
... 5: [6, Нет],
. .. 6: [Нет]
... }
.. 6: [Нет]
... }
Ключи этого словаря являются исходными вершинами, а значение каждого ключа представляет собой список. Этот список обычно реализуется как связанный список.
Примечание: В приведенном выше примере можно было бы не сохранять значения None , но мы сохранили их здесь для ясности и согласованности с последующими примерами.
С точки зрения скорости и памяти реализация графов с использованием списков смежности очень эффективна по сравнению, например, с матрицей смежности . Вот почему связанные списки так полезны для реализации графа.
Удалить рекламу
Сравнение производительности: списки и связанные списки
В большинстве языков программирования существуют явные различия в способах хранения связанных списков и массивов в памяти. Однако в Python списки представляют собой динамические массивы. Это означает, что использование памяти как для списков, так и для связанных списков очень похоже.
Дополнительная литература: Реализация динамических массивов в Python весьма интересна и определенно заслуживает прочтения. Обязательно посмотрите и используйте эти знания, чтобы выделиться на следующей корпоративной вечеринке!
Поскольку разница в использовании памяти между списками и связанными списками настолько незначительна, лучше сосредоточиться на их различиях в производительности, когда речь идет о временной сложности.
Вставка и удаление элементов
В Python вы можете вставлять элементы в список, используя .insert() или .append() . Для удаления элементов из списка вы можете использовать их аналоги: .remove() и .pop() .
Основное различие между этими методами заключается в том, что вы используете .insert() и .remove() для вставки или удаления элементов в определенной позиции в списке, но вы используете .append() и . только для вставки или удаления элементов в конце списка. pop ()
pop ()
Что вам нужно знать о списках Python, так это то, что вставка или удаление элементов, которые , а не в конце списка, требует смещения некоторого элемента в фоновом режиме, что делает операцию более сложной с точки зрения затрачиваемого времени. Вы можете прочитать упомянутую выше статью о том, как списки реализованы в Python, чтобы лучше понять, как реализация .insert() , .remove() , .append() и .pop() влияет на их производительность.
Имея все это в виду, даже при вставке элементов в конец списка с использованием .append() или .insert() будет иметь постоянное время, O (1), когда вы пытаетесь вставить элемент ближе или в начало списка, средняя временная сложность будет расти вместе с размером списка: О ( n ).
Связанные списки, с другой стороны, намного проще, когда речь идет о вставке и удалении элементов в начале или конце списка, где их временная сложность всегда постоянна: O (1).
По этой причине связанные списки имеют преимущество в производительности по сравнению с обычными списками при реализации очереди (FIFO), в которой элементы непрерывно вставляются и удаляются в начале списка. Но они работают аналогично списку при реализации стека (LIFO), в котором элементы вставляются и удаляются в конце списка.
Извлечение элементов
Когда дело доходит до поиска элементов, списки работают намного лучше, чем связанные списки. Когда вы знаете, к какому элементу хотите получить доступ, списки могут выполнять эту операцию за 9 секунд.0278 О (1) раз. Попытка сделать то же самое со связанным списком потребует O ( n ), потому что вам нужно пройти весь список, чтобы найти элемент.
Однако при поиске определенного элемента как списки, так и связанные списки работают очень одинаково, с временной сложностью O ( n ). В обоих случаях вам нужно перебрать весь список, чтобы найти нужный элемент.
Представляем
collections. deque
deque В Python в модуле collections есть специальный объект, который вы можете использовать для связанных списков, который называется deque (произносится как «колода»), что означает двусторонняя очередь .
collections.deque использует реализацию связанного списка, в котором вы можете получить доступ, вставить или удалить элементы из начала или конца списка с постоянной O (1) производительностью.
Как использовать
collections.deque Существует довольно много методов, которые по умолчанию поставляются с объектом deque . Однако в этой статье вы коснетесь только некоторых из них, в основном для добавления или удаления элементов.
Во-первых, вам нужно создать связанный список. Вы можете использовать следующий фрагмент кода, чтобы сделать это с deque :
>>>
>>> из очереди импорта коллекций >>> очередь() двойная очередь ([])
Приведенный выше код создаст пустой связанный список. Если вы хотите заполнить его при создании, вы можете поставить ему повторяемый в качестве ввода:
Если вы хотите заполнить его при создании, вы можете поставить ему повторяемый в качестве ввода:
>>>
>>> deque(['a','b','c'])
deque(['a', 'b', 'c'])
>>> deque('abc')
deque(['a', 'b', 'c'])
>>> deque([{'данные': 'a'}, {'данные': 'b'}])
deque([{'данные': 'а'}, {'данные': 'б'}])
При инициализации объекта deque в качестве входных данных можно передать любой итерируемый объект, например строку (также итерируемый) или список объектов.
Теперь, когда вы знаете, как создать объект deque , вы можете взаимодействовать с ним, добавляя или удаляя элементы. Вы можете создать abcde связанный список и добавьте новый элемент f следующим образом:
>>>
>>> список = deque("abcde")
>>> список
deque(['a', 'b', 'c', 'd', 'e'])
>>> llist.append("f")
>>> список
deque(['a', 'b', 'c', 'd', 'e', 'f'])
>>> список. поп()
'ф'
>>> список
deque(['a', 'b', 'c', 'd', 'e'])
поп()
'ф'
>>> список
deque(['a', 'b', 'c', 'd', 'e'])
Оба append() и pop() добавляют или удаляют элементы с правой стороны связанного списка. Однако вы также можете использовать deque для быстрого добавления или удаления элементов с левой стороны, или head , из списка:
>>>
>>> llist.appendleft("z")
>>> список
deque(['z', 'a', 'b', 'c', 'd', 'e'])
>>> llist.popleft()
'г'
>>> список
deque(['a', 'b', 'c', 'd', 'e'])
Добавление или удаление элементов с обоих концов списка довольно просто с помощью объекта deque . Теперь вы готовы научиться использовать collections.deque 9.0215 для реализации очереди или стека.
Удаление рекламы
Как реализовать очереди и стеки
Как вы узнали выше, основное различие между очередью и стеком заключается в способе извлечения элементов из каждой очереди. Далее вы узнаете, как использовать
Далее вы узнаете, как использовать collections.deque для реализации обеих структур данных.
Очереди
При использовании очередей вы хотите добавить значения в список ( enqueue ), а когда время подходит, вы хотите удалить элемент, который находился в списке дольше всех ( удален из очереди ). Например, представьте себе очередь в модном и полностью забитом ресторане. Если бы вы пытались внедрить справедливую систему рассадки гостей, вы бы начали с создания очереди и добавления людей по мере их поступления:
>>>
>>> из очереди импорта коллекций
>>> очередь = deque()
>>> очередь
двойная очередь ([])
>>> queue.append("Мария")
>>> queue.append("Джон")
>>> queue.append("Сьюзен")
>>> очередь
deque(['Мэри', 'Джон', 'Сьюзен'])
Теперь у вас в очереди Мэри, Джон и Сьюзан. Помните, что, поскольку очереди FIFO, первый человек, который попал в очередь, должен быть первым, кто выйдет из нее.
Теперь представьте, что проходит некоторое время, и несколько столов становятся доступными. На этом этапе вы хотите удалить людей из очереди в правильном порядке. Вот как вы это сделаете:
>>>
>>> очередь.popleft() 'Мэри' >>> очередь deque(['Джон', 'Сьюзен']) >>> очередь.popleft() 'Джон' >>> очередь deque(['Сьюзен'])
Каждый раз, когда вы вызываете popleft() , вы удаляете элемент head из связанного списка, имитируя реальную очередь.
Стеки
Что если вместо этого вы захотите создать стек? Ну, идея примерно та же, что и с очередью. Единственное отличие состоит в том, что в стеке используется подход LIFO, а это означает, что последний элемент, который будет вставлен в стек, должен быть удален первым.
Представьте, что вы создаете функцию истории веб-браузера, в которой сохраняется каждая страница, которую посещает пользователь, чтобы он мог легко вернуться в прошлое. Предположим, что это действия случайного пользователя в своем браузере:
- Посещение веб-сайта Real Python
- Переход к Pandas: как читать и записывать файлы
- Щелчки по ссылке для чтения и записи файлов CSV в Python
Если вы хотите отобразить это поведение в стек, вы можете сделать что-то вроде этого:
>>>
>>> из очереди импорта коллекций >>> история = deque() >>> history.appendleft("https://realpython.com/") >>> history.appendleft("https://realpython.com/pandas-read-write-files/") >>> history.appendleft("https://realpython.com/python-csv/") >>> история deque(['https://realpython.com/python-csv/', 'https://realpython.com/pandas-read-write-files/', 'https://realpython.com/'])
В этом примере вы создали пустой объект history , и каждый раз, когда пользователь посещал новый сайт, вы добавляли его в переменную history с помощью appendleft() . Это гарантировало, что каждый новый элемент будет добавлен к заголовку связанного списка.
Теперь предположим, что после прочтения обеих статей пользователь захотел вернуться на домашнюю страницу Real Python, чтобы выбрать новую статью для чтения. Зная, что у вас есть стек и вы хотите удалить элементы с помощью LIFO, вы можете сделать следующее:
>>>
>>> history.popleft() 'https://realpython.com/python-csv/' >>> история.popleft() 'https://realpython.com/pandas-read-write-files/' >>> история deque(['https://realpython.com/'])
Ну вот! Используя popleft() , вы удалили элементы из заголовка связанного списка, пока не достигли домашней страницы Real Python.
Из приведенных выше примеров видно, насколько полезно иметь collections.deque в вашем наборе инструментов, поэтому обязательно используйте его в следующий раз, когда вам нужно будет решить задачу на основе очереди или стека.
Удаление рекламы
Реализация собственного связанного списка
Теперь, когда вы знаете, как использовать collections.deque для обработки связанных списков, вам может быть интересно, зачем вам вообще реализовывать свой собственный связанный список в Python. Есть несколько причин сделать это:
- Отработка навыков работы с алгоритмами Python
- Изучение теории структуры данных
- Подготовка к собеседованию
Не стесняйтесь пропустить следующий раздел, если вас не интересует что-либо из вышеперечисленного или если вы уже преуспели в реализации собственного связанного списка в Python. В противном случае пришло время реализовать некоторые связанные списки!
В противном случае пришло время реализовать некоторые связанные списки!
Как создать связанный список
Прежде всего, создайте класс для представления вашего связанного списка:
класс LinkedList:
защита __init__(сам):
self.head = Нет
Единственная информация, которую необходимо хранить для связанного списка, — это начало списка ( глава списка). Затем создайте еще один класс для представления каждого узла связанного списка:
:
def __init__(я, данные):
self.data = данные
self.next = Нет
В приведенном выше определении класса вы можете увидеть два основных элемента каждого отдельного узла: данные и следующий . Вы также можете добавить __repr__ к обоим классам, чтобы иметь более полезное представление объектов:
класс Узел:
def __init__(я, данные):
self.data = данные
self. next = Нет
защита __repr__(сам):
вернуть self.data
класс LinkedList:
защита __init__(сам):
self.head = Нет
защита __repr__(сам):
узел = self.head
узлы = []
в то время как node не None:
узлы.добавлять(узел.данные)
узел = узел.следующий
узлы.append("Нет")
вернуть " -> ".join (узлы)
next = Нет
защита __repr__(сам):
вернуть self.data
класс LinkedList:
защита __init__(сам):
self.head = Нет
защита __repr__(сам):
узел = self.head
узлы = []
в то время как node не None:
узлы.добавлять(узел.данные)
узел = узел.следующий
узлы.append("Нет")
вернуть " -> ".join (узлы)
Взгляните на пример использования вышеуказанных классов для быстрого создания связанного списка с тремя узлами:
>>>
>>> llist = LinkedList()
>>> список
Никто
>>> first_node = узел ("а")
>>> llist.head = первый_узел
>>> список
а -> Нет
>>> второй_узел = узел ("б")
>>> третий_узел = узел ("с")
>>> первый_узел.следующий = второй_узел
>>> второй_узел.следующий = третий_узел
>>> список
а -> б -> в -> нет
Определив значения данных узла и следующих , вы можете довольно быстро создать связанный список. Эти Классы LinkedList и Node являются отправной точкой для нашей реализации. Отныне все дело в увеличении их функциональности.
Отныне все дело в увеличении их функциональности.
Вот небольшое изменение связанного списка __init__() , которое позволяет быстро создавать связанные списки с некоторыми данными:
по определению __init__(я, узлы=Нет):
self.head = Нет
если узлы не None:
узел = узел (данные = узлы.поп (0))
self.head = узел
для элемента в узлах:
node.next = узел (данные = элемент)
узел = узел.следующий
С приведенной выше модификацией создание связанных списков для использования в приведенных ниже примерах станет намного быстрее.
Как просмотреть связанный список
Одна из наиболее частых вещей, которые вы будете делать со связанным списком, — это пересечь его. Обход означает обход каждого отдельного узла, начиная с заголовка связанного списка и заканчивая узлом, который имеет следующее значение None .
Обход — это просто более изящный способ сказать «итерация». Итак, имея это в виду, создайте
Итак, имея это в виду, создайте __iter__ , чтобы добавить к связанным спискам такое же поведение, как и к обычному списку:
по определению __iter__(я):
узел = self.head
в то время как node не None:
узел выхода
узел = узел.следующий
Приведенный выше метод проходит по списку и возвращает все узлы. Самое важное, что нужно помнить об этом __iter__ , это то, что вам нужно всегда проверять, что текущий узел не является None . Когда это условие равно True , это означает, что вы достигли конца своего связанного списка.
После получения текущего узла вы хотите перейти к следующему узлу в списке. Вот почему вы добавляете node = node.next . Вот пример обхода случайного списка и вывода каждого узла:
>>>
>>> llist = LinkedList(["a", "b", "c", "d", "e"]) >>> список a -> b -> c -> d -> e -> нет >>> для узла в списке: ... печать (узел) а б с г е
В других статьях вы могли видеть, что обход определен в конкретном методе с именем traverse() . Однако использование встроенных методов Python для достижения указанного поведения делает эту реализацию связанного списка немного более похожей на Python.
Удалить рекламу
Как вставить новый узел
Существуют разные способы вставки новых узлов в связанный список, каждый со своей реализацией и уровнем сложности. Вот почему вы увидите, что они разделены на определенные методы для вставки в начало, конец или между узлами списка.
Вставка в начале
Вставка нового узла в начало списка, вероятно, является самой простой вставкой, так как вам не нужно проходить весь список, чтобы сделать это. Все дело в создании нового узла и указании на него головы списка.
Посмотрите на следующую реализацию add_first() для класса LinkedList :
по определению add_first (я, узел):
узел. следующий = self.head
self.head = узел
следующий = self.head
self.head = узел
В приведенном выше примере вы устанавливаете self.head в качестве ссылки next нового узла, чтобы новый узел указывал на старый self.head . После этого нужно указать, что новый заголовок списка является вставленным узлом.
Вот как это работает с примерным списком:
>>>
>>> llist = LinkedList()
>>> список
Никто
>>> llist.add_first(Узел("b"))
>>> список
б -> Нет
>>> llist.add_first(Узел("a"))
>>> список
а -> б -> нет
Как видите, add_first() всегда добавляет узел в начало списка, даже если список до этого был пуст.
Вставка в конце
Вставка нового узла в конец списка заставляет вас сначала просмотреть весь связанный список и добавить новый узел, когда вы дойдете до конца. Вы не можете просто добавить в конец, как в обычном списке, потому что в связанном списке вы не знаете, какой узел является последним.
Вот пример реализации функции для вставки узла в конец связанного списка:
по определению add_last (я, узел):
если self.head равен None:
self.head = узел
возвращаться
для current_node в себе:
проходить
current_node.next = узел
Во-первых, вы хотите просмотреть весь список, пока не дойдете до конца (то есть до тех пор, пока цикл for не вызовет исключение StopIteration ). Затем вы хотите установить current_node в качестве последнего узла в списке. Наконец, вы хотите добавить новый узел как следующее значение этого текущий_узел .
Вот пример add_last() в действии:
>>>
>>> llist = LinkedList(["a", "b", "c", "d"])
>>> список
а -> б -> в -> г -> нет
>>> llist.add_last(Узел("e"))
>>> список
a -> b -> c -> d -> e -> нет
>>> llist.add_last(Узел("f"))
>>> список
a -> b -> c -> d -> e -> f -> нет
В приведенном выше коде вы начинаете с создания списка с четырьмя значениями ( a , b , c и d ). Затем, когда вы добавляете новые узлы с помощью
Затем, когда вы добавляете новые узлы с помощью add_last() , вы можете видеть, что узлы всегда добавляются в конец списка.
Вставка между двумя узлами
Вставка между двумя узлами добавляет еще один уровень сложности к и без того сложным вставкам связанного списка, потому что есть два разных подхода, которые вы можете использовать:
- Вставка после существующего узла
- Вставка перед существующим узлом
Может показаться странным разделять их на два метода, но связанные списки ведут себя не так, как обычные списки, и для каждого случая нужна своя реализация.
Вот метод, который добавляет узел после существующего узла с определенным значением данных:
определение add_after (я, target_node_data, new_node):
если self.head равен None:
вызвать исключение ("Список пуст")
для узла в себе:
если node.data == target_node_data:
новый_узел. следующий = узел.следующий
узел.следующий = новый_узел
возвращаться
поднять исключение ("Узел с данными "%s" не найден" % target_node_data)
следующий = узел.следующий
узел.следующий = новый_узел
возвращаться
поднять исключение ("Узел с данными "%s" не найден" % target_node_data)
В приведенном выше коде вы просматриваете связанный список в поисках узла с данными, указывающими, куда вы хотите вставить новый узел. Когда вы найдете искомый узел, вы вставите новый узел сразу после него и перемонтируете ссылку на следующий , чтобы сохранить согласованность списка.
Единственными исключениями являются случаи, когда список пуст, что делает невозможным вставку нового узла после существующего узла, или если список не содержит искомого значения. Вот несколько примеров того, как add_after() ведет себя:
>>>
>>> llist = LinkedList()
>>> llist.add_after("a", Node("b"))
Исключение: список пуст
>>> llist = LinkedList(["a", "b", "c", "d"])
>>> список
а -> б -> в -> г -> нет
>>> llist.add_after("c", Node("cc"))
>>> список
a -> b -> c -> cc -> d -> нет
>>> llist. add_after("f", узел("g"))
Исключение: узел с данными 'f' не найден
add_after("f", узел("g"))
Исключение: узел с данными 'f' не найден
Попытка использовать add_after() в пустом списке приводит к исключению. То же самое происходит, когда вы пытаетесь добавить после несуществующего узла. Все остальное работает как положено.
Теперь, если вы хотите реализовать add_before() , это будет выглядеть примерно так:
1def add_before(self, target_node_data, new_node):
2, если self.head равен None:
3 поднять исключение ("Список пуст")
4
5, если self.head.data == target_node_data:
6 вернуть self.add_first(new_node)
7
8 пред_узел = self.head
9для узла в себе:
10, если node.data == target_node_data:
11 предыдущий_узел.следующий = новый_узел
12 новый_узел.следующий = узел
13 возвращение
14 пред_узел = узел
15
16 поднять исключение ("Узел с данными "%s" не найден" % target_node_data)
Есть несколько вещей, о которых следует помнить при реализации вышеизложенного. Во-первых, как и в случае с add_after() , вы хотите создать исключение, если связанный список пуст (строка 2) или искомый узел отсутствует (строка 16).
Во-вторых, если вы пытаетесь добавить новый узел перед заголовком списка (строка 5), вы можете повторно использовать add_first() , потому что вставляемый узел будет новым заголовком списка .
Наконец, в любом другом случае (строка 9) вы должны отслеживать последний проверенный узел, используя переменную prev_node . Затем, когда вы найдете целевой узел, вы можете использовать эту переменную prev_node для переподключения значений next .
И снова пример стоит тысячи слов:
>>>
>>> llist = LinkedList()
>>> llist.add_before("a", Узел("a"))
Исключение: список пуст
>>> llist = LinkedList(["b", "c"])
>>> список
б -> в -> нет
>>> llist.add_before("b", узел("a"))
>>> список
а -> б -> в -> нет
>>> llist.add_before("b", Узел("aa"))
>>> llist.add_before("c", узел("bb"))
>>> список
a -> aa -> b -> bb -> c -> нет
>>> llist.add_before("n", узел("m"))
Исключение: узел с данными «n» не найден
С помощью add_before() теперь у вас есть все методы, необходимые для вставки узлов в любом месте списка.
Удалить рекламу
Как удалить узел
Чтобы удалить узел из связанного списка, вам сначала нужно просмотреть список, пока не найдете узел, который хотите удалить. Как только вы найдете цель, вы хотите связать ее предыдущий и следующий узлы. Это повторное связывание удаляет целевой узел из списка.
Это означает, что вам нужно отслеживать предыдущий узел при просмотре списка. Взгляните на пример реализации:
1def remove_node(self, target_node_data):
2, если self.head равен None:
3 поднять исключение ("Список пуст")
4
5, если self.head.data == target_node_data:
6 self.head = self.head.следующий
7 возврат
8
9 предыдущий_узел = self.head
10 для узла в себе:
11, если node.data == target_node_data:
12 предыдущий_узел.следующий = узел.следующий
13 возвращение
14 предыдущий_узел = узел
15
16 поднять исключение ("Узел с данными "%s" не найден" % target_node_data)
В приведенном выше коде вы сначала проверяете, что ваш список не пуст (строка 2). Если это так, то вы создаете исключение. После этого вы проверяете, является ли удаляемый узел текущей
Если это так, то вы создаете исключение. После этого вы проверяете, является ли удаляемый узел текущей головкой списка (строка 5). Если это так, то вы хотите, чтобы следующий узел в списке стал новой головкой .
Если ничего из вышеперечисленного не происходит, вы начинаете просматривать список в поисках удаляемого узла (строка 10). Если вы его найдете, вам нужно обновить его предыдущий узел, чтобы он указывал на его следующий узел, автоматически удаляя найденный узел из списка. Наконец, если вы пройдете весь список, не найдя узла, который нужно удалить (строка 16), вы вызовете исключение.
Обратите внимание, как в приведенном выше коде вы используете previous_node для отслеживания предыдущего узла. Это гарантирует, что весь процесс будет намного проще, когда вы найдете нужный узел для удаления.
Вот пример использования списка:
>>>
>>> llist = LinkedList() >>> список.remove_node("а") Исключение: список пуст >>> llist = LinkedList(["a", "b", "c", "d", "e"]) >>> список a -> b -> c -> d -> e -> нет >>> список.remove_node("а") >>> список б -> в -> г -> е -> нет >>> llist.remove_node("e") >>> список б -> в -> г -> нет >>> llist.remove_node("c") >>> список б -> г -> нет >>> список.remove_node("а") Исключение: узел с данными «a» не найден
Вот оно! Теперь вы знаете, как реализовать связанный список и все основные методы обхода, вставки и удаления узлов. Если вам комфортно с тем, что вы узнали, и вы жаждете большего, не стесняйтесь выбрать одно из испытаний ниже:
- Создайте метод для извлечения элемента из определенной позиции:
get(i)или дажеllist[i]. - Создайте метод для обращения связанного списка:
llist.reverse(). - Создайте объект
Queue(), наследующий связанный список этой статьи с помощью методовenqueue()иdequeue().
Помимо отличной практики, самостоятельные дополнительные задания — это эффективный способ усвоить все полученные знания. Если вы хотите получить фору, повторно используя весь исходный код из этой статьи, то вы можете скачать все необходимое по ссылке ниже:
Использование расширенных связанных списков
До сих пор вы знали об особом типе связанных списков, называемых односвязными списками . Но есть и другие типы связанных списков, которые можно использовать для несколько иных целей.
Как использовать двусвязные списки
Двусвязные списки отличаются от односвязных тем, что они имеют две ссылки:
- Поле
предыдущийссылается на предыдущий узел. - Поле
nextссылается на следующий узел.
Конечный результат выглядит так:
Узел (двухсвязный список) Если вы хотите реализовать описанное выше, вы можете внести некоторые изменения в существующий класс узла , чтобы включить поле предыдущего :
:
def __init__(я, данные):
self. data = данные
self.next = Нет
self.previous = Нет
data = данные
self.next = Нет
self.previous = Нет
Такая реализация позволит вам перемещаться по списку в обоих направлениях, а не только с использованием следующий . Вы можете использовать , следующий за , чтобы идти вперед, и , предыдущий , чтобы идти назад.
С точки зрения структуры двусвязный список выглядел бы так:
Двусвязный список Ранее вы узнали, что collections.deque использует связанный список как часть своей структуры данных. Это тип связанного списка, который он использует. С двусвязными списками deque может вставлять или удалять элементы с обоих концов очереди с константой О (1) производительность.
Удалить рекламу
Как использовать циклические связанные списки
Циклические связанные списки представляют собой тип связанного списка, в котором последний узел указывает на начало списка вместо указания на Нет . Это то, что делает их круглыми. Круговые связанные списки имеют довольно много интересных вариантов использования:
Это то, что делает их круглыми. Круговые связанные списки имеют довольно много интересных вариантов использования:
- Обход хода каждого игрока в многопользовательской игре
- Управление жизненным циклом приложений данной операционной системы
- Реализация кучи Фибоначчи
Вот как выглядит круговой связанный список:
Циклический связанный список Одним из преимуществ циклических связанных списков является то, что вы можете просмотреть весь список, начиная с любого узла. Поскольку последний узел указывает на головку списка, вам нужно убедиться, что вы остановите обход, когда достигнете начальной точки. В противном случае вы попадете в бесконечный цикл.
С точки зрения реализации циклические связанные списки очень похожи на односвязные списки. Единственное отличие состоит в том, что вы можете определить начальную точку при обходе списка:
класс CircularLinkedList:
защита __init__(сам):
self. head = Нет
def traverse(я, start_point=None):
если начальная_точка равна None:
начальная_точка = self.head
узел = начальная_точка
в то время как node не None и (node.next! = начальная_точка):
узел выхода
узел = узел.следующий
узел выхода
def print_list (я, start_point = None):
узлы = []
для узла в self.traverse(starting_point):
узлы.append (ул (узел))
print(" -> ".join(узлы))
head = Нет
def traverse(я, start_point=None):
если начальная_точка равна None:
начальная_точка = self.head
узел = начальная_точка
в то время как node не None и (node.next! = начальная_точка):
узел выхода
узел = узел.следующий
узел выхода
def print_list (я, start_point = None):
узлы = []
для узла в self.traverse(starting_point):
узлы.append (ул (узел))
print(" -> ".join(узлы))
Обход списка теперь получает дополнительный аргумент, начальная_точка , который используется для определения начала и (поскольку список циклический) конца процесса итерации. Кроме того, большая часть кода такая же, как и в нашем классе LinkedList .
Чтобы завершить последний пример, посмотрите, как этот новый тип списка ведет себя, когда вы вводите в него некоторые данные:
>>>
>>> circular_llist = CircularLinkedList() >>> round_llist.print_list() Никто >>> а = узел ("а") >>> b = узел ("b") >>> с = узел ("с") >>> d = узел ("d") >>> а.следующий = б >>> б.следующий = с >>> c.next = d >>> д.след = а >>> round_llist.head = а >>> round_llist.print_list() а -> б -> в -> г >>> round_llist.print_list(b) б -> в -> г -> а >>> round_llist.print_list(d) г -> а -> б -> в
Вот оно! Вы заметите, что у вас больше нет None при просмотре списка. Это потому, что у кругового списка нет определенного конца. Вы также можете видеть, что выбор разных начальных узлов приведет к немного разным представлениям одного и того же списка.
Заключение
Из этой статьи вы узнали немало вещей! Самые важные из них:
- Что такое связанные списки и когда их следует использовать
- Как использовать
collections.dequeдля реализации очередей и стеков - Как реализовать собственный связанный список и классы узлов, а также соответствующие методы
- Какие существуют другие типы связанных списков и для чего их можно использовать
Если вы хотите узнать больше о связанных списках, ознакомьтесь с постом Вайдехи Джоши на Medium, где вы найдете хорошее наглядное объяснение. Если вас интересует более подробное руководство, то статья в Википедии достаточно подробная. Наконец, если вам интересны причины текущей реализации
Если вас интересует более подробное руководство, то статья в Википедии достаточно подробная. Наконец, если вам интересны причины текущей реализации collections.deque , затем загляните в ветку Рэймонда Хеттингера.
Вы можете загрузить исходный код, используемый в этом руководстве, нажав на следующую ссылку:
Не стесняйтесь оставлять любые вопросы или комментарии ниже. Удачного питона!
Смотреть сейчас Это руководство содержит связанный с ним видеокурс, созданный командой Real Python. Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Работа со связанными списками в Python
Понимание структур данных: связанные списки | Rylan Bauermeister
Это руководство предназначено для ознакомления со структурой данных связанного списка. Он будет охватывать саму структуру, ее вычислительные тайминги, ее общие алгоритмы и то, как кодировать ее различные перестановки.
Содержащиеся здесь примеры написаны на Javascript исключительно по желанию автора, но написаны специально для того, чтобы быть доступными для других языков программирования.
Многие считают, что связанные списки являются самой простой структурой данных, и легко понять, почему. Связанный список состоит из серии из узлов , каждый из которых содержит указатель на следующий узел в ряду. Обычно это завершается узлом, который указывает на null , что означает конец списка. Визуально это выглядит примерно так:
Первая ошибка, которую совершают многие люди, глядя на связанный список, состоит в том, что они предполагают, что это странная реализация массива. Хотя эти две структуры имеют много поверхностного сходства, это сходство лишь внешнее. Эти двое различные способы хранения связанных данных .
Давайте рассмотрим, чем связный список отличается от массива, а именно способом хранения в памяти.
Массив занимает блок памяти. В строгих языках, таких как Java или Rust, этот размер должен быть указан заранее, и поэтому они занимают выделенный кусок памяти, равный количеству элементов, умноженному на размер типа данных. В динамических языках, таких как Javascript, массивы можно увеличивать или уменьшать в соответствии с потребностями программиста. В обоих случаях они хранятся в памяти как массив данных. Вы можете получить доступ к следующему элементу в массиве, переместившись вперед на N байтов, где N — размер сохраняемого элемента. Таким образом, вы можете достичь индекса X, переместив вперед NX байтов.
В динамических языках, таких как Javascript, массивы можно увеличивать или уменьшать в соответствии с потребностями программиста. В обоих случаях они хранятся в памяти как массив данных. Вы можете получить доступ к следующему элементу в массиве, переместившись вперед на N байтов, где N — размер сохраняемого элемента. Таким образом, вы можете достичь индекса X, переместив вперед NX байтов.
Связанные списки, с другой стороны, могут быть распределены в памяти. Хотя это усложняет доступ к определенному узлу, зато значительно ускоряет создание новых узлов и удаление старых, поскольку они могут быть созданы в любом месте памяти. Атрибут next узла связанного списка содержит указатель на память, в которой хранится следующий узел.
Если у вас возникли проблемы с отличением связанных списков от массивов, это должно помочь. Вы сразу же заметите, что массивы и связанные списки являются полярными противоположностями с точки зрения времени. Причина проста: поскольку связанные списки не привязаны к одному месту в памяти, они могут очень легко вставлять новое содержимое в начале (или 9).0278 глава) перечня. Однако добавление в конец списка требует обхода всего списка, поскольку базовый связанный список не хранит количество содержащихся в нем элементов.
Причина проста: поскольку связанные списки не привязаны к одному месту в памяти, они могут очень легко вставлять новое содержимое в начале (или 9).0278 глава) перечня. Однако добавление в конец списка требует обхода всего списка, поскольку базовый связанный список не хранит количество содержащихся в нем элементов.
ПРИМЕЧАНИЕ. другие типы связанных списков сохраняют эту информацию. Дополнительные сведения см. в разделе «Связанный список с хвостом и размером» в конце этого руководства.
То же самое относится и к чтению: для доступа к N-му элементу в связанном списке требуется пройти N элементов.
С помощью массива легко получить доступ к концу списка, но манипулировать серединой или началом сложно. Поскольку он занимает определенное место в памяти, для вставки или удаления из любого места, кроме начала списка, требуется сдвиг всей остальной части списка вперед. Если вы вставляете новые данные в индекс 1, вам нужно переместить то, что было раньше, в индекс 2. Затем вам нужно скорректировать индекс 2 вперед до 3, и так далее, и так далее до конца массива.
Затем вам нужно скорректировать индекс 2 вперед до 3, и так далее, и так далее до конца массива.
В связанных списках старый узел можно просто удалить, например:
Рис. 3. Удаление узла в связанном списке Указатель с узла 1 на узел 2 перезаписывается, чтобы указывать на узел 3 вместо этого . Ничего не нужно перемещать, потому что место хранения данных в памяти не имеет значения.
Ответ: много мест! Возможность расширения связанных списков без существенного воздействия на память делает их очень полезными структурами. Несколько мест, где они сияют:
- Стеки и очереди : поскольку эти две структуры данных не заботятся о данных в середине массива, а только о его концах, связанные списки могут использоваться для создания чрезвычайно эффективной версии обоих.
- Любой случай, когда важны только соседние узлы : представьте слайд-шоу. У вас есть следующая кнопка и предыдущая кнопка. Связанный список был бы совершенно эффективным способом хранения этой информации, когда вам нужно будет только извлечь соседний фрагмент данных, что можно сделать очень быстро.
 То же самое можно сказать о музыкальных проигрывателях или истории веб-браузера.
То же самое можно сказать о музыкальных проигрывателях или истории веб-браузера. - Вам нужен массив, но вы планируете много вставлять и мало читать : если у вас есть знания о применении структуры данных до того, как вы начнете, это позволит вам сделать гораздо более оптимальный выбор. В этом случае, если вы знаете, что вам нужно хранить данные, но будете вставлять в них элементы чаще, чем вам нужно извлекать из них один элемент, то связанный список может прекрасно удовлетворить ваши потребности.
Как и во многих аспектах программирования, хитрость в том, чтобы узнать, когда применять структуру, заключается в тщательном рассмотрении ситуации, в которой она используется, с последующим анализом того, как плюсы и минусы каждой структуры могут быть использованы для удовлетворить ваши потребности. Связанные списки кажутся странной маленькой структурой, но на самом деле у них много потенциальных применений.
Чтобы эффективно работать со связанными списками, есть пара алгоритмов (используя этот термин в широком смысле), которые программист должен держать в своем заднем кармане. Давайте рассмотрим их.
Давайте рассмотрим их.
Обход связанного списка
Связанные списки чаще всего перебираются с использованием цикла while . Поскольку у них нет индексов, циклы для на самом деле не очень полезны. Вместо этого мы перемещаемся по ним, проверяя, равен ли текущий узел (или его указатель next ) ноль .
Вот базовая функция печати:
Рис. 4: перебор связанного списка Эта функция перемещается по связанному списку и печатает значение в каждой позиции. Переменная read неоднократно устанавливается в собственное свойство next , перемещая ее вниз по строке, пока она не станет равной null (и, следовательно, не достигнет конца списка). Обратите внимание, что мы делаем , а не используем значение для головы, а вместо этого назначаем новую переменную; если бы мы переназначили head , мы потенциально можем потерять его и уничтожить весь список. На сегодняшний день лучше использовать вторичную переменную.
Удаление значения
Допустим, вы хотите удалить значение 2 из связанного списка. Вам нужно будет перебрать список, просматривая один узел вперед, пока не найдете узел, содержащий 2 . Затем вы захотите сшить текущий узел с узлом на два впереди него (или нулевым, в зависимости от случая), как показано на рис. 3.
Строки 2–8 охватывают крайние случаи. Первый проверяет, что список содержит что-либо. Если это не так, мы возвращаем -1 , признак того, что мы не нашли рассматриваемое значение. Вторая проверка гарантирует, что значение, которое мы пытаемся удалить, не является значением самой головы. Если это так, мы просто удаляем текущую голову, устанавливая this.head на this.head.next .
В остальном используется базовый обход, как показано на рис. 4, только вместо просмотра текущего узла мы смотрим на следующий узел. Когда мы находим нашу цель, мы устанавливаем read. на  next
next read.next.next , эффективно пропуская узел, содержащий значение, которое мы хотели удалить. Мы можем гарантировать, что read.next.next является действительной переменной, потому что наш цикл проверяет, что read.next инициализировано.
Обнаружение цикла
Еще одна распространенная проблема, которая может возникнуть в связанных списках, — это цикл (или цикл ). Рассмотрим следующее:
Рис. 6: Циклический список Это, очевидно, проблема. Если мы используем проверку на null , чтобы определить, следует ли остановить цикл, этот список вызовет ошибку наших предыдущих функций. Хотя хорошо составленный связанный список никогда не позволит программисту войти в это состояние, совершенно необходимо знать, как его проверять.
Алгоритм, который обычно используется, в просторечии называется черепаха и заяц метод обнаружения циклов. Он проверяет наличие циклов, запуская два указателя, один из которых движется с удвоенной скоростью, чем другой. Если они когда-либо указывают на одно и то же, мы знаем, что список имеет цикл. Если, с другой стороны, любой из них когда-либо достигает нуля, мы знаем, что список заканчивается естественным образом.
Если они когда-либо указывают на одно и то же, мы знаем, что список имеет цикл. Если, с другой стороны, любой из них когда-либо достигает нуля, мы знаем, что список заканчивается естественным образом.
Вот реализация:
Рис. 7. Обнаружение цикла черепахи и зайца Первое, что мы делаем для этого алгоритма, — это проверяем первые три позиции на наличие null . Очевидно, что если какой-либо из них равен null , мы знаем, что наш список заканчивается естественным образом. Потом мы их отключили. Мы проверяем только hare 's .next на нуль, так как Tort будет отставать; любое полученное значение уже будет проверено зайцем . Если в какой-то момент они строго равны друг другу, мы знаем, что нашли цикл.
ПРИМЕЧАНИЕ. вас могут интересовать повторяющиеся значения. Изучите алгоритм, и вы обнаружите, что мы на самом деле никогда не проверяем значение, содержащееся в узлах, — мы только проверяем, равны ли сами узлы.
В Javascript для этого требуется, чтобы объекты были на самом деле одинаковыми, то есть хранились в одном и том же слоте памяти. Таким образом, мы можем проверять наличие циклов в списках, содержащих повторяющиеся значения.
В этом разделе мы рассмотрим три основные формы связанных списков.
Односвязный списокКаждый связанный список начинается с класса узла. Вот один из них:
Рис. 8: класс Node Это говорит само за себя. Это небольшая структура данных, содержащая конструктор, который принимает значение и сохраняет его в val. Он также выделяет место для свойства next .
ПРИМЕЧАНИЕ. , так как мы работаем на Javascript, часть того, что мы здесь программируем, является избыточным. JS не требует выделения места; вы можете присвоить переменным дополнительные свойства, когда захотите. Это, однако, представляет форму, которую это примет во многих других языках. Хотя это руководство написано на JS, оно предназначено для людей, использующих любой язык.
Теперь, когда у нас есть класс Node, нам нужен связанный список. Оболочка для наших функций будет выглядеть примерно так:
Рис. 9: оболочка для класса Linked List Можно предположить, что весь будущий код будет существовать внутри этой оболочки, в указанной области. Здесь нет ничего примечательного, за исключением инициализации переменной head, которая в настоящее время имеет значение null (поскольку список пуст).
Давайте придадим этой штуке немного больше твердости, внедрив push и извлекают , чтобы мы могли редактировать конец списка.
Давайте начнем с обсуждения нажмите . Впереди есть базовая проверка, которая проверяет, пуст ли список; если это так, мы просто назначаем this.head новому узлу со значением val . В противном случае нам нужно найти конец списка, а затем присвоить нашему новому узлу .next предыдущего конечного узла.
pop немного сложнее. Как с push , мы выделяем немного места для проверки ошибок. Строки 18–23 посвящены закрытию крайних случаев. Что становится интересным, так это строка 27.
Вы заметите, что на этот раз мы проверяем read.next.next . Это потому, что нам нужен предпоследний узел . Когда read.next.next === null , мы будем знать, что находимся на предпоследнем узле в списке. Затем все, что нам нужно сделать, это установить для read.next значение null, что указывает на то, что мы вырезали последний элемент списка.
Здесь есть небольшая дополнительная логика, связанная с возвращаемым значением, которое здесь называется ret . Это просто для отражения поведения массива. Когда узел извлекается, мы возвращаем его значение. Такое поведение будет существовать в аналогичных функциях и будущих итерациях этой, так что не пугайтесь.
shift и unshift гораздо короче:
 11: shift и unshift
11: shift и unshift Поскольку у нас уже есть доступ к head , мы точно знаем, куда поместим новый узел. В shift мы делаем быструю проверку ошибок, чтобы убедиться, что мы не сдвигаем пустой список, затем просто устанавливаем this.head на this.head.next .
unshift не намного сложнее. Мы создаем новый узел со значением next равным this.head . Затем мы повторно объявляем this.head равным нашему новому узлу. Легкий!
Здесь можно использовать функцию удаления , показанную на рис. 5, а также функцию печати . Последняя функция, которую нужно записать, — это простая содержит . Эта функция очень проста и может быть представлена без лишних слов:
Мы используем нашу базовую итерацию цикла while, сравниваем значение каждого узла со значением, которое мы получили в качестве аргумента. Если находим, возвращаем true. В противном случае верните ложь.
В противном случае верните ложь.
Связанный список с хвостом и размером
К этому моменту вы достаточно хорошо разберетесь со структурой и даже запрограммируете свой собственный список. Возможно, вы начинаете задаваться вопросом: почему так сложно получить доступ к концу списка? Почему мы не отслеживаем размер списка?
Ответ прост: мы не были, потому что это было проще. Тем не менее, вы можете, и многие люди делают! Очень мало в программировании высечено на камне. Внесение изменений в варианты использования часто является полезным или даже ожидаемым талантом. Итак, давайте посмотрим, как будут выглядеть некоторые из этих функций, если мы попытаемся реализовать голову и хвост.
Для начала нужно изменить наш конструктор.
Рис. 13: конструктор связанного списка с началом и хвостом.Есть. Теперь мы инициализируем связанный список, чтобы он имел нулевой размер и хвост, равный его начальной голове.
Обновление push и pop идет дальше.
push стало намного проще! Помимо проверки крайних случаев в строках 4–7, мы видим, что вся операция теперь может быть выполнена в 3 строки и за время O (1). Это большой толчок! Все, что нам нужно сделать, это установить tail.next в новый узел, содержащий переданное значение, а затем увеличить размер.
pop , с другой стороны, получился немного корявым. Строки 17–23 — все проверки ошибок (если вам интересно, вы можете увидеть полный код вспомогательной функции 9).0214 returnHeadAndClear() ). Однако то, что будет дальше, кажется слишком сложным! Разве мы сейчас не сохраняем хвостовое значение? Что это?
Ну, для того, чтобы установить новый хвост, нам нужен предпоследний элемент в связанном списке. Это означает повторный обход всего списка, так как наш список содержит указатели, идущие в одном направлении. Эту проблему можно исправить, и она будет рассмотрена в следующем разделе, , двусвязные списки.
Остальной код очень похож, за исключением увеличения и уменьшения счетчика размера. Эта новая версия кажется отличной, но неспособность двигаться в другом направлении раздражает. Давайте посмотрим, как это исправить.
Двусвязные списки
Ранее мы кодировали односвязных списков . Под этим подразумевается, что указатели текут только в одном направлении. Узлы имеют свойство следующий , но не свойство предыдущий . Список, который течет в обоих направлениях, можно назвать двусвязным.
Давайте посмотрим на реализацию.
Рис. 15: двусторонний узел Для начала у нас есть двусторонний узел. У него есть и , и следующий , и свойство предыдущего , позволяющее двигаться в обоих направлениях. Давайте посмотрим, что это делает с нашими функциями push и pop .
Теперь это больше похоже на то, на что мы надеялись.
push выглядит аналогично, хотя теперь нам нужно присвоить значение .previous новому узлу, когда мы его нажимаем. pop , с другой стороны, стал крошечным. Все, что он делает, это присваивает хвосту значение предыдущего узла, а затем присваивает следующему узлу значение 9.0214 ноль . Именно так, как мы хотели сделать раньше, и теперь мы можем манипулировать хвостом списка за время O(1).
Другие функции почти не изменились, хотя теперь они требуют дополнительной поддержки, чтобы убедиться, что их значения предыдущего установлены правильно. Однако теперь мы можем делать такие забавные вещи, как печать списка в обратном порядке без использования вложенных циклов:
Наш связанный список теперь чертовски эффективен для очередей и стеков, и его можно читать вперед и назад. Не так уж и плохо!
Теперь у вас должно быть очень хорошее представление о том, что такое связанный список и как его можно расширить. Если вы хотите поиграть с уже написанным, посмотрите в источниках ссылку на мой репозиторий — в нем есть набор для тестирования, который вы можете использовать в дополнение к полному коду для всех этих примеров.
Если вы хотите поиграть с уже написанным, посмотрите в источниках ссылку на мой репозиторий — в нем есть набор для тестирования, который вы можете использовать в дополнение к полному коду для всех этих примеров.
RylanBauermeister/linked-list-demo
Внесите свой вклад в разработку RylanBauermeister/linked-list-demo, создав учетную запись на GitHub.
github.com
Применение структуры данных связанного списка — GeeksforGeeks
Связанный список представляет собой линейную структуру данных, в которой элементы не хранятся в смежных ячейках памяти. The…
www.geeksforgeeks.org
Генератор HTML-таблиц — TablesGenerator.com
Бесплатный и простой в использовании онлайн-генератор HTML-таблиц — введите данные таблицы и просто скопируйте и вставьте сгенерированную таблицу…
www .tablesgenerator.com
Sketch.IO — Создатель Sketchpad
Sketchpad доступен в Интернете и для загрузки на ПК и Mac.
 Работаете ли вы над школьным плакатом или…
Работаете ли вы над школьным плакатом или…sketch.io
Связанные списки | Руководства по CodePath Cliffnotes
Введение
Начнем с примера очень важного связанного списка. Для любой работающей программы наиболее фундаментальной структурой, объясняющей состояние программы в любой момент времени, является стек вызовов. Если вы сталкивались с неприятной ошибкой во время выполнения, вы могли бы подтвердить это. Например, вот изображение стека вызовов во время отладки в браузере Chrome.
Стек вызовов — это просто трассировка от текущего положения программы до начала этого процесса или потока. Этот простой след домой необходим для того, чтобы компьютер знал, что делать, когда текущая функция, над которой он работает, завершается. В этом случае компьютер знает, что он может просто перейти к первому элементу в этом стеке, удалить его из списка, сделать второй элемент теперь первым в стеке, а затем выполнить остальную работу, которую выполнял предыдущий первый элемент. указывая на. Эта последовательность из одного элемента (адреса в памяти), указывающего на другой элемент (адрес в памяти), указывающего на другой элемент, и так далее, образует связанный список.
указывая на. Эта последовательность из одного элемента (адреса в памяти), указывающего на другой элемент (адрес в памяти), указывающего на другой элемент, и так далее, образует связанный список.
Наиболее распространенные варианты связанных списков:
- Односвязный список
- Двусвязный список
- Циклический связанный список
Все варианты относятся к тому, как элементы ( узлов ) списка указывают друг на друга. Односвязный список будет иметь только один указатель, который имеет ссылку на следующий узел в списке, тогда как двусвязный список будет иметь указатель на следующий элемент, а также на предыдущий элемент. Практически во ВСЕХ сценариях проведения собеседований связанным списком будет односвязный список, а остальная часть документации будет ссылаться на связанный список как на этот и только на другие типы списков, если они упоминаются отдельно.
Минимальное, но довольно распространенное определение узла связанного списка в Python:
class ListNode:
защита __init__(я, значение):
self. val = значение
self.next = Нет
val = значение
self.next = Нет Где,
голова = узел списка (1) head.next = СписокУзел(2)
, создаст список 1 -> 2 и 1 в начале списка.
Плюсы и минусы
Если мы подумаем о примере со стеком вызовов, мы действительно работали только с одной стороной (головой) списка. Наши операции состояли из 1) перехода к началу списка, чтобы найти следующую функцию, которую требовалось запустить нашему процессу, и 2) добавления новой функции в начало списка и указания узла, содержащего эту функцию, на вершину списка. предыдущая глава.
Связанные списки действительно хороши, когда мы ограничиваем наши операции одним концом структуры данных, а также имеем дело с произвольными, но небольшими размерами (количеством узлов списка). Связный список — хороший выбор в этом случае, потому что с ним просто работать и он эффективен.
Списки плохо работают, если вы хотите поддерживать произвольный доступ, т. е. работать в любом произвольном месте в списке. Это связано с тем, что единственный способ добраться до конца списка — это переходить по одному узлу за раз, запрашивая следующий элемент вниз, пока вы не достигнете желаемого местоположения.
е. работать в любом произвольном месте в списке. Это связано с тем, что единственный способ добраться до конца списка — это переходить по одному узлу за раз, запрашивая следующий элемент вниз, пока вы не достигнете желаемого местоположения.
Нам также не нравится хранить большие объемы информации в связанных списках, потому что за каждое значение, которое вы сохраняете, вы платите дополнительный штраф за хранение объекта Node, который украшает элемент, который вы хотите сохранить. Подытожим компромиссы сложности следующим образом:
Сложность во времени и пространстве
Лучшие случаи: Доступ/поиск: O(1) Вставка в головке: O(1) Удаление в начале: O(1)
Наихудшие случаи: Доступ/Поиск: О(Н) Вставка: О(Н) Удаление: O(N)
Лучший случай возникает, когда узел находится во главе списка, а Худший случай — когда узел находится в конце списка.

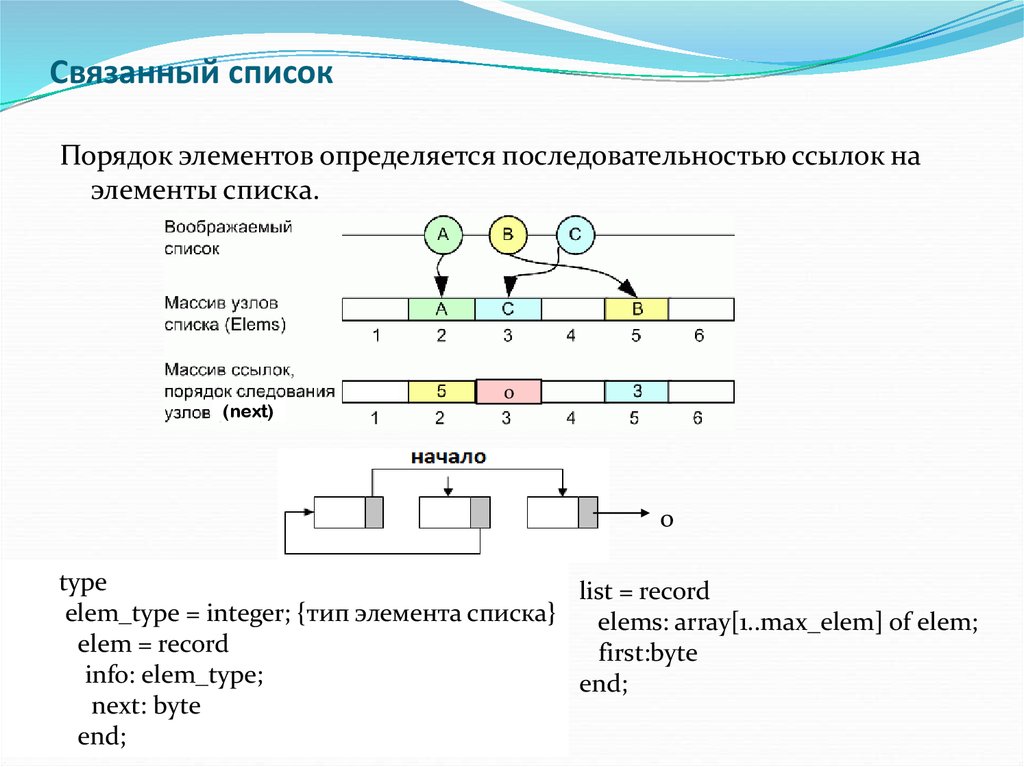 nextnode = None # Initialize next as null
a = Node(1) # declaring data in each node
b = Node(2)
c = Node(3)
a.nextnode = b # link first node to second node
b.nextnode = c # link second node to third node
a.next.value # will return the value of the next node b = 2
nextnode = None # Initialize next as null
a = Node(1) # declaring data in each node
b = Node(2)
c = Node(3)
a.nextnode = b # link first node to second node
b.nextnode = c # link second node to third node
a.next.value # will return the value of the next node b = 2
 data = None # container of the data
self.next_node = None # standard pointer to next node
self.prev_node = None # pointer to previous node
# Creating each node
a = Node(1)
b = Node(2)
c = Node(3)
# Connect the nodes
# Connect nodes a & b to each other in both directions
a.next_node = b
b.prev_node = a
# Connect nodes b & c to each other in both directions
b.next_node = c
c.prev_node = b
"""
We could create a circularly linked list by connecting the head of the list
to the tail
"""
data = None # container of the data
self.next_node = None # standard pointer to next node
self.prev_node = None # pointer to previous node
# Creating each node
a = Node(1)
b = Node(2)
c = Node(3)
# Connect the nodes
# Connect nodes a & b to each other in both directions
a.next_node = b
b.prev_node = a
# Connect nodes b & c to each other in both directions
b.next_node = c
c.prev_node = b
"""
We could create a circularly linked list by connecting the head of the list
to the tail
"""
 nextnode:
raise LookupError('Error: Command continues past index of list')
# if not edge case, move the right pointer to next node
pointer_1 = pointer_1.nextnode
# now there is a n-size block between them
# as long as the right pointer does not reach the end of the list
# the left pointer will move
while pointer_1.nextnode:
# once the right pointer hits the end the left pointer has found the
# nth to last node from the end
pointer_2 = pointer_2.nextnode
pointer_1 = pointer_1.nextnode
# return the nth to last node
return pointer_2
nextnode:
raise LookupError('Error: Command continues past index of list')
# if not edge case, move the right pointer to next node
pointer_1 = pointer_1.nextnode
# now there is a n-size block between them
# as long as the right pointer does not reach the end of the list
# the left pointer will move
while pointer_1.nextnode:
# once the right pointer hits the end the left pointer has found the
# nth to last node from the end
pointer_2 = pointer_2.nextnode
pointer_1 = pointer_1.nextnode
# return the nth to last node
return pointer_2
 cargo = cargo
self.next = next
def __str__(self):
return str(self.cargo)
cargo = cargo
self.next = next
def __str__(self):
return str(self.cargo)
 next
print_backward(tail)
print head,
next
print_backward(tail)
print head,
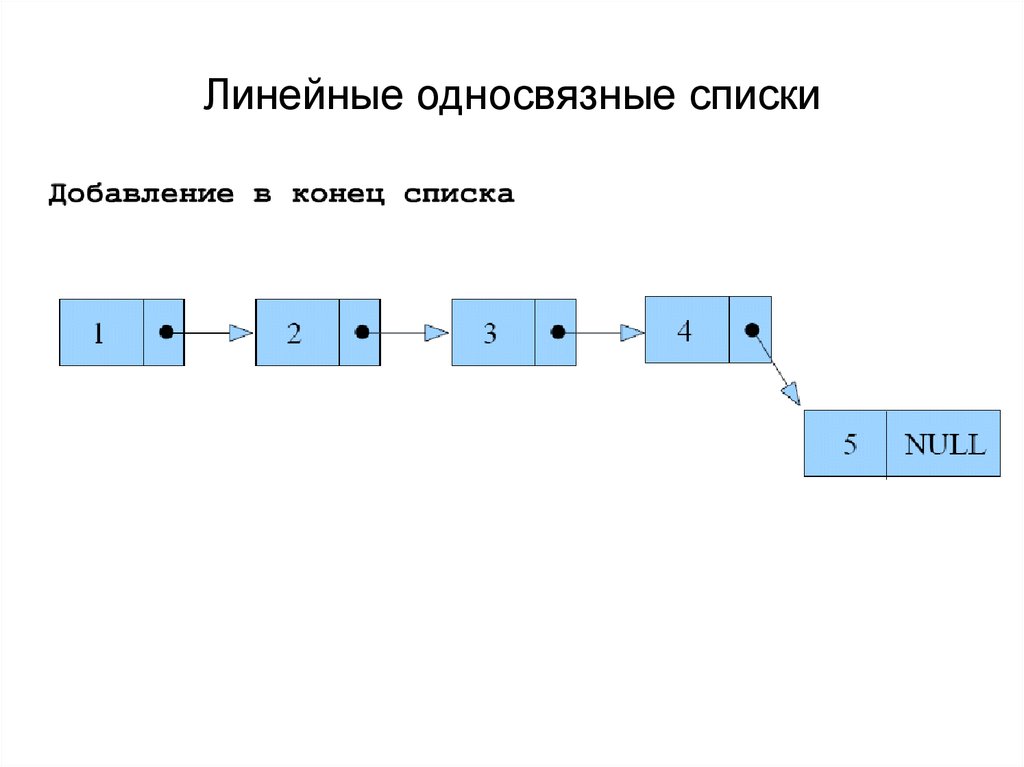 next
# make the first node refer to the third
first.next = second.next
# separate the second node from the rest of the list
second.next = None
return second
next
# make the first node refer to the third
first.next = second.next
# separate the second node from the rest of the list
second.next = None
return second
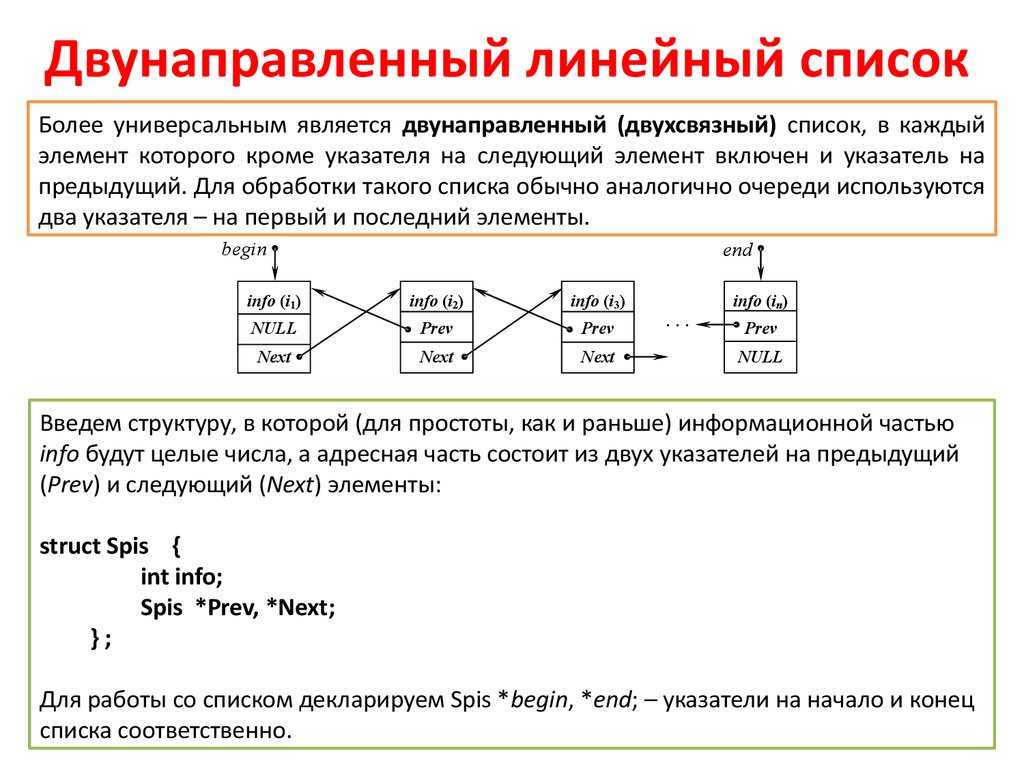 ..
def print_backward(self):
print "[",
if self.head != None:
self.head.print_backward()
print "]",
class Node:
...
def print_backward(self):
if self.next != None:
tail = self.next
tail.print_backward()
print self.cargo,
..
def print_backward(self):
print "[",
if self.head != None:
self.head.print_backward()
print "]",
class Node:
...
def print_backward(self):
if self.next != None:
tail = self.next
tail.print_backward()
print self.cargo,
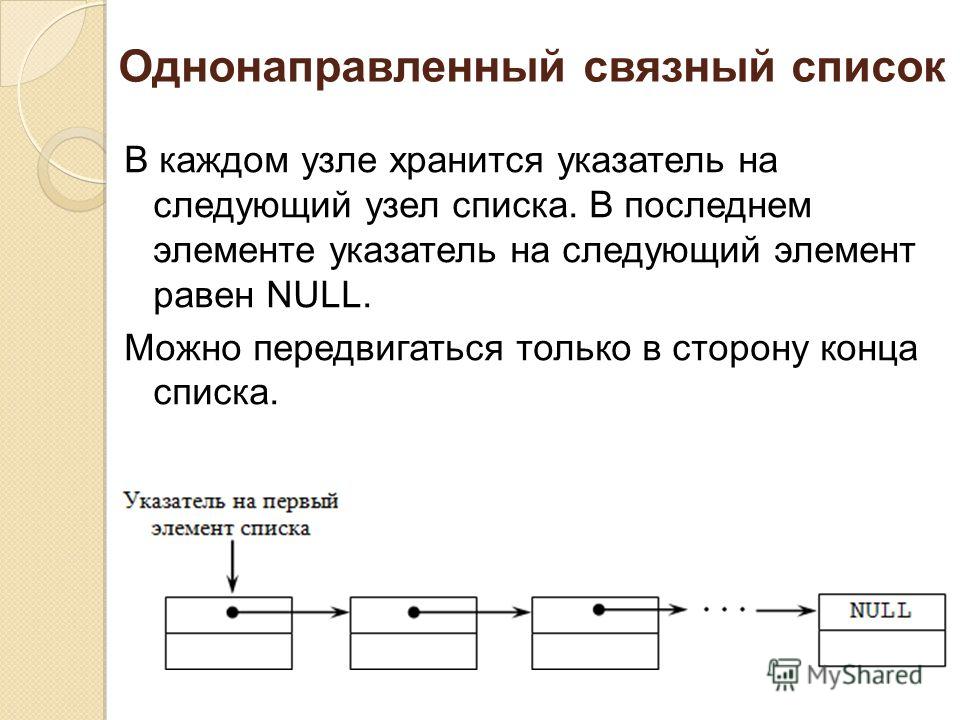 head = node
self.length += 1
head = node
self.length += 1

 Протестируйте работу метода для пустого и непустого списков.
Протестируйте работу метода для пустого и непустого списков. 2)
node3 = ListNode("Berlin")
2)
node3 = ListNode("Berlin")
 next
return count
next
return count
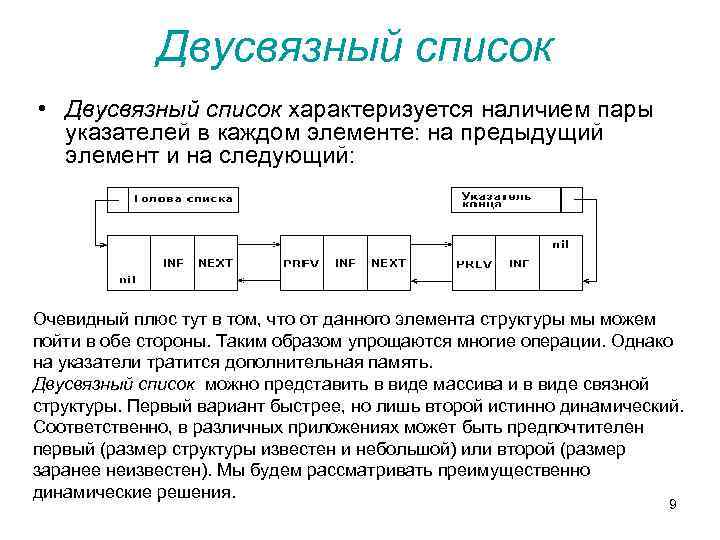 py
track length: 0
track length: 1
15
track length: 2
15
8.2
track length: 3
15
8.2
Berlin
track length: 4
15
8.2
Berlin
15
py
track length: 0
track length: 1
15
track length: 2
15
8.2
track length: 3
15
8.2
Berlin
track length: 4
15
8.2
Berlin
15